【转载】 无穷小与高阶

无穷小与高阶

注：此为转载文章。为增加可读性作了恰当修改。仅供学习参考。原文来自：
tetradecane
https://zhuanlan.zhihu.com/p/516545395
上海交通大学 工学硕士在读

学习阶段：大学数学。

前置知识：函数极限、无穷小的比较。

本文对于一些关于无穷小的概念的解读，可能是高数教材中或课程中没有出现过的，但是对于理解这些概念很有帮助。

1. 无穷小是函数

无穷小是什么？

无穷小（无穷小量，infinitesimal）是函数，且，这个函数$ f(x) $有这样一个特性：

注：数列也算是特殊的函数。

当自变量 \(x\) 趋于某个常数或无穷大时(记为\(x \to \square\))，函数值f(x)趋于0。即：

\[\lim\limits_{x\to \square}f(x)=0 \]

因此，无穷小的完整说法应该是：

\(x \to \square\) 时的无穷小

当这个自变量的极限过程 \(x \to \square\) 不言自明，不必特意指出时，我们简称$ f(x) $为无穷小。
例如：

$x\over x^2+1 $ 是 \(x \to 0\) 时和 \(x \to \infty\) 时的无穷小，但不是 \(x \to 1\) 时的无穷小。

很多地方会用希腊字母函数来表记无穷小 $ \alpha(x) $ 和 $ \beta(x) $. 甚至当自变量 \(x\) 也不必特意指出的时候，将它们简记为 \(\alpha\) 和 $ \beta $。

但是一定要记住：无穷小仍然是函数，而且涉及到自变量的一个极限过程。

2. 高阶

比较无穷小时，我们一般默认自变量需要有相同的极限过程 \(x \to \square\) 并有时将其省略。

通常，教材上只会给出如下高阶的定义：

当 \(\alpha\) 与 $ \beta $ 均为无穷小时，若 $ \lim\limits_{x\to \square}{\beta \over \alpha}=0 $ ，则称 $ \beta $ 是 \(\alpha\) 的高阶，记为 $ \beta=o(\alpha)$ ，同时称 \(\alpha\) 是 \(\beta\) 的低阶无穷小。

不知你有没有注意到，记号$ \beta=o(\alpha)$ 不能交换过来写为 $ o(\alpha)=\beta$ 。
例如:

\[x^2+x^3 = o(x) \]

是成立的，但不能写:

\[o(x) = x^2+x^3 \]

因此，这里的等于号 \(=\) 不是一般意义上的等于号，是有方向的。

我们可以把高阶，通常又称函数集合为函数族（family of functions），即将\(o(\alpha)\) 视为：

\[\{\gamma|\lim\limits_{x\to\square}\frac{\gamma}{\alpha}=0\} \]

这样的话，记号 \(\beta= o(\alpha)\) 可以理解为元素属于集合的关系，即:

\[\beta \in o(\alpha ) \]

同时，单一函数 \(\beta\) 又可视为一个单元素函数族，即 \(\{\beta\}\)，那么记号 \(\beta= o(\alpha)\) 又可以理解为集合包含于集合的关系，即:

\[\{\beta\} \subseteq o(\alpha ) \]

实际上，我们一般会推广一下：
若

\[\lim_{x\to\square}\frac\gamma f= 0 \]

均可记为

\[\gamma =o(f) \]

此时函数 \(f\) 不一定是无穷小。因此

\[o(1)=\left\{\gamma\left|\lim_{x\to\square}{\gamma\over 1}=0\right.\right\} \]

是所有无穷小的集合。

另外，若A是一个函数族，则o(A)也是个函数族，定义

\[o(A)=\left\{\alpha\left|\forall f\in A,\lim\frac\alpha f=0\right.\right\} \]

，即比A中所有函数都要高阶的无穷小的集合。

如果 $ o(\alpha)=o(\beta) $ 且 $ o(\beta)=o(\alpha) $ ，即这两个集合是相等的，为了表示区别，本文记为 $ o(\alpha)\equiv o(\beta) $ 。

3. 小o记号的运算

3.1 运算的定义

小o记号是可以进行数学运算的，例如：

\[\begin{align*} x+o(x)&=\{x\}+o(x)\\ &=\left\{x+\alpha\left|\lim\frac\alpha x=0\right.\right\} \end{align*} \]

\[o(x)+o(x^2)=\left\{\alpha+\beta\left|\lim\frac\alpha x=0,\lim\frac\beta{x^2}=0\right.\right\} \]

注意到：上述 $ x+o(x) $ 和 $ o(x)+o(x^2) $ 中的加号也不是一般意义上集合的并集，而是在函数族上定义的一种特殊运算，即集合中元素的运算：

\[A+B=\{f+g|f\in A,g\in B\} \]

其他运算也是同理。

3.2 运算律

小o记号的运算律如下所示：

1. 数乘律：若k为非零常数，则

\[\begin{align*} ko(f) &\equiv o(kf)\\ &\equiv o(f) \end{align*} \]

2. 加减律： $ o(f)\pm o(g)=o(|f|+|g|) $ .
   若 $ g=o(f) $ 或 $ g\sim f $ ，则 $ o(|f|+|g|)=o(f) $ .
3. 乘法律： $ o(f)\equiv fo(1) $ , $ ~o(f)o(g)=o(fg)\equiv fo(g)\equiv fgo(1) $ .
4. 乘方律：若k为正整数，则 $ (o(f))^k = o(f^k) $ .

以下思想在用泰勒展开计算函数极限时非常有用：

由数乘律知，小o记号中的数乘可直接略去。
由加减律知，小o记号中的无穷小会被不高阶于它的函数吸收掉。
由乘法律知，小o记号中的因式可以提到外面来，但至少要留一个小o记号。

4. 小o记号的例子

将高阶无穷小视为函数族后，我们就更容易理解很多高阶无穷小的关系和极限运算了。

例如：

$ o(x)=o(1) $ 是对的，因为 $ o(x)\subsetneq o(1) $ ， $ x $ 的所有高阶无穷小都是无穷小，而不能写 $ o(1)=o(x) $ ，例如x就是一个反例，因为 $ x\in o(1) $ 但 $ x\notin o(x) $ .

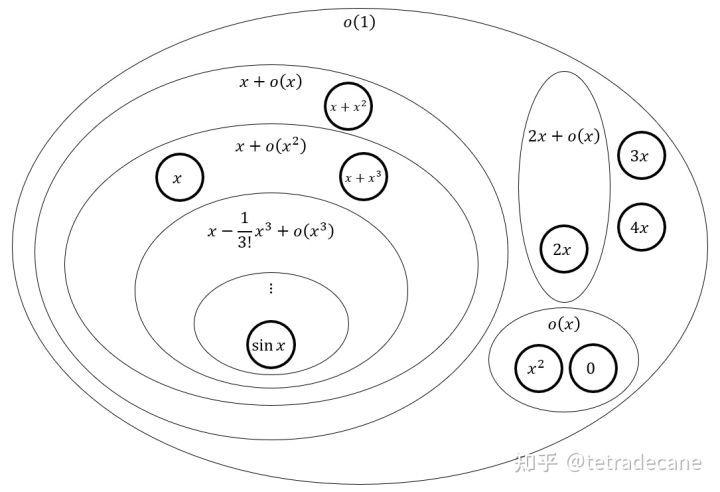
泰勒展开式 $ \sin x=x+o(x) $ 是对的，同时 $ \sin x=x+o(x^2) $ 也是对的，这是因为

\[\{\sin x\}\subsetneq x+o(x^2)\subsetneq x+o(x) \]

实际上 $ x+o(x^2) $ 是更小的集合，精度更高，泰勒展开多展了一阶，展开到了 $ x^2 $ ，只不过 $ x^2 $ 的系数恰好为0，也就是相当于 $ \sin x=x+0x^2+o(x2) $ .

又如极限运算：

\[\begin{align} \lim_{x\to0}\frac{x-\sin x} {x^3}&=\lim_{x\to0}\frac{x-\left(x-\frac1{3!}x^3+o(x^3)\right)} {x^3}\\ &=\lim_{x\to0}\frac{\frac16x^3+o(x^3)} {x^3}\\ &=\frac16+\lim_{x\to0}\frac{o(x^3)} {x^3}\\ &=\frac16 \end{align} \]

是正确的，其中 $ \lim_{x\to0}\frac{o(x^3)} {x^3}=0 $ 的原因是：函数族 $ \frac{o(x^3)} {x^3} $ 中所有的函数，在 $ x\to0 $ 时的极限都为0，那么原式也必然遵循这个规律，极限为0.

而这样的计算：

\[ \begin{align} \lim_{x\to0}\frac{x-\sin x} {x^3}&=\lim_{x\to0}\frac{x-(x+o(x^2))} {x^3}\\ &=\lim_{x\to0}\frac{o(x^2)}{x^3}\\ &=? \end{align} \]

无法计算下去的原因是：函数族 $ \frac{ o(x^2)} {x^3} $ 中的函数，在 $ x \to 0 $ 时的极限不相同，如 $ \frac {x^3} {x^3} $ 收敛到1，而 $ \frac{x^4} {x^3} $ 收敛到0. 整个计算过程错在：将 $ \sin x $ 展开成 $ x + o(x^2) $ 时精度太低，集合扩展得太大，将极限不同的其他函数也加入了这个集合中，导致最后极限不收敛。（但这个计算过程不收敛不能说明原式不收敛）

关于 $ \sin x $ 函数的泰勒展开（以及一些其他函数）的函数族韦恩图如图1所示：