1314：【例3.6】过河卒(Noip2002)
1314：【例3.6】过河卒(Noip2002)（递推法/动态规划法）
时间限制: 1000 ms 内存限制: 65536 KB
提交数: 18186 通过数: 7756
【题目描述】
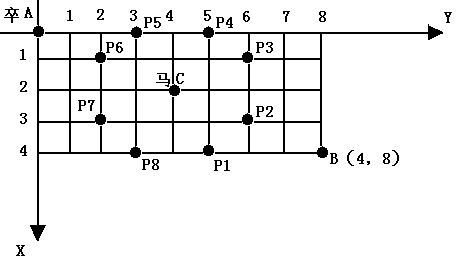
棋盘上A点有一个过河卒，需要走到目标B点。
卒行走的规则：可以向下、或者向右。同时在棋盘上的某一点有一个对方的马（如C点），该马所在的点和所有跳跃一步可达的点称为对方马的控制点，如图3-1中的C点和P1，……，P8，卒不能通过对方马的控制点。棋盘用坐标表示，A点(0,0)、B点(n, m) (n,m为不超过20的整数),同样马的位置坐标是需要给出的，C≠A且C≠B。现在要求你计算出卒从A点能够到达B点的路径的条数。
【输入】
给出n、m和C点的坐标。
【输出】
从A点能够到达B点的路径的条数。
【输入样例】
8 6 0 4
【输出样例】
1617
【题解】
思路：dfs会超时，卒只能向下或者向右走。可递推出路径数的总和:
f[i][j] = f[i-1][j] + f[i][j-1]。
最终的结果应该由 long long 保存。
【超时的DFS代码参考】
// https://www.freesion.com/article/52861256835/
#include<bits/stdc++.h>
using namespace std;
int a[21][21],vis[21][21],n,m,xx,yy,cnt=0;
int dir[8][2]={{-2,-1},{-1,-2},{2,-1},{1,-2},{2,1},{1,2},{-1,2},{-2,1}};
int dr[2][2]={{0,1},{1,0}};
bool check(int x,int y)
{
if(vis[x][y]==0&&x>=0&&x<=n&&y>=0&&y<=m)return true;
return false;
}
void dfs(int x,int y)
{
if(x==n&&y==m)
{
cnt++;
return;
}
for(int i=0;i<2;i++)
{
int nx=dr[i][0]+x;
int ny=dr[i][1]+y;
if(check(nx,ny))
{
vis[nx][ny]=1;
dfs(nx,ny);
vis[nx][ny]=0;
}
}
}
int main()
{
cin>>n>>m>>xx>>yy;
memset(vis,0,sizeof(vis));
for(int i=0;i<8;i++)
{
int nx=xx+dir[i][0];
int ny=yy+dir[i][1];
if(nx>=0&&nx<=n&&ny>=0&&ny<=m&&vis[nx][ny]==0)
vis[nx][ny]=1;
}
vis[xx][yy]=1;
vis[0][0]=1;
dfs(0,0);
cout<<cnt<<endl;
return 0;
}
【正确答案】
// https://www.freesion.com/article/52861256835/
#include<bits/stdc++.h>
using namespace std;
int vis[21][21],n,m,xx,yy;
int dir[8][2]={{-2,-1},{-1,-2},{2,-1},{1,-2},{2,1},{1,2},{-1,2},{-2,1}};
bool check(int x,int y)
{
if(vis[x][y]==0&&x>=0&&x<=n&&y>=0&&y<=m)return true;
return false;
}
long long f[21][21];
int main()
{
cin>>n>>m>>xx>>yy;
memset(vis,0,sizeof(vis));
for(int i=0;i<8;i++)
{
int nx=xx+dir[i][0];
int ny=yy+dir[i][1];
if(nx>=0&&nx<=n&&ny>=0&&ny<=m&&vis[nx][ny]==0)
vis[nx][ny]=1;
}
vis[xx][yy]=1;
vis[0][0]=1;
for(int i=1;i<=n;i++)
if(vis[i][0])break;
else f[i][0]=1;
for(int i=1;i<=m;i++)
if(vis[0][i])break;
else f[0][i]=1;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(check(i,j))
{
f[i][j]=f[i-1][j]+f[i][j-1];
}
}
}
cout<<f[n][m]<<endl;
return 0;
}
【我的答案】
# include <bits/stdc++.h>
using namespace std;
const int MAXLEN = 25;
long long int board[MAXLEN][MAXLEN];
const int direction[8][2] = {
{ 1, 2},
{-1, 2},
{ 1, -2},
{-1, -2},
{ 2, 1},
{-2, 1},
{ 2, -1},
{-2, -1}
};
int sizex, sizey;
int horsex, horsey;
# define CHECK(X,Y) ((X)>=0&&(X)<sizex&&(Y)>=0&&(Y)<sizey)
int main ()
{
cin >> sizex >> sizey >> horsex >> horsey;
sizex++;
sizey++;
board[horsex][horsey] = -1;
for(int i = 0; i < 8; i++){
if(CHECK(horsex+direction[i][0], horsex+direction[i][0])){
board[horsex+direction[i][0]][horsey+direction[i][1]] = -1;
}
}
for(int y = 0; y < sizey; y++){
if(board[0][y] == -1){
board[0][y] = 0;
break;// 很重要 ，从此往后都是0
}
else{
board[0][y] = 1;
}
}
for(int x = 0; x < sizex; x++){
if(board[x][0] == -1){
board[x][0] = 0;
break;// 很重要 ，从此往后都是0
}
else{
board[x][0] = 1;
}
}
for(int x = 1; x < sizex; x++){
for(int y = 1; y < sizey; y++){
if(board[x][y] == -1){
board[x][y] = 0;
}
else{
board[x][y] = board[x-1][y] + board[x][y-1];
}
}
}
printf("%lld\n", board[sizex-1][sizey-1]);
return 0;
}
// 2021年10月6日16:15:51
(完)
