嵊州D1T4 cf1174E 占梦人
嵊州D1T4 cf1174E
此题为改编题,原题:cf1174E
占梦人
占梦人一个晚上会做 n 个梦,编号为 1 ∼ n,她可以安排做这 n 个梦的顺序。
假如她第一个做了编号为 x 的梦,那么她的初始灵力值就是 x。
接着,如果她在灵力值为 x 的时候 做了编号为 y 的梦,他的灵力值会变成 gcd(x, y)。
只有当灵力值改变时,她才可能预言到一些事情。
她希望能预测到的事情尽量多,那么有多少种安排去做 n 个梦寻找的顺序呢?
请给出答案 %1000000007 的结果。
Input
一行一个整数 n。
Output
一行一个整数表示答案。
Examples
| dreams.in | dreams.out |
| 2 | 1 |
| 3 | 4 |
| 6 | 120 |
| 58462 | 250302017 |
Notes
对于所有数据,满足 2 ≤ n ≤ 107
Subtask1[28pts]
n ≤ 10
Subtask2[5pts]
n ≤ 13
Subtask3[20pts]
n ≤ 20
Subtask4[26pts]
n ≤ 106
Subtask5[21pts]
无特殊限制
Solve!
看到结尾的%1000000007
好熟悉呀!!!
好想翻书!
肯定做过!
好后悔!!!
所以,这告诉我们:
书到用时方恨少!
不瞎扯,继续讲吧!
首先,和上一题一样,先敲一个gcd(a,b)出来嘛。放那里总会有用的!
(光是这个gcd我就调试了10分钟呢。。。)
一定要背牢呀!
(说好不瞎扯的呢?)
咳咳。。。
继续!
int gcd(int x,int y) { return y==0?x:gcd(y,x%y);}
口诀:
若y仍然不为零,gcd(y,mod);
待到y等于零时,返回此时x!
接着!
原题题意
定义gi是排列p1,p2...pi的的GCD(长度为i的前缀GCD),f(p)是 g1,g2..gn中独特的元素个数
让fmax(n) 成为f(p)在所有整数1,2...n的排列中的最大值,给出整数n,给出满足f(p)=fmax(n)的排列个数 mod(1e9+7)
所以,首个元素s必然有最多的质因数。这样才能在之后n-1次gcd中,获得更多的变化嘛。
每次gcd改变时,只能从其中拿走一个质因数,这样我们可以保证有尽可能多的独特gcd。
解析题目
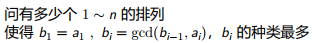
简单的,
因为n比较小
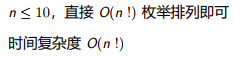
再看看
Subtask2[5pts]
n ≤ 13
我测试了一下,还用原方法会超时的。。。
打表吧?
枚举Subtask


即s只能被2和3整除,因为如果s有其他的质因数p(p>4),我们可以s/p*4,这样可以得到更多质因数。
s=2^x*3^y,即s只能被2和3整除,因为如果s有其他的质因数p(p>4),我们可以s/p*4,这样可以得到更多质因数。





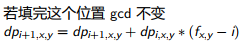
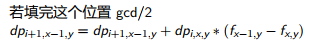
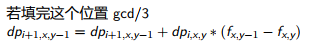


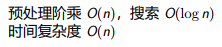
1 #include<cstdio> 2 #include<algorithm> 3 4 using namespace std; 5 6 int cal(int x, int y) {return y ? cal(y, x % y) + x / y : x > 1 ? 1e9 : -1;} 7 8 int n, i, ans; 9 10 int main() 11 { 12 //freopen("sleepingbeauty.in","r",stdin); 13 //freopen("sleepingbeauty.out","w",stdout); 14 15 ans = INT_MAX; 16 scanf("%d", &n); 17 for(int i = 1; i <= n; ++i) 18 ans = min(ans, cal(n, i)); 19 printf("%d", ans); 20 21 return 0; 22 }
记得消化!!!!!!!!!!!!!!!


