决策树
决策树(decision tree)是一种基本的分类与回归方法。在训练过程中,根据训练数据的属性来建立一棵决策树,从而实现快速地分类和回归。这篇文章将会讨论用于分类的决策树。
决策树的定义
决策树由结点(node)和有向边(directed edge)组成。结点可以分为两种类型:内部结点(inner node)和叶结点(leaf node)。内部结点表示一个特征或者属性,叶结点表示一个类。
下图展示了一个决策树:
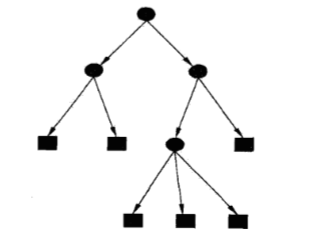
其中椭圆是内部结点,矩形是叶结点。
决策树的分类原理
决策树可以看做是一个if-then规则的集合,从根结点到叶结点的一条路径对应着一条规则 ,叶结点对应着规则的结论。
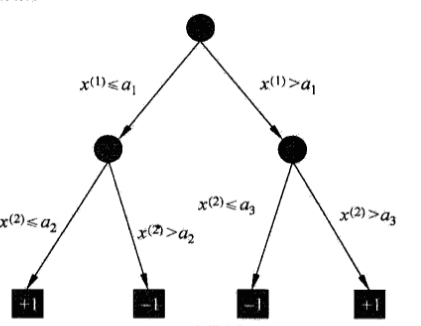
假设实例\(x\)有两个特征,也就是\(x=(x^{(1)},x^{(2)})\),我们可以根据上面的决策树来判断实例 \(x\) 是哪一类(对应+1和-1)。若 \(x^{(1)} \le a_1\) 并且 \(x^{(2)} > a_2\) 时,根据该决策树,实例 \(x\) 的输出为 -1。
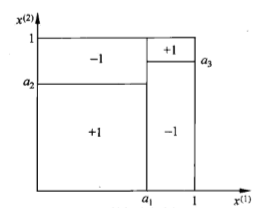
一棵决策树对应着特征空间上的一个划分,上面的决策树对应着下面的划分:
决策树的生成
首先将所有的实例都放在根结点,然后通过实例的某一属性的取值将训练数据分为若干个部分,每个部分对应一个子结点,对每个子结点递归地调用上面的操作,直至到达叶子结点,此时叶子结点中的所有实例都属于同一类。
一个例子
假如有以下的训练数据:
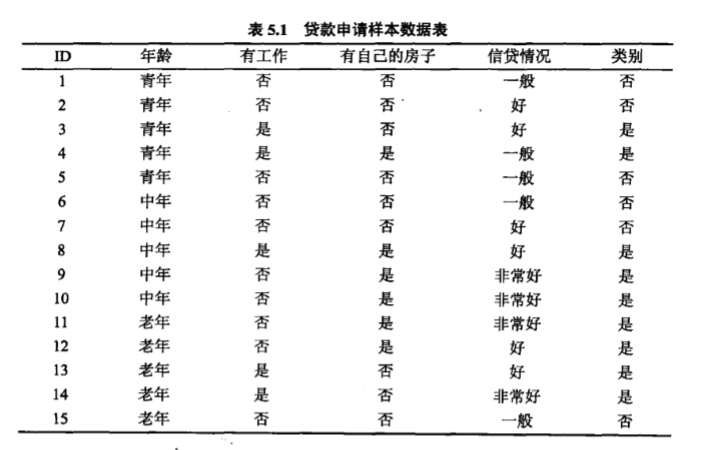
上表是一个贷款申请的训练数据,每一行代表一个申请人,申请人具有4个特征(属性),分别是年龄(3个取值:青年、中年、老年)、是否有工作(2个取值:是、否)、是否有自己的房子(2个取值:是、否)和信贷情况(3个取值:一般、好、非常好)。根据这15条训练数据来学习一个决策树,使用该决策树判断输入的申请人是否有贷款的资格。
首先这15个实例都在根结点,然后我们可以选择一个属性来对这15个人进行分类,申请人的4个属性都可以被用来分类,若使用年龄或者是否有工作来分类,则可以得到下面的决策树:

我们可以看到,当选择不同的属性来划分样本时,会得到不同形状的决策树,这些决策树有的泛化能力强,有的泛化能力弱。那么我们怎样选择划分属性使得我们能得到一个最好的决策树呢?信息增益(information gain)就是选择划分属性的标准。
信息增益
在介绍信息增益之前,需要了解熵(entropy)和条件熵(conditional entropy)的概念。
熵
在高中化学我们学过熵的概念,当时我们用熵来度量一个体系的混乱程度。熵越大,代表该体系越混乱,比如烟雾扩散就是一个熵增的过程。在信息论和概率统计中,熵则是随机变量不确定性的度量。熵越大,随机变量的不确定性也就越大。
设 \(X\) 是一个取有限个值的离散随机变量,其概率分布为:
则随机变量 \(X\) 的熵 \(H(X)\) 定义为:
当上式中的对数以2为底时,熵的单位为比特(bit);当上式中对数以自然对数 e 为底时,熵的单位为纳特(nat)。从上式我们可以看到,熵的取值只与随机变量 \(X\) 的分布有关,而与 \(X\) 的取值无关,所以也可以将随机变量 \(X\) 的熵 \(H(X)\) 记为 \(H(p)\),这样上式就写为:
假如随机变量 \(X\) 服从伯努利分布,也就是 \(X\) 只取两个值:0 和 1,取 0 的概率为 \(p\),取 1 的概率为 \(1-p(0≤p≤1)\) 。那么,随机变量 \(X\) 的熵 \(H(p)\) 为:
这时,熵 \(H(p)\) 随概率 \(p\) 的变化曲线如下(单位为比特):
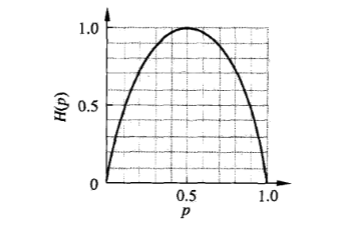
可以看到,当 \(p=0\) 或者 \(p=1\) 时,随机变量变成了必然事件,完全没有不确定性,所以熵 \(H(p)=0\) 为最小值。当 \(p=0.5\)时,熵 \(H(p)=1\) 取最大值,此时随机变量的不确定性也最大。
条件熵
条件熵对应条件概率。
设有随机变量 \((X,Y)\),其联合概率分布为:
则条件熵 \(H(Y|X)\) 表示在已知随机变量 \(X\) 的情况下,随机变量 \(Y\) 分布的不确定性。\(H(Y|X)\) 的定义为:
上式中,\(p_i\) 为边缘概率,也就是 \(p_i = P(X=x_i)=\Sigma_{j=1}^np_{ij}\) 。
经验熵和经验条件熵
当熵和条件熵计算所使用的概率是由数据估计(特别是极大似然估计)得到时,这时熵和条件熵分别被称为经验熵(empirical entropy)和经验条件熵(empirical conditional entropy)。
信息增益的定义
特征 \(A\) 对训练数据集 \(D\) 的信息增益 \(g(D,A)\) ,定义为集合 \(D\) 的经验熵 \(H(D)\) 与在特征 \(A\) 给定的条件下 \(D\) 的经验条件熵 \(H(D|A)\) 之差,也就是:
决策树依据信息增益来选择特征,信息增益大的特征具有更强的分类能力。
一个例子
继续考虑贷款申请人的训练数据 \(D\) :

我们首先根据是否有贷款能力来计算其经验熵 \(H(D)\),我们可以看到有贷款能力的有 9 个,没有贷款能力的有 6 个,则
我们分别使用 \(A_1,A_2,A_3,A_4\) 来代表年龄、有工作、有自己的房子以及信贷情况 4 个特征,分别计算它们的信息增益 \(g(D, A_i), i=1,2,3,4\),则
(1)当 \(A_1\) (年龄)作为分类特征时:
我们可以看到 \(A_1\) 有3个属性:青年、中年、老年。这3个属性将数据集 \(D\) 划分为了3个子集 \(D_1, D_2, D_3\),且\(|D_1|=|D_2|=|D_3|=5\),先考虑 \(D_1\),\(D_1\) 为年龄为青年的样本子集,它包含5条数据,其中可以贷款的占2条,不能贷款的占3条,所以
同理\(H(D_2) = -{2\over 5}log{2\over 5}-{3\over 5}log{3\over 5}\),\(H(D_3) = -{1\over 5}log{1\over 5}-{4\over 5}log{4\over 5}\)
所以条件熵
所以信息增益
同理可以求得\(g(D,A_2)=0.324\),\(g(D,A_3)=0.420\),\(g(D,A_4)=0.363\),可以看到\(g(D,A_3)=0.420\)最大,也就是使用 \(A_3\)(是否有自己的房子)划分数据集的信息增益最大,所以选择特征 \(A_3\) 对数据集进行划分。\(A_3\) 有两个取值,所以从根结点分裂出两个子结点,对子结点继续进行上面的操作,直到所有特征的信息增益均很小或者没有特征可以选择为止。
信息增益比
当使用特征的信息增益作为划分数据集的准则时,存在偏向于选择取值较多的特征的问题。而信息增益比(information gain ratio)可以避免这一问题,这是特征选择的另一准则。信息增益比的定义如下:
特征 \(A\) 对数据集 \(D\) 的信息增益比 \(g_R(D, A)\) 定义为其信息增益 \(g(D, A)\) 与训练数据集 \(D\) 关于特征 \(A\) 的值的熵 \(H_D(A)\) 之比,也就是:
其中,$H_D(A) = -\Sigma_{i=1}^n \frac{|D_i|}{|D|} log_2 \frac{|D_i|}{|D|} $ 。
决策树的生成算法
生成一棵决策树的经典算法有ID3、C4.5和CART。ID3 中的 ID 是是 Iterative Dichotomiser (迭代二分器)的简称,C4.5 中的 C 是 Classifier(分类器)的简称,CART 是 Classification and Regression Tree(分类和回归树)的简称。ID3 和 C4.5 生成的决策树用来分类,而 CART 生成的决策树即可以用来分类,也可以用来回归。
ID3 、C4.5 和 CART(用于分类)的算法步骤如下所示:

其中 3 种算法的不同在于第 8 步,ID3 选择信息增益最大的属性作为划分属性, C4.5 选择信息增益比最大的属性作为划分属性。CART 则选择基尼指数(Gini index)作为特征选择的标准。
基尼指数
在分类问题中,假设有 \(K\) 个类,样本点属于第 \(k\) 类的概率为 \(p_k\),则概率分布的基尼指数定义为:
对于给定的样本集合 \(D\),其基尼指数为:
其中,\(C_k\) 是 \(D\) 中属于第 \(k\) 类的样本子集,\(K\)是类的个数。
假设特征 \(A\) 具有 \(v\) 个属性值 \(\{a^{(1)}, a^{(2)},...,a^{(v)}\}\),特征 \(A\) 的取值等于 \(a^{(v)}\) 的集合记为 \(D^v\),则属性 \(A\) 的基尼指数定义为:
基尼指数 \(Gini(D)\) 表示集合 \(D\) 的不确定性,基尼指数 \(Gini(D,A)\) 表示经 \(A=a\) 分割后集合 \(D\) 的不确定性。基尼指数越大,集合的不确定性也就越大,所以我们选择基尼指数小的属性进行划分。
决策树的剪枝
决策树生成算法递归地生成决策树,直到不能进行下去为止。有时,在算法结束后,可能会返回一棵分支非常多的决策树,这棵决策树对训练数据具有很好的分类效果,然而在新的测试数据的表现则没有那么准确,从而产生了过拟合现象。为了避免过拟合,我们可以对决策树进行剪枝,使其不那么复杂,从而获得更好的泛化能力。具体地,剪枝就是从决策树上剪掉一些子树或者叶结点,并将其根结点或者父结点作为新的叶结点的过程。剪枝可以分为预剪枝(prepruning)和后剪枝(postpruning)。预剪枝发生在决策树生成过程中,在对结点进行划分之前,先考虑当前的划分是否能带来泛化性能的提升,若能提升,则划分,否则将当前结点置为叶结点。后剪枝发生在决策树生成之后,这时自底向上地对该决策树的非叶结点进行考察,若将结点对应的子树替换为叶结点能带来泛化性能的提升,则将该子树替换为叶结点。
怎么判断剪枝前后一棵决策树的泛化性能是否有所提升呢?我们可以将训练数据的一部分留出作为验证集,我们在验证集上评判剪枝前后决策树的分类精度,若剪枝后的精度高于剪枝前,则泛化性能提升,应该剪枝,否则不剪枝。
预剪枝
继续考虑前面的贷款数据:

我们将编号为 1~10 的 10 个样本作为训练集,编号为 11~15 的 5 个样本作为验证集。起初所有的实例都在根结点,如下:

我们将10个实例中占多数的类当做该结点的类,可以看到10个样本中有5个有贷款资格,5个没有。我们随便选择一个:没有贷款资格。此时,我们用验证集来测试该决策树,发现只有编号第 15 的样例被分类成功,精度为 1/5*100% = 20% 。通过前面我们知道特征“是否有自己的房子”的信息增益最大,所以我们使用该特征将根结点分为 2 个结点,如下:

“是否有自己的房子”将编号 1~10 的数据分为两类:编号(4,8,9,10)和编号(1,2,3,5,6,7),在(4,8,9,10)中有贷款资格的占多数,所以该结点的类别为有贷款资格,同理(1,2,3,5,7)所在结点的类别为没有贷款资格。我们用验证集测试发现编号为 11,12,15 的实例被正确分类,精度 3/5*100%=60% > 20%,泛化性能提升,所以无需剪枝。
后剪枝
后剪枝自底向上将非叶结点变为叶结点后通过分类精度来评价泛化性能,若精度提高,则将该非叶节点变为叶结点(剪枝),否则不做改动。
决策树的实现
这里不再造轮子了,直接使用python库scikit-learn来生成一棵决策树来解决上面的贷款分类问题。 使用scikit-learn还可以以图形的方式把生成的决策树显示出来,用过的都说好。
首先对贷款数据进行一下处理,也就是对中文属性值进行编码,我们使用1、2、3分别代表年龄中的青年、中年和老年,使用0、1分别代表没有工作和有工作,使用0、1分别代表没有房子和有房子,使用1、2、3分别代表信贷情况一般、好、非常好,使用0、1分别代表有贷款资格和没有贷款资格。处理后的数据如下:
1,0,0,1,0
1,0,0,2,0
1,1,0,2,1
1,1,1,1,1
1,0,0,1,0
2,0,0,1,0
2,1,1,2,0
2,1,1,2,1
2,0,1,3,1
2,0,1,3,1
3,0,1,3,1
3,0,1,2,1
3,1,0,2,1
3,1,0,3,1
3,0,0,1,0
将这些数据保存到data.txt,并使用pandas读取:
from sklearn import tree
import pandas as pd
import numpy as np
import graphviz
df = pd.read_csv("D:\\data.txt", header=None)
# 属性值
xdata = df.loc[:,:3]
#类别
ydata = df.loc[:,4]
然后使用scikit-learn中的DecisionTreeClassifier来构建一棵决策树,DecisionTreeClassifier的用法以及参数含义可以参考文档。
# 使用信息增益作为划分标准
clf = tree.DecisionTreeClassifier(criterion='entropy')
clf = clf.fit(xdata, ydata)
这样就得到了一棵决策树clf,下面我们就可以使用clf来对新的实例进行预测:
# 青年人、没工作、有房子、信用好
clf.predict(np.array([1,0,1,1]).reshape(1,-1))
结果:
array([1], dtype=int64)
1代表有贷款资格。再试一个:
# 青年人、有工作、没房子、信用好
clf.predict(np.array([1,1,0,1]).reshape(1,-1))
结果:
array([0], dtype=int64)
0代表没有贷款资格。
接着我们使用库graphviz 来画出决策树(如果没有安装并且使用conda管理包,则使用命令conda install python-graphviz安装即可) 。
dot_data = tree.export_graphviz(clf, out_file=None)
graph = graphviz.Source(dot_data)
dot_data = tree.export_graphviz(clf, out_file=None,
feature_names=['age','work','house','credit'],
class_names=['no','yes'], # 这个参数以类别升序排列,这个例子中类别是0,1,代表没有/有资格
filled=True, rounded=True,
special_characters=True)
graph = graphviz.Source(dot_data)
graph
结果:
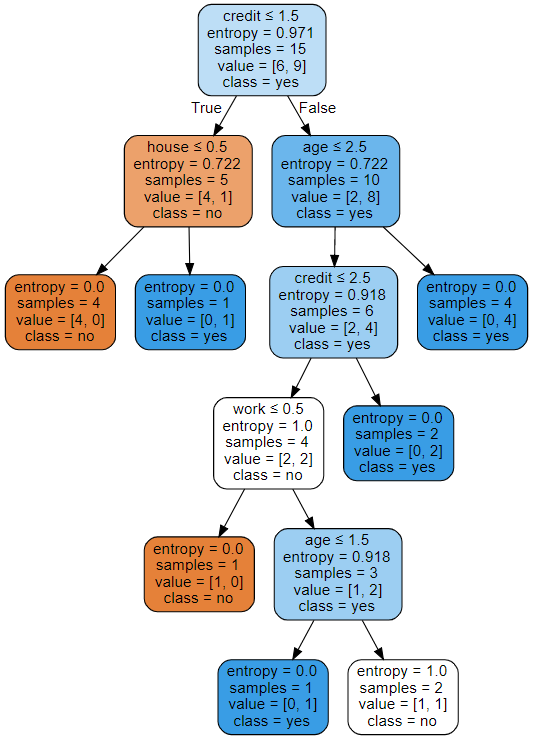
上面用到了export_graphviz函数,其使用方法、参数含义见文档。可以看到scikit-learn中的决策树算法并没有使用前面计算的信息增益最大的划分属性“是否有房子”做第一个划分,原因我认为有两个:1、这个算法把离散值当做连续值处理了;2、scikit-learn 使用 CART 算法的优化版本,与前面讲的算法并不完全相同。
完整代码如下:
from sklearn import tree
import pandas as pd
import numpy as np
import graphviz
df = pd.read_csv("D:\\data.txt", header=None)
# 属性值
xdata = df.loc[:,:3]
#类别
ydata = df.loc[:,4]
# 使用信息增益作为划分标准
clf = tree.DecisionTreeClassifier(criterion='entropy')
clf = clf.fit(xdata, ydata)
# 青年人、有工作、没房子、信用好
clf.predict(np.array([1,1,0,1]).reshape(1,-1))
dot_data = tree.export_graphviz(clf, out_file=None)
graph = graphviz.Source(dot_data)
dot_data = tree.export_graphviz(clf, out_file=None,
feature_names=['age','work','house','credit'],
class_names=['no','yes'], # 这个参数以类别升序排列,这个例子中类别是0,1,代表没有/有资格
filled=True, rounded=True,
special_characters=True)
graph = graphviz.Source(dot_data)
graph
总结
决策树是一种常用的分类和回归模型。决策树的生成算法一般包括3个部分:特征选择、树的生成和树的剪枝。特征选择常使用信息增益、信息增益比和基尼指数作为选择标准,通常选择信息增益最大、信息增益比最大、基尼指数最小的特征。常用的决策树生成算法有ID3、C4.5以及CART。决策树的剪枝可以防止过拟合,根据剪枝的时间不同,剪枝可以分为预剪枝和后剪枝。
参考
1、李航《统计学习方法》
2、周志华《机器学习》



 浙公网安备 33010602011771号
浙公网安备 33010602011771号