模拟退火算法

一、什么是模拟退火算法

1、爬山算法

在了解模拟退火算法之前，先来看一下爬山算法：爬山算法是一种贪心算法，该算法每次从当前的解空间中选取一个解作为最优解，直到达到一个局部最优解。假设函数f(x)的图像如下图：

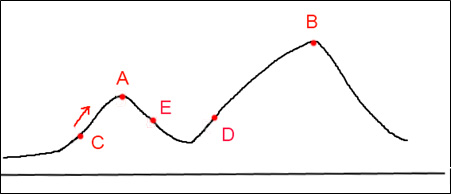
现在使用爬山算法来求f(x)的最大值，若C为当前最优解，则爬山算法搜索到A就会停止搜索，这会获得一个局部最优解，而不是全局最优解。

2、模拟退火算法

继续考虑寻找f(x)最大值的问题，爬山算法搜索到A点时就会停止搜索，原因是A点左右的值均小于A点的值。模拟退火算法采用的解决办法是以一定的概率选择A两边的点，尽管A两边的点并不是局部最优解，这样就有一定的概率搜索到D点，从而搜索到B点，最终获得了全局最优解。
上文中的一定概率来自于固体退火原理：当固体温度较高时，物质内能较大，固体内部分子运动剧烈；当温度逐渐降低时，物体内能也随之降低，分子运动趋于平稳；当固体温度降到常温时，固体内部分子运动最终平稳。根据Metropolis准则，粒子在温度T时趋于平衡的概率为e^(-ΔE/(kT))，其中E为温度T时的内能，ΔE为其改变量，k为Boltzmann常数。

二、模拟退火算法步骤

三、模拟退火算法流程图

四、模拟退火算法伪代码

/*
* J(y)：在状态y时的评价函数值
* Y(i)：表示当前状态
* Y(i+1)：表示新的状态
* r： 用于控制降温的快慢
* T： 系统的温度，系统初始应该要处于一个高温的状态
* T_min ：温度的下限，若温度T达到T_min，则停止搜索
*/
while( T > T_min )
{
　　dE = J( Y(i+1) ) - J( Y(i) ) ; 

　　if ( dE >=0 ) //表达移动后得到更优解，则总是接受移动
       Y(i+1) = Y(i) ; //接受从Y(i)到Y(i+1)的移动
　　else
　　{
       // 函数exp( dE/T )的取值范围是(0,1) ，dE/T越大，则exp( dE/T )也
      if ( exp( -dE/T ) > random( 0 , 1 ) )
      Y(i+1) = Y(i) ; //接受从Y(i)到Y(i+1)的移动
　　}
　　T = r * T ; //降温退火 ，0<r<1 。r越大，降温越慢；r越小，降温越快
　　/*
　　* 若r过大，则搜索到全局最优解的可能会较高，但搜索的过程也就较长。若r过小，则搜索的过程会很快，但最终可能会达到一个局部最优值
　　*/
　　i ++ ;
}

五、使用模拟退火算法解决旅行商问题

旅行商问题(TravelingSalesmanProblem，TSP)是一个经典的组合优化问题。经典的TSP可以描述为：一个商品推销员要去若干个城市推销商品，该推销员从一个城市出发，需要经过所有城市后，回到出发地。应如何选择行进路线，以使总的行程最短。
该问题可以使用模拟退火算法解决，python代码如下：

import math
import time
import random

# 初始温度
T = 50000
# 最低温度
T_end = 1e-8
# 在每个温度下的迭代次数
L = 100
# 退火系数
delta = 0.98

# 31个城市的坐标
citys = [[1304,2312],[3639,1315],[4177,2244],[3712,1399],[3488,1535],[3326,1556],[3238,1229],[4196,1004],[4312,790],[4386,570],[3007,1970],[2562,1756],[2788,1491],[2381,1676],[1332,695],[3715,1678],[3918,2179],[4061,2370],[3780,2212],[3676,2578],[4029,2838],[4263,2931],[3429,1908],[3507,2367],[3394,2643],[3439,3201],[2935,3240],[3140,3550],[2545,2357],[2778,2826],[2370,2975]]
# 存储两个城市之间的距离
d = [[0 for i in range(31)] for j in range(31)]
# 存储一条路径
ans = []

# 计算降温次数
cnt=0

# 计算两个城市之间的距离
def get_city_distance():
    for i in range(len(citys)):
        for j in range(i, len(citys)):
            d[i][j] = d[j][i] = math.sqrt((citys[i][0]-citys[j][0])**2 + (citys[i][1]-citys[j][1])**2)

# 使用随机交换路径中两个城市的位置来产生一条新路径
def create_new(a):
    i = random.randint(0, len(a)-1)
    j = random.randint(0, len(a)-1)
    a[i], a[j] = a[j], a[i]
    return a

# 获取路径的长度
def get_route_distance(a):
    dist = 0
    for i in range(len(a)-1):
        dist+=d[a[i]][a[i+1]]
    return dist
    
def saa():
    get_city_distance()
    cnt = 0
    ans = range(0, len(citys))
    t = T
    result = 0
    while t >= T_end:
        for i in range(0, L):
            ans_new = create_new(ans)
            d1, d2 = get_route_distance(ans), get_route_distance(ans_new)
            de = d2 - d1
            result = d1
            if de<0:
                ans = ans_new
                result = d2
            else:
                if(math.e**(-de/T) > random.random()):
                    ans = ans_new
                    result = d2
        t = t * delta
        cnt+=1
    print "路径如下："
    print ans
    print "路径长度："
    print result
    print "降温次数："
    print cnt
    
start = time.time()
saa()
end = time.time()
print "运行耗时：" + str(end-start) + "s"

输出：

路径如下：
[5, 18, 29, 28, 6, 24, 12, 17, 15, 27, 21, 1, 22, 9, 8, 23, 19, 25, 30, 16, 26, 13, 14, 7, 11, 20, 4, 2, 3, 0, 10]
路径长度：
40605.6088359
降温次数：
1448
运行耗时：2.93400001526s

六、参考

1、http://www.cnblogs.com/heaad/archive/2010/12/20/1911614.html
2、https://www.cnblogs.com/lyrichu/p/6688459.html