最小生成树

一、定义

1、生成树

在一个无向连通图中，如果存在一个连通子图包含原图中的所有结点和部分边，且这个子图不存在回路，那么该子图被称为原图的一棵生成树。

2、最小生成树

所有生成树中，边权和最小的那一棵（或那几棵）叫做最小生成树（MST）。

 

二、构造算法

有两种算法来构造最小生成树：普里姆（Prim）算法和克鲁斯卡尔（Kruskal）算法。

三、普里姆（Prim）算法

算法步骤：

1、在图G=(V, E)（V表示顶点，E表示边）中，从集合V中任取一个顶点（起始点）放入集合 U中，这时 U={v0}，集合T(E)为空。

2、从v0出发寻找与U中顶点相邻（另一顶点在V中）权值最小的边的另一顶点v1，并使v1加入U。即U={v0,v1 }，同时将该边加入集合T(E)中。

3、重复2，直到U=V为止。

这时T(E)中有n-1条边，T = (U, T(E))就是一棵最小生成树。

构造过程：

 

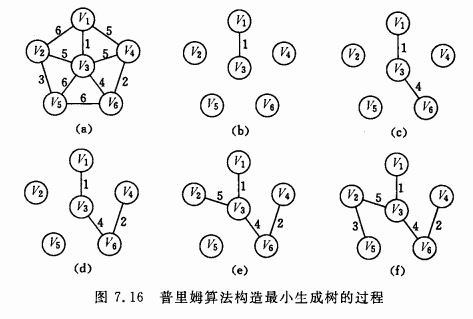
算法模板（hdoj1233）：

/**
 * 假设图中有n个结点，m条边（代码中m=n*(n-1)/2），使用邻接矩阵map[][]存储图，
 * 求图中最小生成树的边权值。具体输入输出要求参见hdoj1233。
 */
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;

const int INF = 0x7fffffff;
const int N = 100 + 10;
int map[N][N];
int dist[N];   
int n;

void prim()
{
    int min_edge, min_node;
    for (int i = 1;i <= n;i++)
        dist[i] = INF;
    int ans = 0;
    int now = 1;
    for (int i = 1;i < n;i++)
    {
        dist[now] = -1;
        min_edge = INF;
        for (int j = 1;j <= n;j++)
        {
            if (j != now && dist[j] >= 0)
            {
                if (map[now][j]>0)
                    dist[j] = min(dist[j], map[now][j]);
                if (dist[j] < min_edge)
                {
                    min_edge = dist[j];    //min_edge存储与当前结点相连的最短的边
                    min_node = j;
                }
            }
        }
        ans += min_edge;    //ans存储最小生成树的长度
        now = min_node;
    }
    printf("%d\n", ans);
}

int main()
{
    while (scanf("%d", &n) == 1 && n)
    {
        memset(map, 0, sizeof(map));
        int a, b, c;
        int nums = n*(n - 1) / 2;
        for (int i = 0; i < nums; i++)
        {
            scanf("%d%d%d", &a, &b, &c);
            map[a][b] = c;
            map[b][a] = c;
        }
        prim();
    }
    return 0;
}

prim算法涉及到两个集合V和U，V包含了图中所有结点，U则包含了当前最小生成树中的结点。上面代码中的数组dist[]存储了从集合U中的结点到集合V-U的结点的最短距离，如果编号为i的结点已经在U中了，则令dist[i]=-1。每次从V-U中选取结点添加到U时，则选取最小dist[]值对应的那个结点，dist[]在循环过程中是不断更新的。

三、克鲁斯卡尔（Kruskal）算法

 算法步骤：

1、初始时所有结点属于孤立的集合；

2、按照边权递增顺序遍历所有的边，若遍历到边的两个定点属于不同的集合（该边即为连通这两个集合的边中权值最小的那条），则确定该边为最小生成树上的一条边，并将这条边的两个顶点所属的集合合并；

3、遍历完所有边后，若原图上所有结点属于同一个集合，则原图结点和被选中的边构成最小生成树；否则原图不连通，最小生成树不存在。

构造过程：

 

算法模板（hdoj1233）：

/**
 * 假设图中有n个结点，m(代码中m=n*(n-1)/2)条边，使用邻接矩阵map[][]存储图，
 * 求图中最小生成树的边权值。具体输入输出要求参见hdoj1233。
 */
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
using namespace std;

struct Edge
{
    int a, b, dist;

    Edge() {}
    Edge(int a, int b, int d) :a(a), b(b), dist(d) {}
    bool operator < (Edge edge)    //按边长从短到长排序
    {
        return dist < edge.dist;
    }
};

const int N = 100 + 10;
int p[N];    //并查集使用
vector<Edge> v;
int n;

int find_root(int x)
{
    if (p[x] == -1)
        return x;
    else return find_root(p[x]);
}

void kruskal()
{
    memset(p, -1, sizeof(p));
    sort(v.begin(), v.end());
    int ans = 0;
    for (int i = 0; i < v.size(); i++)
    {
        int ra = find_root(v[i].a);
        int rb = find_root(v[i].b);
        if (ra != rb)
        {
            ans += v[i].dist;
            p[ra] = rb;
        }
    }
    printf("%d\n", ans);
}

int main()
{
    while (scanf("%d", &n) == 1 && n)
    {
        int a, b, d;
        int nums = n*(n - 1) / 2;
        v.clear();
        for (int i = 0; i < nums; i++)
        {
            scanf("%d%d%d", &a, &b, &d);
            v.push_back(Edge(a, b, d));
        }
        kruskal();
    }
}