数据结构与算法记录——函数递归
问题说明
售票工作正在进行，每张票为50元，现在有m+n人排队等待购票，其中有m人手持面额为50元，n人手持面额为100元，假设售票处开始没有零钱可找，那么若想使售票处不会出现找不开零钱的局面，假设拿同样面值的人对换位置为同一种方案。
问题梳理
1、开局没有零钱需要解决（第一人必须是持有面额为50元的人）
2、排队只讨论手持面额情况
解决过程
问题抽象
需要解决的问题相当于对两种不同的东西进行排队（50和100这两种东西），要求就是队列中每一项前面的50必须大于等于100这样才能满足问题一。
问题解决
排队抽象化其实相当于对小模块进行扩充，在此题中，只有前面的m+n-1项中满足m>=n即可。比如：只有队列1—3满足要求才能继续扩充第四个（回溯过程判断），否则这种排法就不满足要求。
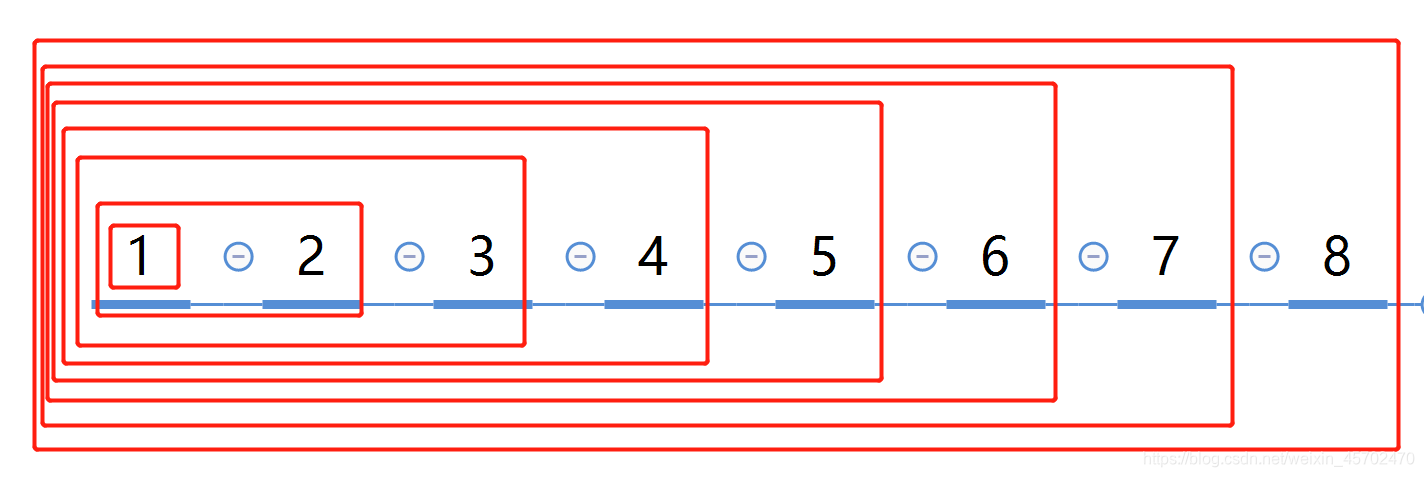
根据情况可以得知几种边界值情况（m为50面额数，n为100面额数）
1、全为50的面额(n=0)：则只有一种排法。
2、50的小于100(m<n)：无法排列，因为总有100的面额无法解决。
3、50的大于100(m>n)：可以进一步排。
int f(int m,int n){
if(n==0) return 1;
else if(m<n) return 0;
else return f(m-1,n)+f(m,n-1);
函数递归思路
函数递归过程中有递归和回溯两个过程。
此题中递归相当于把所有的排队方法都罗列一遍，而递归过程相当于把这些排列进行过滤，满足要求的进行标记累加，不满足的直接pass掉。回溯过程相当于上图中的扩充，只有较短部分满足要求才能继续扩充，即把大问题分为小部分解决，在小部分解决的基础上判断更大部分。
函数递归过程（罗列所有可能）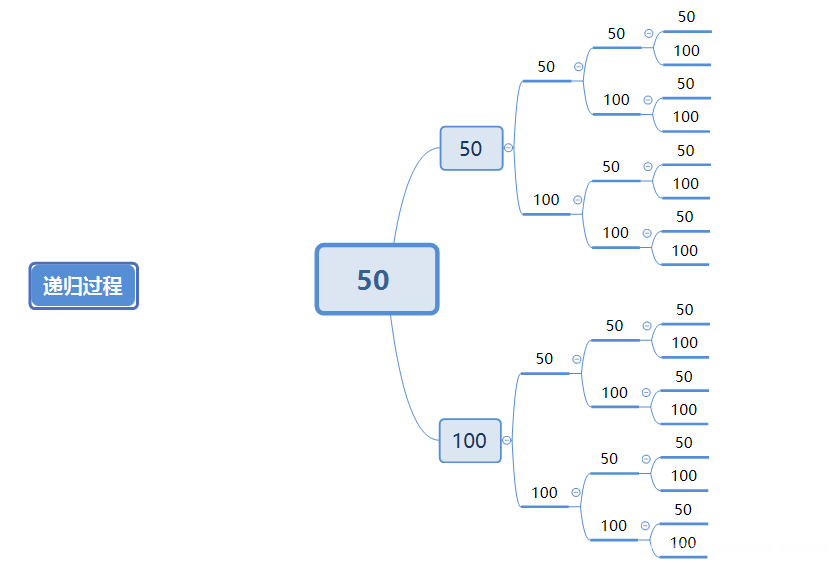
函数回溯过程即判断每一条路符不符合规则，若符合则记1。
完整代码
#include<stdio.h>
int f(int m,int n) {
if(n==0) return 1;
else if(m<n) return 0;
else return f(m-1,n)+f(m,n-1);
}
void main() {
int m,n;
scanf("%d%d",&m,&n);
printf(" %d",f(m,n));
}
测试结果
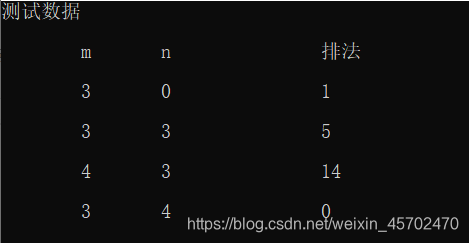
总结
- 函数递归最终会归到一个具体的值即边界值。所以可以根据边界值来进一步找寻整个过程的规律。
- 在排队等类似的递归中递归过程可以罗列出所有的情况，而回溯过程可以对所有过程进行进一步的判断。
- 缺点：有大量重复计算，数值较大时占用空间较多。
