汉罗塔问题

 

懒汉式递归——瞬间明白汉诺塔问题

Q. 为什么会有递归？

A. 因为我们是人，不是电脑！我们的working
memory有限！

游戏规则：

有A,B,C三根针，将A针上N个从小到大叠放的盘子移动到C针，一次只能移动一个，不重复移动，小盘子必须在大盘子上面。

 

问题：

总的移动次数是多少？

 

分析：

首先明确，我们的目标是将A针上所有N个盘子移动至C针。而对于B针，我们可以将之看成一个中转站。

这个问题，顺向思维或者逆向思维道理是相同的，都太麻烦。我们不妨从中间开始思考。

||： 规则要求小盘子必须在大盘子之上。试想这个过程中，必然会经历那么一个步骤，即有一大坨N-1个盘子在B针这个中转站，而我们正将最大那个盘子（即第N个盘子）从A针移动至C针。

 

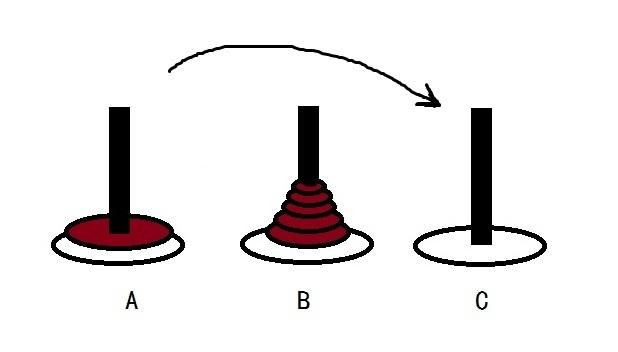
【图例】

 

只有经历“移动最大盘子”这个步骤，余下的事情才有可能实现。而在此之前，我们所要做的事情，就是让“移动最大盘子”这个步骤得以实现。

现在，游戏整个过程以“移动最大盘子”为中央，被分为了两部分。即（前）“将那坨N-1个盘子从A针移动到B针”，(中)“移动最大盘子”，(后)“将坨N-1个盘子从B针移动到C针”。

这是我们意识到，（前）与（后）操作道理是相似的。不去管那个最大盘子，（前）是以C针为中转站，（后）是以A针为中转站。因此两者所需的移动次数应当是相等的。这意味着我们只要计算出其中一者的移动次数，然而乘以2，在加上“移动最大盘子”的那1次，就是这场游戏的总移动次数了。

用数学语言表达，假设（前）“将N-1个盘子从A针移动到B针”所需次数为Hn-1，总移动次数为Hn，那么可以得出的关系就是：Hn=Hn-1
x 2 + 1.

其实当我们得出这个算式的时候，稍微聪明一点的人已经明白，这就是一个递推公式，可以直接用此公式得出Hn的通解。

但是LZ比较笨，就是不明白，为什么这个公式就可以套用呢？

那么就干脆继续思考吧。

让我们再想象一个情景：最大那个盘子在刚刚从A针被移动到C针，而那坨N-1个盘子还在B针蠢蠢欲动地等待着，即处于（中）->(后)的这个状态。

怎么移动这N-1个盘子呢？

其实这时候，问题已经回到了笔者标示“||：”符号的地方。“||：”是乐谱中的反复记号，而我们要做的，就是重复上面的步骤，但是要将N替换为N-1，因为现在只剩下N-1个盘子需要移动。而中转站则从B变成了A（鉴于这时盘子都在B针）。目标仍然是C针。下一次重复的时候，只剩下N-2个盘子需要移动，中转站又回到B，目标不变仍然是C针。……整个过程中，变化的只是中转站（在A与B之间轮换），以及剩下那些所需要移动的盘子的总数（越来越少）而已。

那么那个大盘子怎么办？不去管它吗？？

正解！！

因为你已经把它移到C针，已经完成了这个移动步骤，它不会影响之后的操作。提醒自己牢记游戏规则，大盘子永远在小盘子下面，而你也不需要再重复移动它——“不重复移动”，正是游戏规则的要求！

于是
Hn=Hn-1 x 2 + 1 这个公式，就可以套用、套用、套用……直到H3=7，H2=3，H1=1。

最后，用最懒的数学归纳法证明通项公式
Hn = 2^n - 1 吧！没办法，LZ就是比较懒嘛~

不管这个传说的可信度有多大，如果考虑一下把64片金片，由一根针上移到另一根针上，并且始终保持上小下大的顺序。这需要多少次移动呢?这里需要递归的方法。假设有n片，移动次数是f(n).显然f(1)=1,f(2)=3,f(3)=7，且f(k+1)=2*f(k)+1。此后不难证明f(n)=2^n-1。n=64时，

假如每秒钟一次，共需多长时间呢？一个平年365天有31536000 秒，闰年366天有31622400秒，平均每年31556952秒，计算一下：

18446744073709551615秒

这表明移完这些金片需要5845.54亿年以上，而地球存在至今不过45亿年，太阳系的预期寿命据说也就是数百亿年。真的过了5845.54亿年，不说太阳系和银河系，至少地球上的一切生命，连同梵塔、庙宇等，都早已经灰飞烟灭。

 

宇宙寿命

如果移动一个圆盘需要1秒钟的话，等到64个圆盘全部重新落在一起，宇宙被毁灭是什么时候呢？

让我们来考虑一下64个圆盘重新摞好需要移动多少次吧。1个的时候当然是1次，2个的时候是3次，3个的时候就用了7次......这实在是太累了

因此让我们逻辑性的思考一下吧。

3个的时候能够移动最大的3盘时如图所示。

到此为止用了7次。

接下来如右图，在上面再放上3个圆盘时还要用7次（把3个圆盘重新放在一起需要的次数）。[4] 

因此，4个的时候是

“3个圆盘重新摞在一起的次数”+1次+“3个圆盘重新摞在一起需要的次数”

=2x“3个圆盘重新摞在一起的次数”+1次

=15次。

那么，n个的时候是

2x“（n-1）个圆盘重新摞在一起的次数”+1次。

由于1 个的时候是1次，结果n个的时候为（2的n次方减1）次。

1个圆盘的时候 2的1次方减1

2个圆盘的时候 2的2次方减1

3个圆盘的时候 2的3次方减1

4个圆盘的时候 2的4次方减1

5个圆盘的时候 2的5次方减1

........

n个圆盘的时候 2的n次方减1

也就是说，n=64的时候是（2的64次方减1）次。

因此，如果移动一个圆盘需要1秒的话，

宇宙的寿命=2的64次方减1（秒）

2的64次方减1到底有多大呢？动动计算器，答案是一个二十位的数字约是

1.84467440*10^19

用一年=60秒x60分x24小时x365天来算的话，大约有5800亿年吧。

太阳及其行星形成于50亿年前，其寿命约为100亿年。

汉诺塔问题在数学界有很高的研究价值，而且至今还在被一些数学家们所研究。

也是我们所喜欢玩的一种益智游戏，它可以帮助开发智力，激发我们的思维。

印度传说

和汉诺塔故事相似的，还有另外一个印度传说：舍罕王打算奖赏国际象棋的发明人──宰相西萨·班·达依尔。国王问他想要什么，他对国王说：“陛下，请您在这张棋盘的第1个小格里赏给我一粒麦子，在第2个小格里给2粒，第3个小格给4粒，以后每一小格都比前一小格加一倍。请您把这样摆满棋盘上所有64格的麦粒，都赏给您的仆人吧！”国王觉得这个要求太容易满足了，就命令给他这些麦粒。当人们把一袋一袋的麦子搬来开始计数时，国王才发现：就是把全印度甚至全世界的麦粒全拿来，也满足不了那位宰相的要求。

那么，宰相要求得到的麦粒到底有多少呢？总数为

1+2+2^2 + … +2^63=2^64-1

等于移完汉诺塔所需的步骤数。我们已经知道这个数字有多么大了。人们估计，全世界两千年也难以生产这么多麦子！

'''
source  原来的盘子
targer  移到目标柱子的盘子
helper  中间柱子的盘子
'''
def hanoi22(n,source,target,helper):
     pass
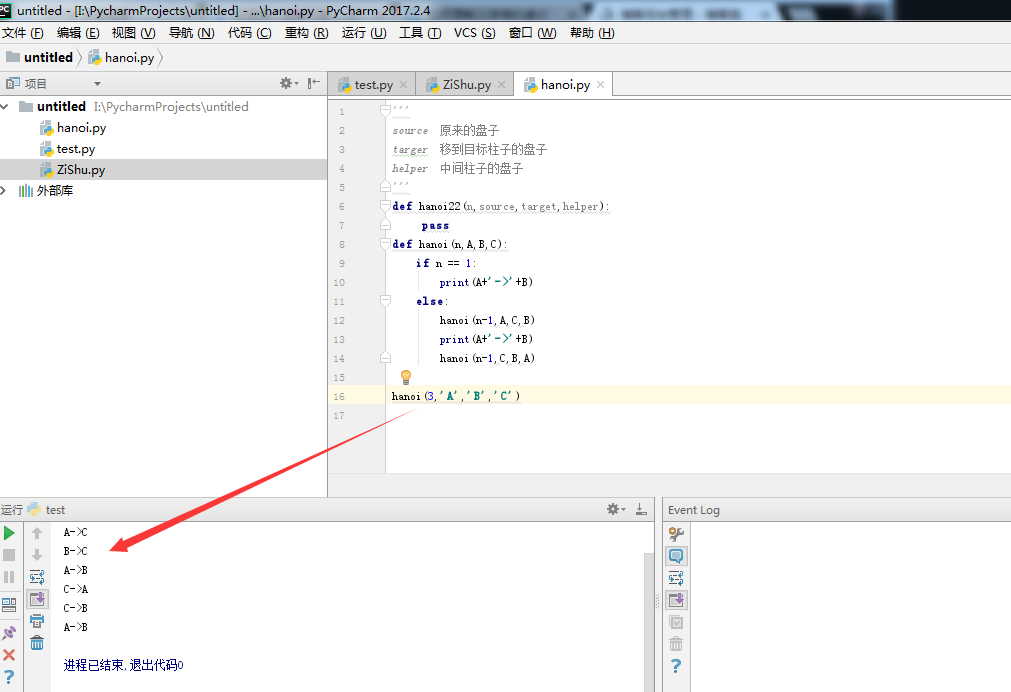
def hanoi(n,A,B,C):
    if n == 1:
        print(A+'->'+B)
    else:
        hanoi(n-1,A,C,B)
        print(A+'->'+B)
        hanoi(n-1,C,B,A)

hanoi(3,'A','B','C')