二叉搜索树的实现
最近复习了二叉搜索树的基础知识,总结下,然后用C++实现二叉搜索树的插入,删除,查找等,也是为了实现红黑树做铺垫。
一个二叉搜索树结构如下,父节点做子树都比父节点小,右子树都比父节点大。
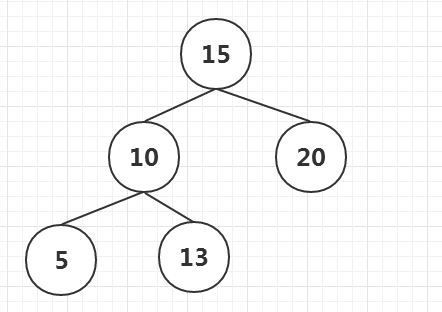
插入节点12后,如下
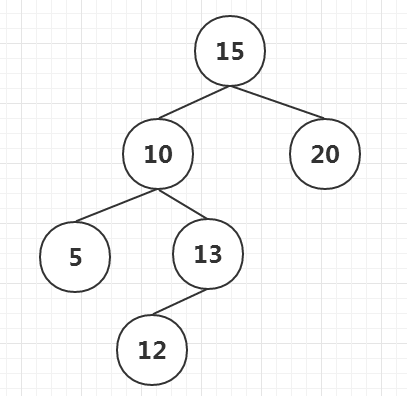
删除的情况,删除节点A,判断节点A是否为叶子节点,如果是叶子结点直接删除即可。如果叶子A有且仅有一个子节点B,那么用B替代节点A。
如果节点A有两个子节点,找到前驱节点B,用前驱节点B(或者后继节点)替代节点A。有一种特殊的情况,就是前驱节点有左孩子,或者后继节点有右孩子,
这种情况需要仔细考虑。仅拿前驱节点举例子,前驱节点的父节点为C,前驱节点的左孩子为D,那么将D的父节点间设置为C,C的子节点设置为D。如果前驱节点B有右孩子怎么办?B是不可能有右孩子的,否则他的右孩子就是节点A的前驱节点。因为对于一个双子树的节点,他的前驱节点必然为左子树最大节点。
在这里再叙述一下如何查看一个节点的前驱节点和后继几点:
`前驱节点`:
`1 如果节点A有左子树,那么他的前驱节点为左子树中最大的节点。`
`2 如果节点A没有左子树,需要考察节点A的父节点,如果节点A是其父节点的右孩子,那么父节点为前驱节点,否则将父节点设置为当前节点A,继续向上查找,直到找到某个节点为其父节点的右孩子,这个父节点就是要找的前驱节点。`
`后继节点`:
`1 如果节点A有右子树,那么他的后继节点为其右子树的最小节点。`
`2 如果节点A没有右子树,那么同样遍历其父节点,找到某个节点是其父节点的左孩子,那么这个父节点就是要找的后继节点。`
如图
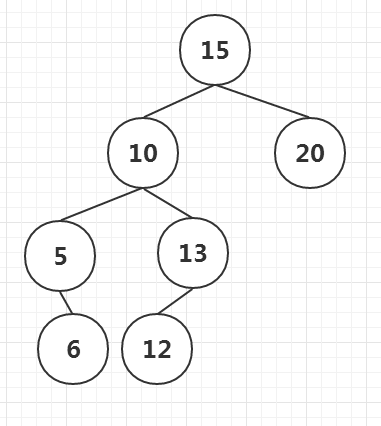
节点10的后继节点为12,为其右子树中最小的节点。
节点10的前驱节点为6,为其左子树中最大的节点。
节点12的前驱节点为10,因为节点12没有左子树,父节点为13,12不是13的右节点,需要继续向上查找,找到节点10,13是10的右节点,节点10为12的前驱节点。
节点6的后继节点为10,同样是向父节点找,直到找到某个节点是其父节点的左子树,5是10的左子树,所以10为6的后继节点。
节点5的前驱节点为NULL,因为节点5没有左子树,所以向上查找,直到找到根节点也不满足右节点的规则,所以节点5的前驱节点为NULL
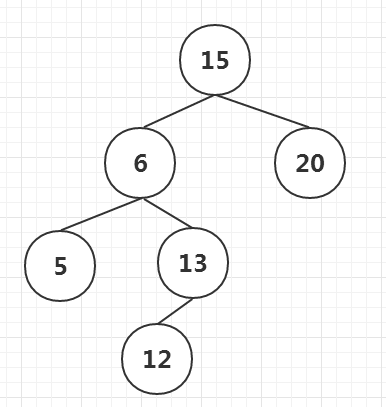
删除节点10,找到前驱节点6替换10,如果节点6有左子树,那么将左子树挂接到节点5的右节点。
如下图:
下面用代码实现上述插入,删除以及中序遍历的逻辑。
先实现树的节点
class TreeNode
{
public:
TreeNode():m_pParent(NULL), m_pLeftChild(NULL), m_pRightChild(NULL), m_nData(0){}
TreeNode(const TreeNode & tree){
this->m_nData = tree.m_nData;
this->m_pParent = NULL;
this->m_pLeftChild = NULL;
this->m_pRightChild = NULL;
}
TreeNode(int data):m_nData(data), m_pRightChild(NULL), m_pLeftChild(NULL), m_pParent(NULL){}
~TreeNode(){
this->m_nData = 0;
this->m_pLeftChild = NULL;
this->m_pParent = NULL;
this->m_pRightChild = NULL;
}
TreeNode& operator =(const TreeNode& treeNode)//赋值运算符
{
if (this != &treeNode)
{
this->m_pParent = treeNode.m_pParent;
this->m_pLeftChild = treeNode.m_pLeftChild;
this->m_pRightChild = treeNode.m_pRightChild;
this->m_nData = treeNode.m_nData;
}
return *this;
}
friend ostream & operator<<(ostream &out, TreeNode &obj)
{
out << " " << obj.m_nData <<" ";
return out;
}
TreeNode * m_pParent;
TreeNode * m_pLeftChild;
TreeNode * m_pRightChild;
int m_nData;
};
实现树类
class TreeClass
{
public:
TreeClass():m_pRoot(NULL){}
~TreeClass(){
if(!m_pRoot)
{
return;
}
//找到树的最小节点
TreeNode * treeNodeTemp = findMinNode(m_pRoot);
vector<TreeNode *> treenodeVec;
while(treeNodeTemp)
{
treenodeVec.push_back(treeNodeTemp);
treeNodeTemp = findNextNode(treeNodeTemp);
}
for(int i = 0; i < treenodeVec.size(); i++)
{
delete(treenodeVec[i]);
}
treenodeVec.clear();
m_pRoot = NULL;
}
void initial( list<int>& data);
void visitTree();
//搜索前继节点
TreeNode *findPreNode(TreeNode * treeNode);
//搜索后继节点
TreeNode * findNextNode(TreeNode * treeNode);
//寻找一个子树最小节点
TreeNode * findMinNode(TreeNode * root);
//寻找一个子树最大节点
TreeNode * findMaxNode(TreeNode * root);
//删除一个节点
void deleteTreeNode(TreeNode* treeNode);
//删除的节点没有子节点
void deleteNoChildNode(TreeNode * treeNode);
//删除的节点有一个子节点
void deleteOneChildNode(TreeNode * treeNode, TreeNode * childNode);
//删除节点有两个孩子,找到后继节点或者前驱节点替换即可,这里选择前驱节点
void deleteTwoChildNode(TreeNode * treeNode);
//用前驱节点替换当前节点
void preupdateNode(TreeNode * preNode, TreeNode * treeNode);
void eraseNode(int i);
TreeNode * findTreeNode(int i);
TreeNode * m_pRoot;
};
有几个函数需要着重说明一下:
初始化函数,通过列表初始化为一棵树
void TreeClass::initial( list<int>& data)
{
for( list<int>::iterator listIter = data.begin(); listIter != data.end();
listIter++)
{
TreeNode * treeNode = m_pRoot;
if(!treeNode)
{
m_pRoot = new TreeNode(*listIter);
continue;
}
TreeNode * nodeParent = NULL;
bool findflag = true;
while(treeNode)
{
if(treeNode->m_nData < *listIter)
{
nodeParent = treeNode;
treeNode = treeNode->m_pRightChild;
}
else if(treeNode->m_nData > *listIter)
{
nodeParent = treeNode;
treeNode = treeNode->m_pLeftChild;
}
else
{
//找到树中有相等的节点,那么不插入,也可以完善为次数+1
findflag = false;
break;
}
}
if(findflag)
{
if(nodeParent->m_nData <*listIter )
{
TreeNode * treeNodeTemp =new TreeNode(*listIter);
nodeParent->m_pRightChild = treeNodeTemp;
treeNodeTemp->m_pParent = nodeParent;
}
else
{
TreeNode * treeNodeTemp =new TreeNode(*listIter);
nodeParent->m_pLeftChild = treeNodeTemp;
treeNodeTemp->m_pParent = nodeParent;
}
}
}
}
中序遍历
//中序遍历
void TreeClass::visitTree()
{
if(!m_pRoot)
{
cout << "empty tree!!!";
}
//找到树的最小节点
TreeNode * treeNodeTemp = findMinNode(m_pRoot);
while(treeNodeTemp)
{
cout << (*treeNodeTemp);
treeNodeTemp = findNextNode(treeNodeTemp);
}
}
查找一个子树中最小节点
//寻找一个子树最小节点
TreeNode * TreeClass::findMinNode(TreeNode * root)
{
if(!root)
{
return NULL;
}
TreeNode * treeNode = root;
while(treeNode->m_pLeftChild)
{
treeNode = treeNode->m_pLeftChild;
}
return treeNode;
}
查找一个子树中最大节点
TreeNode * TreeClass::findMaxNode(TreeNode * root)
{
if(!root)
{
return NULL;
}
TreeNode * treeNode = root;
while(treeNode->m_pRightChild)
{
treeNode = treeNode->m_pRightChild;
}
return treeNode;
}
查找一个节点前驱节点
//搜索前驱节点
TreeNode* TreeClass::findPreNode(TreeNode * treeNode)
{
//左子树不为空,找到左子树中最大节点
if( treeNode->m_pLeftChild )
{
TreeNode * treeNodeTemp = findMaxNode( treeNode->m_pLeftChild);
return treeNodeTemp;
}
//左子树为空
//找到父节点,如果该节点是父节点的右孩子,那么父节点为前驱节点。
//如果不满足,则将父节点设为该节点,继续向上找,知道满足条件或者父节点为空
TreeNode * treeNodeTemp = treeNode->m_pParent;
while(treeNodeTemp && treeNode != treeNodeTemp->m_pRightChild)
{
treeNode = treeNodeTemp;
treeNodeTemp = treeNodeTemp ->m_pParent;
}
return treeNodeTemp;
}
查找一个节点的后继节点
//搜索后继节点
TreeNode * TreeClass::findNextNode(TreeNode * treeNode)
{
//右子树不为空,找到右子树中最小节点
if( treeNode->m_pRightChild )
{
TreeNode * treeNodeTemp = findMinNode( treeNode->m_pRightChild);
return treeNodeTemp;
}
//右子树为空
//找到父节点,如果该节点是父节点的左孩子,那么父节点为后继节点。
//如果不满足,则将父节点设为该节点,继续向上找,直到满足条件或者父节点为空
TreeNode * treeNodeTemp = treeNode->m_pParent;
while(treeNodeTemp && treeNode != treeNodeTemp->m_pLeftChild)
{
treeNode = treeNodeTemp;
treeNodeTemp = treeNodeTemp ->m_pParent;
}
return treeNodeTemp;
}
根据数据查找某个节点
TreeNode * TreeClass::findTreeNode(int i)
{
TreeNode *treeNode = m_pRoot;
while(treeNode)
{
if(treeNode->m_nData > i)
{
treeNode = treeNode->m_pLeftChild;
}
else if(treeNode->m_nData < i)
{
treeNode = treeNode->m_pRightChild;
}
else
{
return treeNode;
}
}
return treeNode;
}
某个节点有两棵子树,删除这个节点,函数如下:
void TreeClass::deleteTwoChildNode(TreeNode * treeNode)
{
//找到前驱节点
TreeNode* preNode = findPreNode(treeNode);
preupdateNode(preNode, treeNode);
delete(treeNode);
}
详细的删除和替换细节:
void TreeClass::preupdateNode(TreeNode * preNode, TreeNode * treeNode)
{
preNode->m_pRightChild = treeNode->m_pRightChild;
treeNode->m_pRightChild->m_pParent = preNode;
//判断前驱节点是否为该节点的左孩子
if(treeNode->m_pLeftChild != preNode)
{
TreeNode * prechild = NULL;
if(preNode->m_pLeftChild)
{
prechild = preNode->m_pLeftChild;
}
preNode->m_pLeftChild = treeNode->m_pLeftChild;
treeNode->m_pLeftChild->m_pParent = preNode;
if(preNode->m_pParent->m_pLeftChild == preNode)
{
preNode->m_pParent->m_pLeftChild =prechild;
if(prechild)
{
prechild->m_pParent = preNode->m_pParent;
}
}
else
{
preNode->m_pParent->m_pRightChild =prechild;
if(prechild)
{
prechild->m_pParent = preNode->m_pParent;
}
}
}
if(treeNode->m_pParent == NULL)
{
preNode->m_pParent = NULL;
m_pRoot = preNode;
return;
}
//节点有父节点,需要将父节点和前驱节点绑定
preNode->m_pParent = treeNode->m_pParent;
if(treeNode->m_pParent->m_pLeftChild == treeNode)
{
treeNode->m_pParent->m_pLeftChild = preNode;
}
else
{
treeNode->m_pParent->m_pRightChild = preNode;
}
}
如果节点没有子树,那么直接删除,如果节点有一颗子树,那么用该子树替代这个节点即可。
代码下载地址:
https://github.com/secondtonone1/searchtree
测试代码:
int array[6]={7,4,2,5,3,8};
list<int> mylist;
mylist.insert(mylist.end() , array ,array+6);
TreeClass treeClass;
treeClass.initial(mylist);
treeClass.visitTree();
cout << endl;
treeClass.eraseNode(7);
treeClass.visitTree();
cout << endl;
treeClass.eraseNode(4);
treeClass.visitTree();
cout << endl;
int array2[5]={7,4,2,5,8};
list<int> mylist2;
mylist2.insert(mylist2.end() , array2 ,array2+5);
TreeClass treeClass2;
treeClass2.initial(mylist2);
treeClass2.visitTree();
cout << endl;
treeClass2.eraseNode(4);
treeClass2.visitTree();
cout << endl;
int array3[6]={7,4,2,6,5,8};
list<int> mylist3;
mylist3.insert(mylist3.end() , array3 ,array3+6);
TreeClass treeClass3;
treeClass3.initial(mylist3);
treeClass3.visitTree();
cout << endl;
treeClass3.eraseNode(7);
treeClass3.visitTree();
cout << endl;
getchar();
return 0;
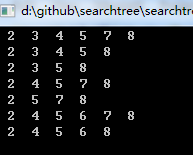
打印输出:
我的公众号谢谢关注:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号