【编程之美】高效率的安排见面会
一,题目
在校园招聘的季节里,为了能让学生们更好地了解微软亚洲研究院各研究组的情况,HR部门计划为每一个研究组举办一次见面会,让各 个研究组的员工能跟学生相互了解和交流。已知有n位学生,他们分别对m个研究组中的若干个感兴趣。为了满足所有学生的要求,HR希望每 个学生都能参加自己感兴趣的所有见面会。如果每个见面会的时间为t,那么,如何安排才能够使得所有见面会的总时间最短? 最简单的办法,就是把m个研究组的见面会时间依次排开,那我们就要用m * t的总时间,我们有10多个研究小组,时间会拖得很长,能否进一步提高效率?
二,分析
此题的官方解法是将问题转化为一个已知的图的问题:即图的最少着色问题。 但有两点感觉不太好:
- 一是这个问题的转换感觉角度有些大,不够平滑。 如果此前没听过图的最少着色问题,那么是怎么也不可能想到这儿的。
- 二是关于此题的分析与解法讲解非常笼统,尤其是解法,寥寥数语就完了 - 我觉得是没有把问题讲清楚的 - 虽然读者自己可以阅读“ 图的最少着色问题”来获得更多的了解,但既然此题作为单独的一题存在,我觉得还是讲清楚点好。
另外,自己思考了一下,觉的此题不转化成图的最少着色问题,通过简单的递归,应该也是可以实现的。
思路分析:
已知有n位学生,m个见面会,且每个学生可以选择参加任意多个见面会。我们的目的是在没有冲突的情况下把某几个见面会的时间重叠起来,同时开。何为冲突,比如学生甲参加了见面会A与B,那么A与B就是冲突的,因为如果同时开的话,学生甲必然要放弃一个。
那么,我们可以按以下方式,逐个考虑见面会:
- 对于见面会A,因为其前面没有见面会,略过;
- 对于见面会B,考虑它和其前面的见面会A是否冲突,如果不冲突,就将B和A合并,继续考虑C;而另外还有一个分支是不管是否冲突,此时不做合并,直接考虑C;
- 对于见面会C,考虑它和其前面的见面会A,B是否冲突,第一个分支是如果与A不冲突, 就将C和A合并,继续考虑D;第二个分支是如果与B不冲突, 就将C和B合并,继续考虑D;而第三格分支还是不做任何合并,直接考虑D
- 按此规则继续对下一个见面会做考察
- 当对最后一个招聘会做完考察后,记下其时间,程序然后递归回溯,会由其他分支继续考察最后一个招聘会,比较并记录最短的那个,这样,当所有的分支都考察过后,记录的那个最短时间就是全局最短的时间了。
代码
- 输入数据可以用一个二维数组input[m][n]来表示,行表示见面会,列表示学生,数组元素表示某学生是否参加该见面会。
- 递归过程用当前考虑的见面会控制,当最后一个见面会考虑完之后,就得到一个候选解,程序然后回溯,从另一分支再次进入,考虑最后一个见面会,与之前的候选解比较,保存较优的那个:候选解包括见面会时间与当前的具体安排
复杂度分析:
可以注意到,我们需要逐个考虑见面会,一共是m个;而在考虑第i个见面会时,我们最多可能会产生出i个分支,不难看出,总问题的规模为m!;
而产生每个分支时需要做的计算是O(n)的冲突检测与合并,于是,整个的算法复杂度为:O(m! * n)
#include <iostream>
2 #include <list>
3 #include <vector>
4
5 using namespace std;
6
7 // If 2 recruiting meetings are conflicting
8 bool IsConflict(const vector<bool>& v1, const vector<bool>& v2)
9 {
10 for(int i = 0; i < v1.size(); ++i)
11 {
12 if(v1[i] && v2[i]) return true;
13 }
14 return false;
15 }
16
17 // merge 2 recruiting meetings: v2 will be held at the same time of v1
18 void Merge(vector<bool>& v1, const vector<bool>& v2)
19 {
20 for(int i = 0; i < v1.size(); ++i)
21 {
22 v1[i] = v1[i] || v2[i];
23 }
24 }
25
26 // input: input[m][n], 2d array to represents students' selection of meetings.
row stands for meetings, column stands for students,
27 // and array value stands for if a student select a meeting
28 // next: The meeting to check
29 // curTime: Time required so far
30 // curArrangement: record the information of which meeting is merged with another
meeting
31 // best[output]:The best time
32 // bestArrangement[output] : The best arragement
33 void ArrangeRecruitings(vector<vector<bool> >& input, int next,
int& curTime, vector<list<int> >& curArrangement, int& bestTime,
vector<list<int> >& bestArrangement)
34 {
35 int m = input.size();
36 // base cases
37 if(next >= m)
38 {
39 // Save the best one
40 if(curTime < bestTime)
41 {
42 bestTime = curTime;
43 bestArrangement = curArrangement;
44 }
45
46 return;
47 }
48 else
49 {
50 // recursive cases
51 for(int i = 0; i <= next; ++i)
52 {
53
54 if(curArrangement[i].empty()) continue; // if already merged with other ones, just skip it
55
56 if (!IsConflict(input[i], input[next]))
57 {
58
59 // update the status
60 vector<bool> bkI = input[i];
61 Merge(input[i], input[next]);
62
63 curArrangement[next].pop_back();
64 curArrangement[i].push_back(next);
65
66 // Consider next one after merge
67 ArrangeRecruitings(input, next+1, curTime, curArrangement, bestTime, bestArrangement);
68
69 // restore the status
70 curArrangement[i].pop_back();
71 curArrangement[next].push_back(next);
72
73 input[i] = bkI;
74 }
75 }
76
77 // Consider next one without any merge
78 ArrangeRecruitings(input, next+1, ++curTime, curArrangement, bestTime, bestArrangement);
79
80 }
81 }
82
83
84 int main()
85 {
86 // 1. Initializing
87 int m = 3;
88 int n = 4;
89
90 vector<vector<bool> > input(m, vector<bool>(n, false));
91
92 input[0][0] = true;
93 input[0][1] = true;
94
95 input[1][1] = true;
96 input[1][2] = true;
97
98 input[2][2] = true;
99 input[2][3] = true;
100
101 //input[0][2] = true;
102
103 int curTime = 1;
104 int bestTime = m+1;
105 vector<list<int> > curArrangement(m);
106 vector<list<int> > bestArrangement(m);
107 for(int i = 0; i < m; ++i) curArrangement[i].push_back(i);
108
109 // 2. Solve
110 ArrangeRecruitings(input, 1, curTime, curArrangement, bestTime, bestArrangement);
111
112 // 3. Output the result
113 cout << "Totoal Time: " << bestTime << endl;
114 for(int i = 0; i < m; ++i)
115 {
116 cout << i << "): ";
117 if(bestArrangement[i].empty())
118 {
119 cout << "none" << endl;
120 continue;
121 }
122 for(list<int>::const_iterator it = bestArrangement[i].begin(); it != bestArrangement[i].end(); ++it)
123 cout << *it << "-";
124
125 cout << endl;
126 }
127 }
三,第二种解决方法
寻找活动集合S的最大相互兼容集合的方法[2],在《算法导论》贪心算法一章中有详细的讲解。解决此问题的具体步骤可总结为:
1)把面试集合S中的元素按其结束时间的递增顺序排列;
2)求其最大相互兼容面试集合M,并从原始集合S中删除之;
3)求集合S-M的最大相互兼容面试集合Q,并从集合S-M中删除之。重复此过程直到原始面试集合S中为空集为止;
4)统计求出的最大相互兼容面试集合的个数,即是面试集合S所需的最少面试点个数。
以上面的面试集合S为例,上述步骤用图像表示如下:每个图中用矩形框起来的面试为所属集合的最大相互兼容集合,一共有5个,即至少需要5个面试点。


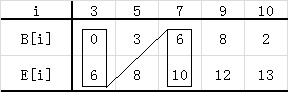
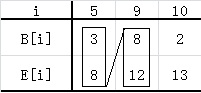

四,扩展问题一:
实际上就是求区间的最大重叠次数。书上P57的算法,比较巧妙,但要注意的是:排序时要用到双关键字比较,当两个值相等时,属于时间段开始的一定要排在属于时间段结束的后面,只有这样才能保证结果的正确性。(假设[3, 4)和[4, 5)能在同一个地方举行。书上区间段都是用闭区间,本文采用前闭后开。)
考虑到面试安排的时间一般安排在某个整点、半点或者某刻,可以采用计数的方法,如果都安排在整点,每处理一个区间[a, b),就对[a, b)间的所有整数计数一次。最后从计数结果中找出最大值即可。时间复杂度为O(n)(准确的讲,应该是O(k*n),k为区间的最大间隔,k<=24)。如果面试安排时间在某个半点、刻,可以对原来的时间乘以一个整数(比如2或4,这实际上就是桶排序设置桶间隔为0.5或0.25)。
//arr[][0]为面试开始时间,arr[][1]为面试结束时间
int max_places (int arr[][2], size_t sz)
{
if (arr==NULL || sz<1) return 0;
const size_t MAX_HOURS=24;
int count[MAX_HOURS]={0};
int max=0, j=0;
size_t i=0;
for (i=0; i<sz; ++i)
for (j=arr[i][0]; j<arr[i][1]; ++j) ++count[j];
for (i=0; i<MAX_HOURS; ++i)
if (count[i]>max) max=count[i];
return max;
}




