个人总结
加速输入输出
ios::sync_with_stdio(false);
x保留n位小数(头文件iomanip)
cout<<fixed<<setprecision(n)<<x;
读入一行
getline(cin,s);
set容器的查找
if(se.find(s)==se.end()) //代表se中没找到s
容器内二分查找
lower_bound(a,a+n,x)-a;//大于等于x的第一个值的下标 upper_bound(a,a+n,x)-1;//大于x的~
全排列
next_permutation(a,a+n);
位运算
x=(x+1)&x; //消除尾连续1 x=x&(-x); //最低位1的位置
快速幂
int pow(int a, int b) { int x=1; while(b) { if(b%2) x*=a; a*=a; b/=2; } return x; }
扩展欧几里得
int exgcd(int a,int b,int &x,int &y) { if(b==0){ x=1; y=0; return a;} int r=exgcd(b,a%b,x,y); int t=x; x=y; y=t-a/b*y; return r; }
欧拉函数
void init() { for(int i=1;i<=n;i++) e[i]=i; for(int i=2;i<=n;i++) if(e[i]==i) for(int j=i;j<=n;j+=i) e[j]=e[j]/i*(i-1); }
深度优先搜索
简单来说分3步:标记,向下搜索,标记还原。

#include<iostream>//洛谷普及练习场-深度优先搜索-迷宫 using namespace std; int m,n,sx,sy,ex,ey,t,cnt; int map[10][10]; int move[4][2]={-1,0,1,0,0,-1,0,1}; void dfs(int x,int y) { int dx,dy; if(x==ex&&y==ey){ cnt++; return;} for(int i=0;i<4;i++) { dx=x+move[i][0]; dy=y+move[i][1]; if((!map[dx][dy])&&dx>=1&&dx<=n&&dy>=1&&dy<=m) { map[dx][dy]=1; dfs(dx,dy); map[dx][dy]=0; } } } int main() { cin>>n>>m>>t>>sx>>sy>>ex>>ey; for(int i=0;i<t;i++){ int x,y; cin>>x>>y; map[x][y]=1;} map[sx][sy]=1; dfs(sx,sy); cout<<cnt; return 0; }
广度优先搜索
借助队列,判重。

#include<iostream>//洛谷普及练习场-广度优先搜索-01迷宫 #include<queue> #include<vector> using namespace std; struct point{ int x,y; char c; }; char s[1005][1005]; int n,m,cnt[1005][1005],vis[1005][1005],move[4][2]={-1,0,1,0,0,1,0,-1}; queue<point> q; vector<point> v; void bfs(int x,int y) { point p; p.x=x; p.y=y; p.c=s[x][y]; int t=0; q.push(p); vis[p.x][p.y]=1; while(!q.empty()) { point pp=q.front(); for(int i=0;i<4;i++) { p.x=pp.x+move[i][0]; p.y=pp.y+move[i][1]; if(p.x>=0&&p.x<n&&p.y<n&&p.y>=0&&!vis[p.x][p.y]) { p.c=s[p.x][p.y]; if((p.c^pp.c)!=0){ q.push(p); vis[p.x][p.y]=1;} } } v.push_back(pp); t++; q.pop(); } for(int i=0;i<v.size();i++) cnt[v[i].x][v[i].y]=t; v.clear(); } int main() { cin>>n>>m; for(int i=0;i<n;i++) for(int j=0;j<n;j++) cin>>s[i][j]; for(int i=0;i<n;i++) for(int j=0;j<n;j++) if(!vis[i][j]) bfs(i,j); while(m--){ int x,y; cin>>x>>y; cout<<cnt[x-1][y-1]<<endl;} return 0; }
动态规划
核心就是推状态转移方程。
01背包 当前容量放或不放,可用一维数组优化,第二重循环从后到前。
完全背包 同上,第二重循环从前到后。

#include<iostream>//洛谷普及试炼场-动态规划的背包问题-采药 #include<algorithm> using namespace std; int dp[1005]; int main() { int t,n; cin>>t>>n; for(int i=1;i<=n;i++) { int a,b; cin>>a>>b; for(int j=t;j>=a;j--) dp[j]=max(dp[j],dp[j-a]+b); } cout<<dp[t]; return 0; } #include<iostream>//洛谷普及试炼场-动态规划的背包问题-疯狂的采药 #include<algorithm> using namespace std; int dp[100005]; int main() { int t,m; cin>>t>>m; for(int i=1;i<=m;i++) { int a,b; cin>>a>>b; for(int j=a;j<=t;j++) dp[j]=max(dp[j],dp[j-a]+b); } cout<<dp[t]; return 0; }
不一一例举,具体题目得具体分析。
图论
本菜鸡就写过一次并查集及dijkstra,比赛碰到图论应该会直接放弃。

#include<iostream>//洛谷普及试炼场-普及常见模板-并查集 using namespace std; int a[10005]; int find(int k) { int kk=k,i; while(kk!=a[kk]) kk=a[kk]; while(k!=a[k]){ i=k; k=a[k]; a[i]=kk;} return kk; } int main() { int n,m; cin>>n>>m; for(int i=1;i<=n;i++) a[i]=i; while(m--) { int x,y,z; cin>>z>>x>>y; if(z==1) a[find(x)]=find(y); if(z==2){ if(find(x)==find(y)) cout<<'Y'<<endl; else cout<<'N'<<endl;} } return 0; }

#include<iostream>//洛谷普及练习场-普及常见模板-单源最短路径 #include<queue> #include<algorithm> #define inf 2147483647 using namespace std; struct edge{ int u,v,w,next; }; struct point{ int h,dis; }; bool operator<(point a,point b) { return a.dis>b.dis; } int n,m,s,dis[100005],head[500005],vis[100005]; edge e[500005]; priority_queue<point> q; void dijkstra() { point p; p.h=s; p.dis=0; q.push(p); while(!q.empty()) { p=q.top(); q.pop(); if(!vis[p.h]) { vis[p.h]=1; for(int i=head[p.h];i;i=e[i].next) { int v=e[i].v; dis[v]=min(dis[v],dis[p.h]+e[i].w); point pp; pp.h=v; pp.dis=dis[v]; q.push(pp); } } } } int main() { cin>>n>>m>>s; for(int i=1;i<=n;i++) dis[i]=i==s?0:inf; for(int i=1;i<=m;i++){ cin>>e[i].u>>e[i].v>>e[i].w; e[i].next=head[e[i].u]; head[e[i].u]=i;} dijkstra(); for(int i=1;i<=n;i++) cout<<dis[i]<<" "; return 0; }
KMP
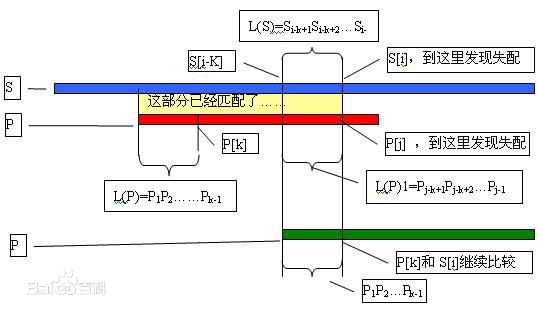

#include<iostream> #include<cstring> #include<cstdio> using namespace std; int next[1000005]; char s1[1000005],s2[1000005]; void kmp_pre(char x[],int m) { int i,j; j=next[0]=-1; i=0; while(i<m){ while(-1!=j && x[i]!=x[j])j=next[j]; next[++i]=++j; } } void kmp(char x[],int m,char y[],int n){ int i,j; kmp_pre(x,m); i=j=0; while(i<n){ while(-1!=j && y[i]!=x[j])j=next[j]; i++;j++; if(j>=m){ cout<<i-j+1<<endl; j=next[j]; } } } int main() { cin>>s1>>s2; int l1=strlen(s1),l2=strlen(s2); kmp(s2,l2,s1,l1); for(int i=1;i<=l2;i++) cout<<next[i]<<" "; return 0; }
树状数组


#include<iostream>//洛谷提高历练地-提高模板nlogn数据结构-树状数组1 #define ll long long using namespace std; ll n,m,tv[1100000]; ll lowbit(ll x) { return x&(-x); } void add(ll x,ll k) { while(x<=n) { tv[x]+=k; x+=lowbit(x); } } ll sum(ll x) { ll res=0; while(x!=0) { res+=tv[x]; x-=lowbit(x); } return res; } int main() { ios::sync_with_stdio(false); cin>>n>>m; for(int i=1;i<=n;i++){ ll x; cin>>x; add(i,x);} while(m--) { ll t; cin>>t; if(t==1) { ll x,k; cin>>x>>k; add(x,k); } else if(t==2) { ll x,y; cin>>x>>y; cout<<sum(y)-sum(x-1)<<endl; } } return 0; }
线段树
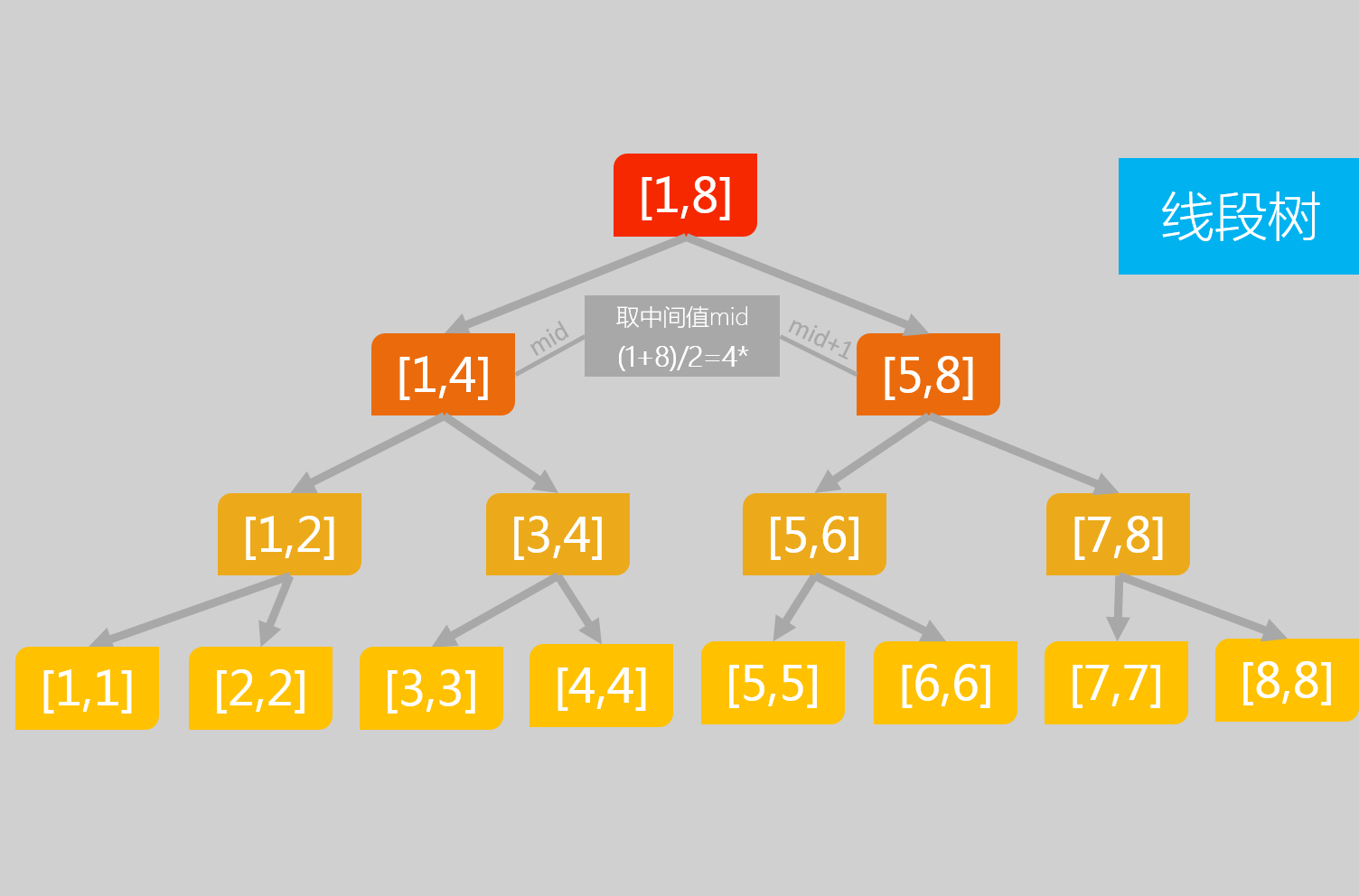

#include<iostream>//洛谷提高模板线段树1 #define ll long long using namespace std; ll n,m,a[100005],lt[410000],vis[410000]; void build(ll p,ll l,ll r) { if(l==r){ lt[p]=a[l]; return;} ll mid=(l+r)/2; build(p*2,l,mid); build(p*2+1,mid+1,r); lt[p]=lt[p*2]+lt[p*2+1]; } void push_down(ll p,ll l,ll r) { ll mid=(l+r)/2; vis[p*2]+=vis[p]; lt[p*2]+=vis[p]*(mid-l+1); vis[p*2+1]+=vis[p]; lt[p*2+1]+=vis[p]*(r-(mid+1)+1); vis[p]=0; } void update(ll x,ll y,ll l,ll r,ll p,ll k) { if(x<=l&&y>=r){ lt[p]+=k*(r-l+1); vis[p]+=k; return;} push_down(p,l,r); ll mid=(l+r)/2; if(x<=mid) update(x,y,l,mid,p*2,k); if(y>mid) update(x,y,mid+1,r,p*2+1,k); lt[p]=lt[p*2]+lt[p*2+1]; } ll query(ll x,ll y,ll l,ll r,ll p) { ll res=0; if(x<=l&&y>=r) return lt[p]; push_down(p,l,r); ll mid=(l+r)/2; if(x<=mid) res+=query(x,y,l,mid,p*2); if(y>mid) res+=query(x,y,mid+1,r,p*2+1); return res; } int main() { ios::sync_with_stdio(false); cin>>n>>m; for(int i=1;i<=n;i++) cin>>a[i]; build(1,1,n); while(m--) { ll t; cin>>t; if(t==1) { ll x,y,k; cin>>x>>y>>k; update(x,y,1,n,1,k); } else if(t==2) { ll x,y; cin>>x>>y; cout<<query(x,y,1,n,1)<<endl; } } return 0; }






