动态规划初步 刘汝佳字数 数字三角形
有一个由非负整数组成的三角形,第一行只有一个数,除了最下行之外每个数左下方和右下方各有一个数 如图所示
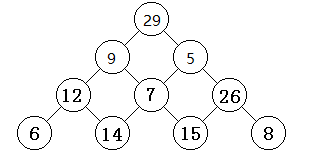
从第一行的数开始,每次可以往左下或右下走一格,直到走到最下行,把沿途经过的数全部加起来,如何走才能使得这个和最大?
分析:
一看到题目我们很自然的可以想到用回溯法(DFS)做,即每次都选择靠左的格子走,走到头后再回溯选择靠右的格子,按<左,右>的顺序遍历完所有的路径
代码如下:
#include<iostream> using namespace std; int a[11] = {0,29,9,5,12,7,26,6,14,15,8};//假设有四层 int max = -1, sum = 0; int shuzi(int i, int j)//计算第i层第j个的数字在a数组的第几个 { int x = 0; for (int l = 1; l <= i - 1; l++) { x += l; } x += j; return x; } int dfs(int i, int j) { if (i==5) { if (sum > max) max = sum; return 0; } sum += a[shuzi(i, j)]; dfs(i + 1, j); dfs(i + 1, j + 1); sum -= a[shuzi(i, j)]; return 0; } int main(int argc, char* argv[]) { dfs(1, 1); cout << max<<endl; return 0; }
时间复杂度是2^n,指数级的,n一旦大了就会超时
所以用状态转移方程来发现每项的依赖项
方程如下:
d(i,j)=a(i,j)+max{d(i+1,j),d(i+1,j+1)};
代码如下:
#include<iostream> using namespace std; int a[20] = {0,1,2,3,4,5,6,7,8,9,12,0,0,0,0,0,0,0,0,0}; int max(int a, int b) { return a > b ? a : b; } int shuzhi(int i, int j) { int x = 0; for (int l = 1; l <= i - 1; l++) { x += l; } x += j; return x; } int solve(int i, int j) { int x=shuzhi(i, j); return a[x]+(i==4?0:max(solve(i+1,j),solve(i+1,j+1))); } int main(int argc, char* argv[]) { cout << solve(1, 1)<<endl; return 0; }
已经知道了每项的依赖项,就可以避免重复计算
#include<iostream> using namespace std; int a[20] = {0,13,11,8,12,7,26,6,14,15,8}; int dp[10][10] = { {0,0} }; int max(int a, int b) { return a > b ? a : b; } int shuzi(int i, int j) { int x = 0; for (int l = 1; l <= i - 1; l++) { x += l; } x += j; return x; } int solve(int i, int j) { for (int k = 1; k <= 4; k++) dp[4][k] = a[shuzi(4, k)]; for (int k = 3; k >= 1; k--) for (int l = 1; l <= k; l++) dp[k][l] = a[shuzi(k, l)]+ max(dp[k + 1][l], dp[k + 1][l + 1]); return dp[i][j]; } int main(int argc, char* argv[]) { cout << solve(1, 1) << endl; return 0; }
简化版:
#include<iostream> using namespace std; int a[20] = { 0,1,2,3,4,5,6,7,8,9,10}; int dp[10][10] = { { 0,0 } }; int max(int a, int b) { return a > b ? a : b; } int shuzi(int i, int j) { int x = 0; for (int l = 1; l <= i - 1; l++) { x += l; } x += j; return x; } int solve(int i, int j) { if (dp[i][j] >= 0) return dp[i][j]; return a[shuzi(i, j)] + (i==4?0:max(solve(i+1,j), solve(i + 1, j+1))); } int main(int argc, char* argv[]) { memset(dp, -1, sizeof(dp)); cout << solve(1, 1) << endl; return 0; }


