编辑距离

第一章(判断子序列)

题目

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。

思路

在做这一题之前我做过一些公共子序列之类的题目,所以这一题的dp数组的含义比较容易考虑到:(dp[i][j]: 以s[i-1]结尾的s子序列与t[j-1]结尾的t子序列的最大公共子序列长度).

在确定了dp数组的定义后,递推公式的确定就比较容易了:

1. 在s.charAt(i-1)==t.charAt(j-1)时:
   dp[i][j]=dp[i-1][j-1]+1(即在前面的基础上的长度+1码,毕竟s[i-1],t[j-1]代表了正在考虑的元素,只要符合就在原先确定的长度上加1)
2. s.charAt(i-1)!=t.charAt(j-1)时:
   dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1])
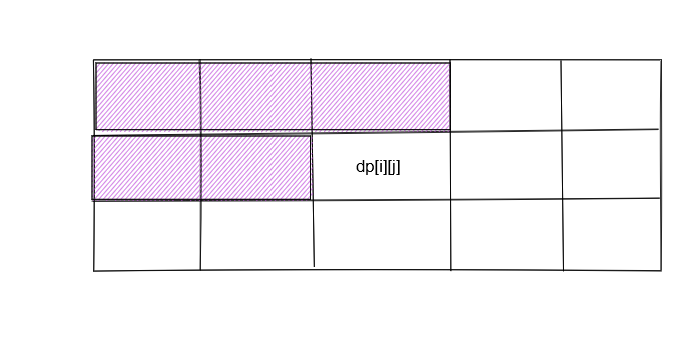
   原因如下:(回到dp的定义:dp[i][j]应该=以s[i-1]结尾的s子序列与t[j-1]结尾的t子序列的公共子序列长度,但是现在各自的最后一个元素不等,那就说明dp[i][j]只能取紫色部分中最大的,在dp中体现为max(dp[i-1][j],dp[i][j-1]),毕竟是一层一层推导出来的嘛,也就是题目中的删除操作)

代码如下:

public boolean isSubsequence(String s, String t) {
    //判断子序列
    //1.确定dp数组以及下标的含义
    //dp[i][j]代表以s[0~i-1],t[0~j-1]的最大公共子序列长度
    int [][]dp=new int[s.length()+1][t.length()+1];
    //这里初步设计删除操作
    //2.确定递推公式
    //if(s.charAt(i-1)==t.charAt(j-1))dp[i][j]=dp[i-1][j-1]+1;
    //else dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
    //3.初始化
    //dp[i][0]:0
    //dp[0][j]:0
    //4.遍历顺序
    for (int i = 1; i <dp.length; i++) {
        for (int j = 1; j < dp[0].length; j++) {
            if(s.charAt(i-1)==t.charAt(j-1)){
                dp[i][j]=dp[i-1][j-1]+1;
            }
            else dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
        }
    }
    return dp[s.length()][t.length()]==s.length();
}

回顾

在这一次的题目中认识到删除操作是通过dp数组定义:dp[i][j]: 以s[i-1]结尾的s子序列与t[j-1]结尾的t子序列的最大公共子序列长度,然后结合递推公式来推算出来的.
参考代码随想录