Basic Model（二）
论文列表
《Spectral Networks and Deep Locally Connected Networks on Graphs》
《Deep Convolutional Networks on Graph-Structured Data》
这两篇是同一个人提出来的
一个侧重理论模型，一个侧重实际应用
点击右下角的目录按钮可以选择想要看的文章
如果有疑问欢迎和我交流 QQ:1181852700
《Spectral Networks and Deep Locally Connected Networks on Graphs》
我现在看到Spectral就怕，因为而这个缠绕上就少不了傅里叶，拉普拉斯，而关于这两个可以展开的东西实在太多，而且都很难，但是面对这篇文章还是硬着头皮把主干内容看完了，毕竟困难是拿来克服的嘛哈哈哈
文章开头就花了大篇幅介绍卷积，卷积平移不变性、卷积的使用使得参数量大大减少等等优点，于是一个自然而然的想法应运而生——能不能将CNN的思想应用到图上来，但是直接用肯定不行——图片的大小你可以统一到同一尺度上去，但是图结构不行啊，考虑从卷积入手。就像处理声音一样，作者从两个角度去构造这个图神经网络：空间域和频率域
-
空间域：卷积卷积，在图里卷的是谁，怎么卷？
卷邻居节点。
说实话，上面的方程里各种符号说明都没有，\(\Omega\)也只是在前文提到是一个离散的点集合，可是在这里怎么就带括号了？恕我才疏学浅，只能理解为根据邻居的边权重，不是所有邻居都能用，要用阈值进行筛选
怎么卷？和卷积一样，用一个矩阵去乘
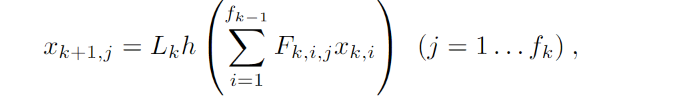
其中，fk表示第k层的数据维度，Fkij是一个dk-1 x dk-1的矩阵，j表示的是第k层的维度，你想设为多少就多少，就和卷积核的数量意义一样，Lk表示的是一个池化的操作
整体的结构如下图所示
-
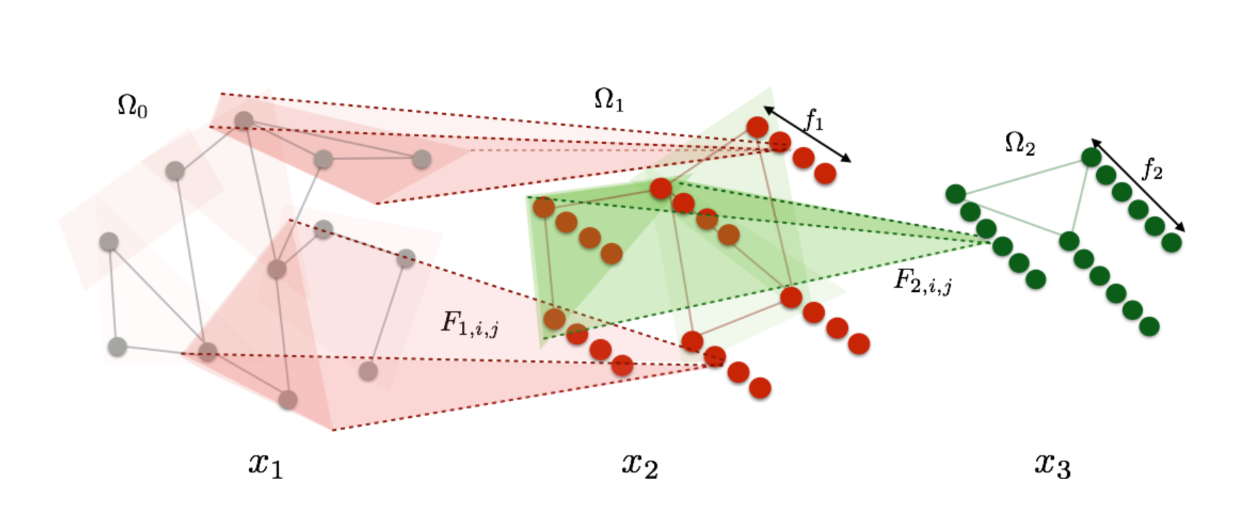
频率域
预备知识
离散域的卷积公式：\((f*g)=\sum_{\tau=-\infty}^{\infty}f(\tau)g(n-\tau)\)
离散傅里叶变换公式：\(X(k)=F(x(n))=\sum_{n=0}^{N-1}x(n)e^{-jk\frac{2\pi}{N}n},k\in[0,N-1]\)
离散傅里叶逆变换公式：\(x(n)=F^{-1}(X(k))=\frac{1}{N}\sum_{k=0}^{N-1}X(k)e^{jk\frac{2\pi}{N}n},n\in[0,N-1]\)
卷积公式的频域表达：\((f*g)=F^{-1}[F[f]\bigodot F[g]]\)（中间的点表示两个矩阵(或向量)的逐点乘积，即哈达玛乘积）
好了，具有以上知识你就能构造一个图卷积神经网络了。哈哈哈开玩笑，还有好长一段路要走。。
接下来要引入拉普拉斯矩阵\(L=D-W\)（论文里另一种形式是归一化的拉普拉斯矩阵），其中D表示度矩阵，对角线的元素是节点的度，W表示边的权重。
对L做一个矩阵分解得到\(L=V\Lambda V^T,V=(v_1,...,v_n)\)，其中vn表示L的特征向量，中间的大写λ是特征值矩阵。
并且具有如下性质\(Lv_i=λ_iv_i\)
此时，我们再引入一个方程——亥姆霍兹方程（Helmholtz Equation）
\(\nabla^2 f= \frac{\partial e^{jk\frac{2\pi}{N}n}}{\partial n^2}=-(k\frac{2\pi}{N})^2e^{-jk\frac{2\pi}{N}n}=-w^2f\)
将上面的式子和\(Lv_i\)的公式进行对比
\(e^{-jk\frac{2\pi}{N}n}\)对应\(v_i\)，\(-w^2\)对应\(\lambda_i\)，带入傅里叶变换公式，得到\(\hat{f}(k)=v_k^Tf\)，然后带入卷积公式得到（这里就省略了，公式太长，直接出结果了）
\((g*f)(n)=Vg_\theta V^Tf\)
此时再回过头看论文里给出的公式
中间的F和我们推导出来的gθ是不是很相似，没错，就是一模一样，至此，我们就可以在频域上面训练咯，因为有参数Fkij让我们训练
推导过程几乎都来自于这篇博文，其它博文都没讲过怎么推导，清一色都是一笔带过https://blog.csdn.net/weixin_43450885/article/details/105296033
至于实验，下面的图还是蛮惊艳的，但是其它图（第二张）就感觉不知所云了
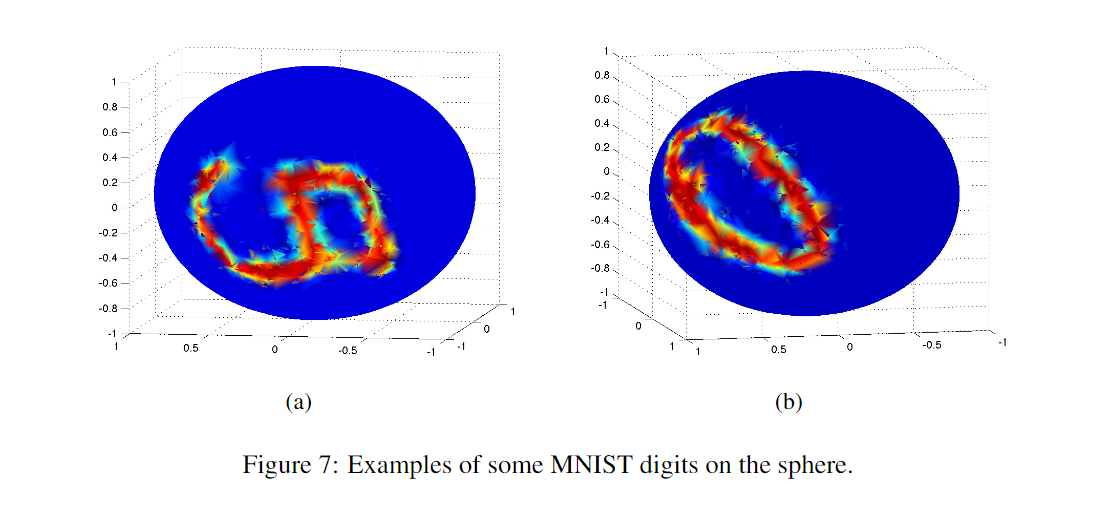
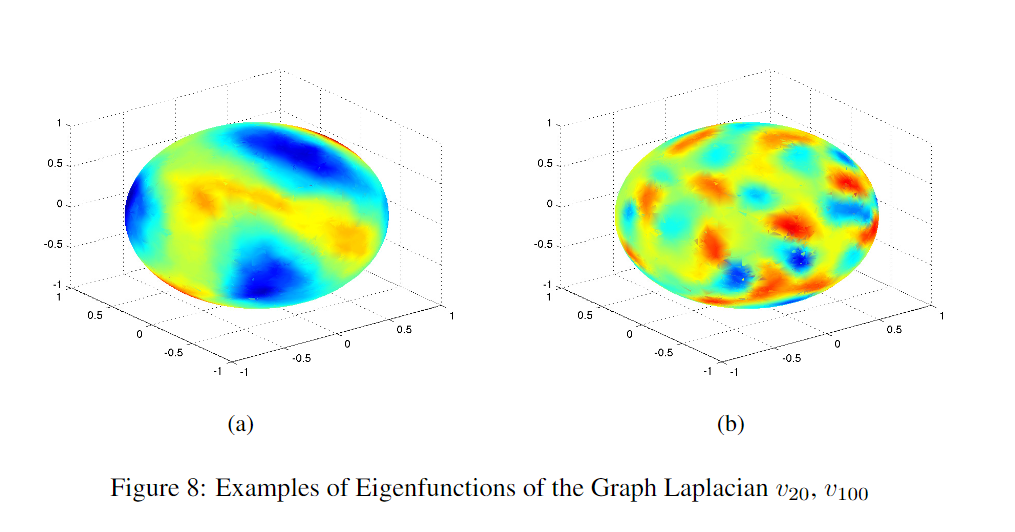
《Deep Convolutional Networks on Graph-Structured Data》
这篇文章是上一篇文章的延续，作者在频率域的实现模型进行了进一步改进，使得他能够适用于一些具有实际意义的问题。
作者在两个以前不可能应用卷积网络的应用领域探索图数据卷积方法：文本分类和生物信息学
U表示图傅里叶变换矩阵，K表示插值核（和核函数相关）
池化的方式：层次聚类
在搭建Spectral Network之前，作者说要从数据中估计相似度矩阵，学边的权重？
原话是：Whereas some recognition tasks in non-Euclidean domains, such as those considered in [2] or [12], might have a prior knowledge of the graph structure of the input data, many other real-world applications do not have such knowledge. It is thus necessary to estimate a similarity matrix W from the data before constructing the spectral network.
翻译过来就是：虽然非欧几里德域中的一些识别任务，如[2]或[12]中考虑的任务，可能事先知道输入数据的图形结构，但许多其他实际应用程序不具备这种知识。因此，在构造光谱网络之前，需要从数据中估计相似矩阵W
于是，又可以分为无监督情况和有监督情况下的权重学习
无监督学习的时候采用核函数度量距离
有监督学习的时候直接上MLP（另一种方法没看懂，就不放上来了）
