数据预处理
数据预处理
处理数据缺失
| 方法 | 具体措施 |
|---|---|
| 忽略 | 直接删除,简单粗暴,缺失数据少的时候很管用 |
| 手动填充 | 重新收集数据,需要某些领域的专业知识,可行性不高 |
| 自动填充 | 取中位数或者平均数 |
离群点检测 OUTLIER
世界之大,无奇不有,有时候明显和其他数据格格不入的数据,并不一定是错误的点,比如我们身边平时很少有身高超过2m的人,但是这是的的确确存在的。
尽管如此,我们在训练模型的时候为了更加符合常识,囊括更多的情况,就不能让这些点干扰我们的模型,此时这些点就被界定为“离群点”。
下面介绍课程中的一种算法:基于密度的局部离群点检测
定义
\(reachdistance_k(A,B)\):可达距离,理解为定义一个A到B的距离的度量即可
\(k-distance(B)\):对象B的第k领域距离
\(d(A,B)\):A点到B点的距离(可以是欧式距离)
\(reachdistance_k(A,B) = max\{k-distance(B),d(A,B)\}\)
\(lrd(A)=\frac{|N_kA|}{\sum_{B∈N_k(A)}reachdistance_k(A,B)}\)
\(N_k(A)\)表示临近点的集合
\(lrd(A)\)表示度量A点到相邻点的相近程度
单单看lrd(A)并不能得出什么,需要采用相对的概念对其进行描述
\(LOF_k(A) = \frac{\sum_{B∈N_k(A)}{\frac{lrd(B)}{lrd(A)}}}{{N_k(A)}}\)
如果A和相邻的点比较远,除了A点之外的点和它们各自的近邻比较近,相比之下A就可以被认为是一个离群点。
更多的参照这个博客:https://blog.csdn.net/mw21501050/article/details/75389267
重复数据判别
有时候,由于网络原因,客户可能重复提交数据,导致数据库中出现相同的数据,又或者同名同姓的人在同一个数据库中提交了记录。这些情况都要视各个领域的不同而具体制定不同的处理方案。
对于简单的完全重复数据,可以采用滑动窗口的方法对其进行剔除。但是这是基于重复的数据互相挨得很近的假设,毕竟现在是大数据时代,对于如此海量的数据维持一个滑动窗口实在是不太可能。
数据类型编码
数据可以是连续的、离散的、抽象的、具体的,可以是文本数据,可以是音频数据,对于无法转换成数值数据的需要将他们进行编码,才可以导入模型进行计算。
one-hot 编码
区别于{low,media,high}这样的有序数据,更多的数据是像{医生、工程师、老师}这样的数据,数据类型之间是平等的,并不存在先后排名。
one-hot编码则是形成一个矩阵,每个特征作为单独的一列
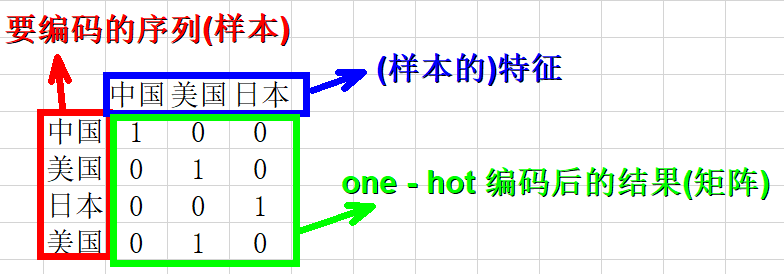
这种编码方式的缺点也很明显,特征维数高了之后矩阵的规模是巨大的。
数据采样
数据量很大时
受限于IO,读取所有的数据太费时费力,而且是不必要的,但是读取部分数据的同时又要保持数据的完整特征,才能保证训练出来的模型的正确性。
不平衡数据集
数据的不平衡指的是数据集中一种类别的样本远超另一种类别。
衡量不平衡度
\(G-mean = (Acc^{+} + Acc^{-})^{1/2}\)
其中\(Acc^{+}=\frac{TP}{TP+FN} ,Acc^{-}=\frac{TN}{TN+FP}\)
\(F-measure = \frac{2\times Precision\times Recall}{Precision + Recall}\)
其中\(Precision = \frac{TP}{TP+FP} ,Recall = \frac{TP}{TP+FN}\)
解决方案
SMOTE算法:手动生成较少的类的数据,一种简单的做法就是按照随机正态分布在每个点的周边生成点
描述数据
协方差、中位数、平均数、方差
数据可视化
见本人博客:https://www.cnblogs.com/seaman1900/p/15356531.html
特征选择
信息&熵&信息增益
往信息增益高的特征选择
参见我的博文:https://www.cnblogs.com/seaman1900/p/15314895.html
以随机森林剪枝为例:
搜索算法
模拟退火、贪心搜索、遗传算法
PCA——主成分分析
网课中省略了太多知识点,在这里进行一一详细说明
首先引入协方差
\(Cov(a,b)=\frac{1}{m-1}{\sum\limits_{i=1}^{m}(a_i-μ_a)(b_i-μ_b)}\)
一般来说,数据的处理需要去除平均值,也就使得
\(Cov(a,b)=\frac{1}{m-1}{\sum\limits_{i=1}^{m}(a_ib_i)}\)
对于协方差来说:
\(Cov(a,b)>0,a,b正相关\)
\(Cov(a,b)<0,a,b负相关\)
\(Cov(a,b)=0,a,b关系不确定\)
网课上还有一个难以理解的问题,突然给出了\(S(x)=\frac{1}{n-1}XX^T\)
现在看来豁然开朗,这个\(\frac{1}{n-1}\)来自于协方差,将上面的式子展开就可以得到一个协方差矩阵,同时也是对称阵,对角线上表示的是方差,下面以二维矩阵为例子展示:
\(\frac{1}{n-1}XX^T=\left[\begin{matrix}Cov(a,a)&Cov(a,b)\\Cov(b,a)&Cov(b,b)\end{matrix}\right]\)
联系协方差的特性,我们的目标和工具也就逐渐清晰起来:将一组 N 维向量降为 K 维,其目标是选择 K 个单位正交基,使得原始数据变换到这组基上后,各变量两两间协方差为 0(即除了对角线上的数,其他都尽量接近0即可),而变量方差则尽可能大(在正交的约束下,取最大的 K 个方差)
那么如何才能使得变换后的协方差尽可能小,方差尽可能大呢?
将这个问题转换为拉格朗日问题
我们给定原始矩阵\(X\)(去除过均值),给定变换之后的基为\(\omega\),变换后的坐标为\(X\omega\)样本的方差描述为(推导过程看这里:https://zhuanlan.zhihu.com/p/77151308)
\(D = \omega ^T (\frac{1}{n-1}XX^T) \omega\)
中间的不就是原样本的协方差矩阵嘛,列成拉格朗日问题的形式
\(\left\{\begin{matrix}max\{\omega ^T S \omega\} \\ s.t.\omega^T\omega =1\end{matrix}\right\}\)
\(L(\omega)=\omega ^TS\omega+\lambda(1-\omega ^T\omega)\)
对\(\omega\)进行求导,这里就涉及了矩阵求导的知识,这里列了一个表格可以快速查询:https://blog.csdn.net/a493823882/article/details/81324037
求导之后的值是:\(S\omega = \lambda\omega\)
此时\(D=\lambda\)
因此,\(X\)投影后的方差就是协方差矩阵的特征值。我们要找到最大方差也就是协方差矩阵最大的特征值,最佳投影方向就是最大特征值所对应的特征向量,次佳就是第二大特征值对应的特征向量,以此类推
求解步骤
设有 m 条 n 维数据。
- 将原始数据按列组成 n 行 m 列矩阵 X;
- 将 X 的每一行进行零均值化,即减去这一行的均值;
- 求出协方差矩阵\(C = \frac{1}{n-1}XX^T\);
- 求出协方差矩阵的特征值及对应的特征向量;
- 将特征向量按对应特征值大小从上到下按行排列成矩阵,取前 k 行组成矩阵 P;
- \(Y=PX\)即为降维到 k 维后的数据。
LDA——线性判别分析
区别于PCA,LDA是无监督的降维技术,中心思想:投影后类内方差最小,类间方差最大
二类LDA——分两类
我们定义
\(\mu_i=\frac{1}{N_j}\sum\limits_{x∈X_j}x(i=0,1)\)
表示同类数据的中心点的距离
\(\sum_j=\sum\limits_{x∈X_j}(x-\mu_j)(x-\mu_j)^T(j=0,1)\)
表示同一类别数据的散度
由于LDA需要让不同类别的数据的类别中心之间的距离尽可能的大,也就是我们要最大化\(||\omega ^T\mu_0-\omega^T\mu_1||_2^2\),同时我们希望同一种类别数据的投影点尽可能的接近,也就是要同类样本投影点的协方差\(\omega^T\sum_j\omega\)尽可能的小,即最小化\(\omega^T\sum_0\omega+\omega^T\sum_1\omega\)
因此定义一个数用来描述我们的优化目标:
\(J(\omega)=\frac{||\omega ^T\mu_0-\omega^T\mu_1||_2^2}{\omega^T\sum_0\omega+\omega^T\sum_1\omega}=\frac{\omega^T(\mu_0-\mu_1)(\mu_0-\mu_1)^T\omega}{\omega^T(\sum_0+\sum_1)\omega}\)
为了简化计算,定义类内散度矩阵
\(S_\omega=(\sum_0+\sum_1)\)
同时定义类间散度矩阵
\(S_b=(\mu_0-\mu_1)(\mu_0-\mu_1)\)
简化之后的东西又叫做广义瑞利熵,根据这个东西的性质可以求得,有能力还可以直接求导获得
\(\omega = S_\omega ^{-1}(\mu_0-\mu_1)\)
具体分析过程见这个博客:https://www.cnblogs.com/pinard/p/6244265.html
LDA流程
输入:数据集\(D={(x1,y1),(x2,y2),...,(x_m,y_m)}\),其中任意样本\(x_i\)为\(n\)维向量,\(y_i∈\{C1,C2,...,Ck\},y_i∈\{C_1,C_2,...,C_k\}\),降维到的维度\(d\)。
输出:降维后的样本集\(D′\)
-
计算类内散度矩阵\(S_\omega\)
-
计算类间散度矩阵\(S_b\)
-
计算矩阵\(S^{−1}_wS_b\)
4)计算\(S^{−1}_wS_b\)的最大的\(d\)个特征值和对应的\(d\)个特征向量\((w_1,w_2,...w_d)\),得到投影矩阵\(W\)
-
对样本集中的每一个样本特征\(x_i\),转化为新的样本\(z_i=W^Tx_i\)
-
得到输出样本集\(D′={(z1,y1),(z2,y2),...,(zm,ym)}\)

