浅谈爬山算法/模拟退火
提到随机化，我们就不能不提大名鼎鼎的爬山算法和模拟退火了
爬山算法
什么是爬山算法？
考虑我们将每种状态所对应的结果视作一个函数
可以得到一个函数图像
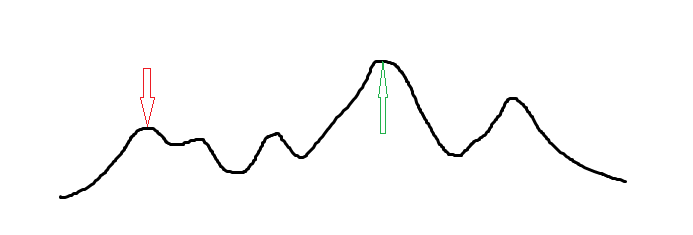
对于当前的一个状态，我们每次随机一个临近的状态，看是否更优，如果更优就跳过去，否则原地不动
同时，我们有一个温度参数，这个温度会不断降低，而每次随机的区间范围会随着温度不断降低而渐渐缩小
直到最后温度小到一定程度就结束爬山
整体流程如下
while(1)
{
if(温度<结束温度)
{
break;
}
随机一个临近状态;
得到这个状态的函数值;
if(更优)
{
答案状态=临近状态;
}
温度*=降温系数;
}
但是很显然的，爬山算法很容易陷入到一个局部最优解之中出不来，正如上图红色箭头所示
所以，爬山算法适用于单峰函数
另外有时获取临近状态的范围受温度的影响这一部分可能很难实现，所以可以不管，但是这样的效果会差一些
为了解决爬山算法的这些问题，模拟退火就出场了
模拟退火
什么是退火
退火，指的是将金属缓慢加热到一定温度，保持足够时间，然后以适宜速度冷却，在这个过程中，金属原子的热运动逐渐减弱，会逐渐趋向于一个稳定的状态。
退火可以使材料拥有更好的性能
而模拟退火，顾名思义，就是模拟 退火 这一过程
先用一句话概括：如果新状态的解更优则修改答案，否则以一定概率接受新状态。
模拟退火和爬山算法相比，多了一个接受以一定概率接受劣解的过程
同样有一个初温 \(T_0\) 终止温度为 \(T_e\) 降温系数为 \(d\) ,当前温度为 \(T\)
根据物理学知识
我们接受一个劣界的概率应该是
\[{\LARGE e^{\frac{- \Delta E}{T} } }
\]
这个函数再指数 \(<0\) 时 会得到一个 \(<1\) 的数
这个可以使用 STL 提供的 exp() 函数实现
流程大致如下
while(1)
{
if(温度<结束温度)
{
break;
}
随机一个临近状态;
得到这个状态的函数值;
if(更优)
{
答案状态=临近状态;
}
else
{
以一定概率接受劣解
}
温度*=降温系数;
}
由于模拟退火有概率接受劣解，所以能够跳出局部最优解的不足，在多峰函数上有更好的表现
举个例子，对于 P3878分金币
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define rand() rnd(0,RAND_MAX)
mt19937 eng;
int rnd(int l,int r)
{
return l+(eng()%(r-l+1));
}
int rnd()
{
return eng();
}
double cool_=0.9912,Ts=1e4,T0=1e-7;
ll suml,sumr,sum_l,sum_r;
ll a[1000100],b[1000100];
int n,T;
int main()
{
ios::sync_with_stdio(false);
srand(time(NULL));
eng.seed(rand()^time(NULL));
cin>>T;
for(int ww=1;ww<=T;ww++)//T组测试数据
{
suml=0,sumr=0;
for(int w=1;w<=n;w++)//清空
{
a[w]=0;
}
cin>>n;
for(int ww=1;ww<=n;ww++)//输入
{
cin>>a[ww];
b[ww]=a[ww];
if(ww<=n/2)//分组
{
suml+=a[ww];
}
else
{
sumr+=a[ww];
}
}
if(n==1)
{
cout<<a[1]<<"\n";
continue;
}
sum_l=suml,sum_r=sumr;
ll rec,tmp,best;
rec=abs(suml-sumr);
int cnt_=0;
best=1e18;
for(int ww=1;ww<=350;ww++)//跑350次模拟退火来实现更高的正确率
{
for(int ee=1;ee<=n;ee++)//还原状态
{
a[ee]=b[ee];
}
double Ts_=Ts;
suml=sum_l,sumr=sum_r;
while (Ts_>T0)
{
int dl=rnd(1,n/2);//随机一个临近状态，这里是随机交换两项
int dr=rnd((n/2)+1,n);
ll tl=suml;
ll tr=sumr;
tl-=a[dl],tl+=a[dr];//算新状态的答案
tr+=a[dl],tr-=a[dr];
tmp=abs(tl-tr);
double delt=rec-tmp;
if(tmp<rec)//更优则直接接受
{
rec=tmp;
suml=tl,sumr=tr;
swap(a[dl],a[dr]);
}
else
{
double ex=double(1.0*rand())/RAND_MAX;
if(exp(delt/Ts_)<ex)//否则以一定概率接受
{
rec=tmp;
suml=tl,sumr=tr;
swap(a[dl],a[dr]);
}
}
best=min(best,rec);
Ts_*=cool_;
}
}
cout<<best<<"\n";
}
return 0;
}
在这道题中使用了一个技巧：进行多次模拟退火来提高正确率
之后想到了再写吧
