二分图全面学习笔记

二分图全面学习笔记

Part1:二分图的定义与判定方法

首先，我们要知道二分图的定义是什么。

二分图的定义

​ 如果一张无向图的 \(n\) 个节点可以分成 \(A,B\) 两个不相交的非空集合，并且同一个集合之中的两个点之间没有边相连接，那么称该无向图为二分图 （Bipartite Graph）

举个栗子

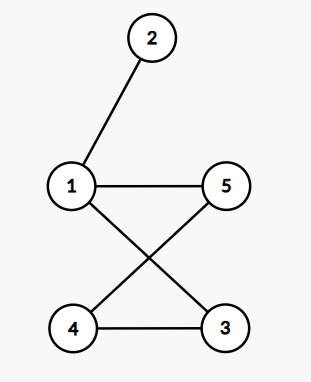
很显然的，这个图是一个二分图

那么，二分图又有什么性质呢？

二分图的性质

• 同一个集合之中的点之间没有边相连接
• 图上没有奇环
  所谓奇环，就是长度为奇数的环。显然，由于一个集合内的点之间没有直接的边相连，所以从这个点出发之后一定要经过偶数条边才能回到这个集合。所以说，二分图上没有奇环。

所以，知道了这些，我们该如何判定二分图呢？

二分图的判定方法之：染色法

我们可以用染色法来判定二分图。

即我们用两种颜色来标记图上的点，当一个点 \(i\) 被标记后，用不同的颜色标记所有与之相邻的点。这是因为所有与一个点有直接连接的点都要在另一个集合之中，所以需要染上另一种颜色。

如果有一个与 \(i\) 相邻的点和 \(i\) 染的颜色相同，即说明在这个集合内有两个点有直接的边相连，那么说明这个图不是二分图。然后将这个过程递归的进行下去，直到所有节点都被染上颜色为止。

这个过程可以用 BFS 或者 DFS 实现

代码如下

点击查看代码

#include<bits/stdc++.h>
using namespace std;
struct edge
{
	int f,t;
};
edge edges[100000];
struct node
{
	int num;
	int col;
	vector<int> to;

};
node nodes[100000];
int n,m;
int tag=1;
bool continue_tag=1;//是否有两个相同节点染上了相同颜色 
void dfs(int x)//x 表示现在在哪个节点
{
	int col=nodes[x].col;
	int to;
	for(int yy=0; yy<nodes[x].to.size(); yy++)
	{
		if(continue_tag)//如果还要继续的话 
		{
			to=edges[nodes[x].to[yy]].t;
			if(nodes[to].col==0)//如果还没有染色过 
			{
				nodes[to].col=3-col;//染上相反颜色 
				dfs(to);//递归遍历 
			}
			else//被染色过 
			{
				if(nodes[to].col==col)//如果颜色相同 
				{
					continue_tag=0;//已经不是二分图了，所以不用再继续了 
					return;
				}
			}
		}
	}
}
int main()
{
	ios::sync_with_stdio(0);
	cin>>n>>m;
	int a,b;
	for(int yy=1; yy<=m; yy++)
	{
		cin>>a>>b;
		edges[yy].f=a;
		edges[yy].t=b;
		edges[yy+m].f=b;
		edges[yy+m].t=a;
		nodes[a].to.push_back(yy);
		nodes[b].to.push_back(yy+m);
	}
	for(int ww=1; ww<=n; ww++)//防止图不连通 
	{
		if(nodes[ww].col==0)
		{
			continue_tag=1;
			dfs(ww);
			if(continue_tag==0)
			{
				tag=0;
				break; 
			}

		}
	}
	if(tag==0)
	{
		cout<<"No";
	}
	else
	{
		cout<<"Yes";
	}
	return 0;
}

判定复杂度 \(O(n+m)\)

Part2:二分图最大匹配

设 G 为二分图，若 G 的子图 M 中，任意两条边都没有公共节点，那么称 M 为二分图 G 的一组匹配。 在二分图中，包含边数最多一组匹配称为二分图的最大匹配

说人话就是,设二分图的两个集合为 \(G_1,G_2\), 两个集合之中的点互相有连边,\(G_1\) 集合中点要和 \(G_2\) 中的 与自己连了边的 点 匹配,同时,与另一个点匹配了的点不能与别的点匹配,求最大的能匹配数

再通俗一点就是:比如说有一场宴会，男孩和女孩跳舞，并且他们必须互相喜欢才能一起跳舞，一个男孩可能喜欢 \(0\) 个或多个女孩，一个女孩也可能喜欢 \(0\) 个或多个男孩，但一个男孩和他喜欢地女孩跳舞之后就不能和其他他喜欢地女孩跳舞，女孩亦是如此。请问最多可以多少对男孩女孩一起跳舞

那么,二分图的最大匹配该怎么求呢?

匈牙利算法

有一种叫匈牙利算法的算法可以在 \(O(nm)\) 的时间复杂度之内来解决这个问题

我们依次枚举 \(G_1\) 中的点 \(i\),在 \(G_2\) 中寻找他们的匹配.
我们依次遍历 在 \(G_2\) 中与 \(i\) 相连的 所有点 \(x\) ,会有两种情况

• \(x\) 还没有与别的点匹配
  直接将 \(x\) 与 \(i\) 匹配即可
• \(x\) 已经与别的点匹配了
  我们设 \(x\) 原来与 \(y\) 匹配了
  那么我们 看能否 递归的让 \(y\) 重新找到一个点匹配,
  若能,则将 \(y\) 与那个点匹配,然后将 \(x\) 与 \(i\) 匹配
  若不能,那么 \(i\) 点无法从形成匹配

形式化的理解就是原本 \(x\) 与 \(y\) 在一对 ,现在 \(y\) 还有其他舞伴 ,就把 \(x\) 让给了 \(i\)

这样就能多出一个匹配，相当于找到一条 “增广路径”

点击查看匈牙利算法的代码

#include<bits/stdc++.h>
using namespace std;
int n,m,e;
struct edge
{
	int f,t;
};
edge edges[100000];
struct node
{
	vector<int> to;
	int match;
	bool vis;
	
};
node nodes[100000];
bool dfs(int x)
{
	int to;
	for(int ww=0;ww<nodes[x].to.size();ww++)//遍历这个点的所有能够到达的点 
	{
		to=edges[nodes[x].to[ww]].t;//能到的点 
		if(nodes[to].vis)//如果要去的点被遍历过 
		{
			continue;
		}
		nodes[to].vis=1;//标记要去的点 
		if(nodes[to].match==0||dfs(nodes[to].match))//如果要去的点没被匹配 或者 与其匹配的点还有别的选择即还能和别的点匹配 
		{
			nodes[to].match=x;//这两个点匹配 
			return 1;//返回可行 
		}
	}
	return 0;//不可行 
}
int main()
{
	ios::sync_with_stdio(0);
	cin>>n>>m>>e;
	int a,b;
	for(int ww=1; ww<=e; ww++)
	{
		cin>>a>>b;
		edges[ww].f=a;
		edges[ww].t=b;
		edges[ww+e].f=b;
		edges[ww+e].t=a;
		nodes[a].to.push_back(ww);
		nodes[b+n].to.push_back(ww+e);
	}
	int ans=0;
	for(int q=1;q<=n;q++)
	{
		for(int yy=1;yy<=m;yy++)
		{
			nodes[yy].vis=0;
		}
		if(dfs(q))
		{
			ans++;
		}
	}
	cout<<ans;


	return 0;
}

网络流做法

前置知识点: 网络流

事实上,二分图的最大匹配问题也可以转化为网络流来解决

我们假设有一个超级源点,将这个点向 \(G_1\) 中的每一个点 连一条 流量 为 \(1\) 的边,\(G_1,G_2\)之间的边的流量也为 \(1\) 然后 建立一个 超级汇点 将 \(G_2\) 中的每一个点 与超级汇点建立一条 流量 为 \(1\) 的边,二分图最大匹配的问题就被转化为了网络流的最大流问题

同时,这种做法能更好的处理一些匹配问题

若跑 EK 算法 时间复杂度 \(O(n m^2)\)
若跑 Dinic 算法 时间复杂度 \(O(\sqrt{n}m)\) ,非常优秀~

Part3:补充

二分图还有一点别的东西,比如:

二分图最小点覆盖

最小点覆盖就是要选最少的点，满足二分图的每条边至少有一个端点被选。

那么,先说结论: 最小点覆盖所需点数=最大匹配的边数

点击查看证明

将二分图点集分成左右两个集合，使得所有边的两个端点都不在一个集合。

考虑如下构造：从左侧未匹配的节点出发，按照匈牙利算法中增广路的方式走，即先走一条未匹配边，再走一条匹配边。由于已经求出了最大匹配，所以这样的「增广路」一定以匹配边结束，即增广路是不完整的。在所有经过这样「增广路」的节点上打标记。则最后构造的集合是：所有左侧未打标记的节点和所有右侧打了标记的节点。

首先，这个集合的大小等于最大匹配。左边未打标记的点都一定对应着一个匹配边（否则会以这个点为起点开始标记），右边打了标记的节点一定在一条不完整的增广路上，也会对应一个匹配边。假设存在一条匹配边左侧标记了，右侧没标记，左边的点只能是通过另一条匹配边走过来，此时左边的点有两条匹配边，不符合最大匹配的规定；假设存在一条匹配边左侧没标记，右侧标记了，那就会从右边的点沿着这条匹配边走过来，从而左侧也有标记。因此，每一条匹配的边两侧一定都有标记（在不完整的增广路上）或都没有标记，匹配边的两个节点中必然有一个被选中。

其次，这个集合是一个点覆盖。由于我们的构造方式是：所有左侧未打标记的节点和所有右侧打了标记的节点。假设存在左侧打标记且右侧没打标记的边，对于匹配边，上一段已经说明其不存在，对于非匹配边，右端点一定会由这条非匹配边经过，从而被打上标记。因此，这样的构造能够覆盖所有边。

同时，不存在更小的点覆盖。为了覆盖最大匹配的所有边，至少要有最大匹配边数的点数。

证明方式来自 OIwiki

二分图:二分图最大独立集

二分图最大独立集就是要求选最多的点，满足两两之间没有边相连。

结论:因为在最小点覆盖中，任意一条边都被至少选了一个顶点，所以对于其点集的补集，任意一条边都被至多选了一个顶点，所以不存在边连接两个点集中的点，且该点集最大。因此二分图中，\(最大独立集 = n- 最小点覆盖\)。

---

完结撒花!