二分图 by LFRED2023
本文由 LFRED2023 撰写，由本人帮忙代发
二分图
二分图的定义
二分图又叫二部图，是图论的一种特殊模型
假设 $ S=(V,E) $ 是一个无向图。如果顶点 $ V $ 可分割为两个互不相交的子集 $ (A,B) $ ，并且图中的每条边 $ (i,j) $ 所关联的两个顶点 $ i $ 和 $ j $ 分别属于这两个不同的顶点集 $ (i $ $ in $ $ A $ $ ,j $ $ in $ $ B) $ ，就可以称图 $ S $ 为一个二分图。简单来说，就是顶点集 $ V $ 可分割为两个互不相交的子集,并且图中每条边依附的两个顶点都分属于这两个互不相交的子集，两个子集内的顶点不相邻。
二分图的性质
1.只要两个点之间有边，两个点就不能同属一个集合，必须分在两边。
2.二分图中不存在边数为奇数的环
二分图的判定——染色法
从一个结点出发，进行染色，每经过一条边就换成相反的颜色进行染色；
如果找到了已经被染色的结点，那么进行判定：
若和要染的颜色符合，那么继续染色；
若和要染的颜色不符合，那么判定不是二分图。
代码实现
#include<iostream>
#include<vector>
#include<cstring>
using namespace std;
const int maxn = 10010;
int n,m;//顶点数 边数
vector<int> G[maxn];
int color[maxn] ;
//0 没染色 1 -1不同色
bool dfs(int u, int c){
color[u] = c;
for(int i=0; i<G[u].size(); i++){
int v = G[u][i];
if(color[v] == c) return false;
if(color[v] == 0 && !dfs(v,-c)) return false;
}
return true;
}
bool solve(){
for(int i=1; i<=n; i++){
if(color[i] == 0)
if(!dfs(i,1)){
return false;
}
}
return true;
}
int main(){
int t;
cin>>t;
while(t--){
cin >> n >> m;
memset(color, 0, sizeof(color));
for(int i=0; i<maxn; i++) G[i].clear();
for(int i = 0; i < m; i++)
{
int s, t;
cin >> s >> t;
G[s].push_back(t);
G[t].push_back(s); // 如果有向图则无需这一句
}
if(solve()){
cout<<"Correct"<<endl;
}
else cout<<"Wrong"<<endl;
}
return 0;
}
二分图的(最大)匹配
定义
在一个无向图中，定义一条边覆盖的点为这条边的两个端点。
找到一个边集 $ S $ 包含最多的边，使得这个边集覆盖到的所有顶点中的每个顶点只被一条边覆盖。 $ S $ 的大小叫做图的最大匹配。
通俗地讲，比如说有一场宴会，男孩和女孩跳舞，并且他们必须互相喜欢才能一起跳舞，一个男孩可能喜欢 $ 0 $ 个或多个女孩，一个女孩也可能喜欢 $ 0 $ 个或多个男孩，但一个男孩和他喜欢地女孩跳舞之后就不能和其他他喜欢地女孩跳舞，女孩亦是如此。请问最多可以多少对男孩女孩一起跳舞。
很显然，互相喜欢的男孩和女孩建边得到一个二分图，求一个边集 $ S $ 包含最多的边，使得这个边集覆盖到的所有顶点中的每个顶点只被一条边覆盖。即求二分图的最大匹配。
二分图最大匹配算法——匈牙利算法
把二分图分为 $ A,B $ 两个集合，依次枚举 $ A $ 中的每个点，试图在 $ B $ 集合中找到一个匹配。
对于 $ A $ 集合中一点 $ x $ ，假设 $ B $ 中有一个与其相连的点 $ y $ ，若 $ y $ 暂时还没有匹配点，那么 $ x $ 可以和 $ y $ 匹配，找到；
否则，设 $ y $ 已经匹配的点为 $ z $ （显然 $ z $ 是 $ A $ 集合中的一个点），那么，我们将尝试为 $ z $ 找到一个除了 $ y $ 之外的匹配点，若找到，那么 $ x $ 可以和 $ y $ 匹配，否则 $ x $ 不能与 $ y $ 匹配。
算法核心
每次寻找可以匹配 $ A $ 点的一个点 $ B $ ，如果这个点 $ B $ 还没有被匹配，暂时就把这个点 $ B $ 当作 $ A $ 的匹配点；如果这个 $ B $ 在之前已经匹配了 $ C $ ，那就看 $ C $ 能不能匹配除了 $ B $ 以外的未匹配点，如果找不到则重复以上过程直到找到或者枚举所有可能点还找不到，结束点 $ A $ 的匹配；如果找到，则把 $ B $ 匀给 $ A $ （本来 $ B $ 是 $ C $ 的，现在 $ C $ 说我还有其他舞伴， $ B $ 就让给 $ A $ 了）。这样就能多出一个匹配，相当于找到一条“增广路径”。
代码实现
#include<bits/stdc++.h>
using namespace std;
int n,m,k,a,b,ans;
struct edge{
int v;
int nxt;
}e[100010];
int h[1010];
int idx;
int vis[1010];
int match[1010];
inline void add(int x,int y)
{
e[++idx].v = y;
e[idx].nxt = h[x];
h[x] = idx;
}
bool dfs(int u)
{
for(int i = h[u];i;i = e[i].nxt)
{
int v = e[i].v;
if(vis[v]) continue;
vis[v] = 1;
if(!match[v] || dfs(match[v]))
{
match[v] = u;
return 1;
}
}
return 0;
}
int main()
{
cin >> n >> m >> k;
for(int i = 1;i <= k;++i)
{
cin >> a >> b;
add(a,b + n);
}
for(int i = 1;i <= n;++i)
{
memset(vis,0,sizeof(vis));
if(dfs(i)) ans++;
}
cout << ans;
return 0;
}
二分图的应用
[洛谷P10937]車的放置
题目描述
给定一个 \(N\) 行 \(M\) 列的棋盘，已知某些格子禁止放置。
问棋盘上最多能放多少个不能互相攻击的車。
車放在格子里，攻击范围与中国象棋的“車”一致。
输入格式
第一行包含三个整数 \(N,M,T\)，其中 \(T\) 表示禁止放置的格子的数量。
接下来 \(T\) 行每行包含两个整数 \(x\) 和 \(y\)，表示位于第 \(x\) 行第 \(y\) 列的格子禁止放置，行列数从 \(1\) 开始。
保证禁止放置的格子互不相同。
输出格式
输出一个整数，表示结果。
样例 #1
样例输入 #1
8 8 0
样例输出 #1
8
提示
数据保证，\(1 \le N,M \le 200\)。
解题思路
部分分做法
当你看见这道题，你的脑海中闪过了搜索，但不大不小的数据范围打消了你美妙的幻想
但作为一个蒟蒻有什么办法呢，这就是命啊......
沦为暴力老哥
但是该说不说应该还是要一点优化的
比如可能性比较多的行先决策，可能性比较少的行后决策，这些都是常见的优化技巧
关于深搜的优化建议做一道好题洛谷P1277
正解
虽然你看不出来这是个二分图，但学新的东西就是酱子的，作为一个蒟蒻有什么办法呢......
构造一个二分图，左边结点编号 $ [1,n] $ 表示行，右边结点编号 $ [1,m] $ 表示列
对于一组匹配 $ (i,j) $ ，表示 $ (i,j) $ 的位置存在一个車
我们要求的就是二分图的最大匹配（可以自己想想为什么）
根据二分图匹配的性质，我们可以知道任意一行一列不存在两个及以上的車
二分图的最大匹配对数就是我们最多能放車的个数
代码附上（从更高级的题目里改过来的，不想再改了，凑合着看扒）
#include<bits/stdc++.h>
using namespace std;
const int N = 210;
const int M = 80010;
int to[M * 2],nxt[M * 2];
int n,m,tot = 0,n1,n2,ans,pan[N * N * 2],head[N * N * 2],match[N * N * 2],a[N][N],idh[N][N],idz[N][N];
int vis[N][N];
inline void add(int x,int y)
{
to[++tot] = y;
nxt[tot] = head[x];
head[x] = tot;
return;
}
inline int dfs(int x)
{
for(int i = head[x];i;i = nxt[i])
{
int v = to[i];
if(vis[x][v]) continue;
if(!pan[v])
{
pan[v] = 1;
if(!match[v] || dfs(match[v]))
{
match[v] = x;
return 1;
}
}
}
return 0;
}
int main()
{
// freopen("guards.in","r",stdin);
// freopen("guards.out","w",stdout);
std::ios::sync_with_stdio(false);
int t;
cin >> n >> m >> t;
string s;
for(int i = 1,x,y;i <= t;++i)
{
cin >> x >> y;
vis[x][y] = 1;
}
for(int i = 1;i <= n;++i) a[i][0] = 2;
for(int i = 1;i <= m;++i) a[0][i] = 2;
for(int i = 1;i <= n;++i)
{
for(int j = 1;j <= m;++j)
{
if(a[i][j] != 2)
{
if(a[i][j - 1] == 2) idh[i][j] = ++ n1;
else idh[i][j] = idh[i][j - 1];
}
}
}
for(int j = 1;j <= m;++j)
{
for(int i = 1;i <= n;++i)
{
if(a[i][j] != 2)
{
if(a[i - 1][j] == 2) idz[i][j] = ++n2;
else idz[i][j] = idz[i - 1][j];
}
}
}
for(int i = 1;i <= n;++i)
{
for(int j = 1;j <= m;++j)
{
if(!a[i][j]) add(idh[i][j],idz[i][j]);
}
}
for(int i = 1;i <= n1;++i)
{
for(int j = 1;j <= n2;++j) pan[j] = 0;
ans += dfs(i);
}
cout << ans << endl;
// for(int i = 1;i <= n;++i)
// {
// for(int j = 1;j <= m;++j)
// {
// if(!a[i][j] && idh[i][j] == match[idz[i][j]]) cout << i << " " << j << endl;
// }
// }
return 0;
}
[洛谷P1263] Royal guards
题目描述
从前有一个王国，这个王国的城堡是 \(m\) 行 \(n\) 列的一个矩形，被分为 \(m \times n\) 个方格。一些方格是墙，而另一些是空地。这个王国的国王在城堡里设了一些陷阱，每个陷阱占据一块空地。
一天，国王决定在城堡里布置守卫，他希望安排尽量多的守卫。
守卫们都是经过严格训练的，所以一旦他们发现同行或同列中有人的话，他们立即向那人射击。因此，国王希望能够合理地布置守卫，使他们互相之间不能看见，这样他们就不可能互相射击了。守卫们只能被布置在空地上，不能被布置在陷阱或墙上，且一块空地只能布置一个守卫。如果两个守卫在同一行或同一列，并且他们之间没有墙的话，他们就能互相看见。(守卫就像象棋里的车一样)
你的任务是写一个程序，根据给定的城堡，计算最多可布置多少个守卫，并设计出布置的方案。
输入格式
第一行有两个整数 \(m\) 和 \(n\)，表示城堡的规模。
第 \(2\) 到第 \((m + 1)\) 行，每行 \(n\) 个整数，第 \((i +1)\) 行第 \(j\) 列的数 \(a_{i, j}\) 表示城堡第 \(i\) 行第 \(j\) 列的方格的信息，其中 \(0\) 表示空地，\(1\) 表示陷阱，\(2\) 表示墙。
输出格式
本题存在 Special Judge。
首先输出一行一个整数 \(k\)，表示最多可布置的守卫个数。
然后输出 \(k\) 行，每行两个整数 \(x, y\)，表示在第 \(x\) 行第 \(j\) 列放一个守卫。
样例 #1
样例输入 #1
3 4
2 0 0 0
2 2 2 1
0 1 0 2
样例输出 #1
2
1 2
3 3
提示
样例输入输出 1 解释
如图（黑色方格为墙，白色方格为空地，圆圈为陷阱，G表示守卫）
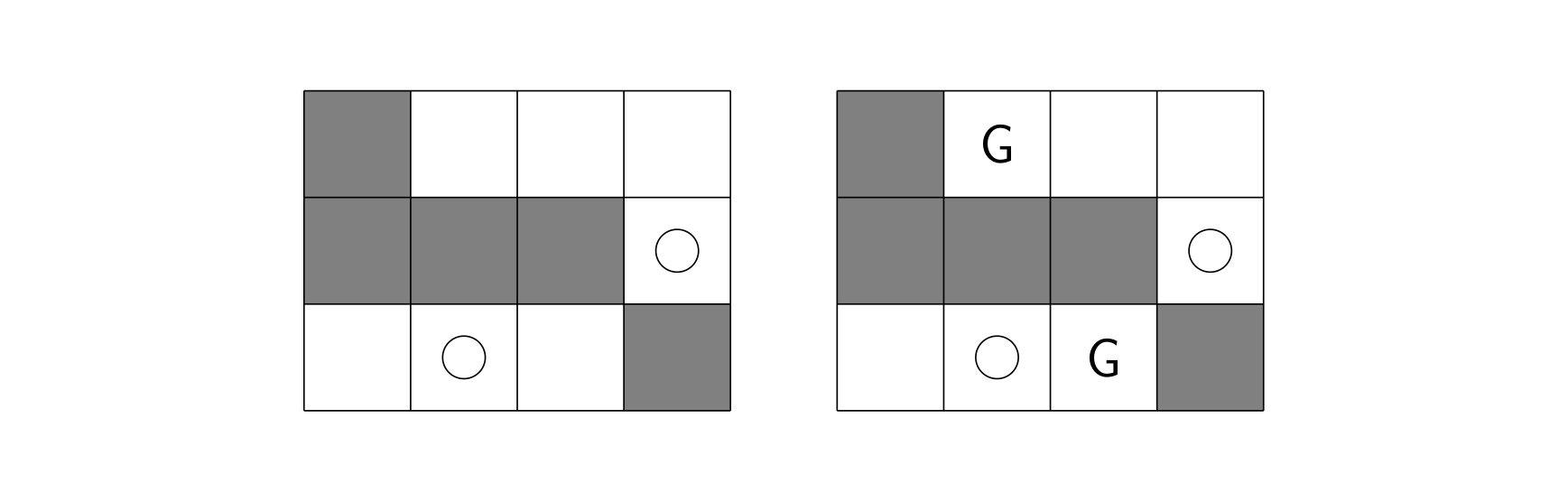
数据规模与约定
对于全部的测试点，保证 \(1 \leq m, n \leq 200\)，\(0 \leq a_{i, j} \leq 2\)。
解题思路
部分分就不用讲了扒
直接进入正解
对于一行或者一列，其中存在着若干个墙，将其分割成了几个部分，这几个部分互不干涉都可以放守卫
因此我们可以想到，对于每一个部分都建一个结点，这样就能够在一行或一列里取多个又保证答案正确性了
代码附上（这题有三倍经验，可以在洛谷讨论区获取）
#include<bits/stdc++.h>
using namespace std;
const int N = 210;
const int M = 80010;
int to[M * 2],nxt[M * 2];
int n,m,tot = 0,n1,n2,ans,pan[N * N * 2],head[N * N * 2],match[N * N * 2],a[N][N],idh[N][N],idz[N][N];
inline void add(int x,int y)
{
to[++tot] = y;
nxt[tot] = head[x];
head[x] = tot;
return;
}
inline int dfs(int x)
{
for(int i = head[x];i;i = nxt[i])
{
int v = to[i];
if(!pan[v])
{
pan[v] = 1;
if(!match[v] || dfs(match[v]))
{
match[v] = x;
return 1;
}
}
}
return 0;
}
int main()
{
// freopen("guards.in","r",stdin);
// freopen("guards.out","w",stdout);
std::ios::sync_with_stdio(false);
cin >> n >> m;
for(int i = 1;i <= n;++i)
{
for(int i1 = 1;i1 <= m;++i1)
{
cin >> a[i][i1];
}
}
for(int i = 1;i <= n;++i) a[i][0] = 2;
for(int i = 1;i <= m;++i) a[0][i] = 2;
for(int i = 1;i <= n;++i)
{
for(int j = 1;j <= m;++j)
{
if(a[i][j] != 2)
{
if(a[i][j - 1] == 2) idh[i][j] = ++ n1;
else idh[i][j] = idh[i][j - 1];
}
}
}
for(int j = 1;j <= m;++j)
{
for(int i = 1;i <= n;++i)
{
if(a[i][j] != 2)
{
if(a[i - 1][j] == 2) idz[i][j] = ++n2;
else idz[i][j] = idz[i - 1][j];
}
}
}
for(int i = 1;i <= n;++i)
{
for(int j = 1;j <= m;++j)
{
if(!a[i][j]) add(idh[i][j],idz[i][j]);
}
}
for(int i = 1;i <= n1;++i)
{
for(int j = 1;j <= n2;++j) pan[j] = 0;
ans += dfs(i);
}
cout << ans << endl;
for(int i = 1;i <= n;++i)
{
for(int j = 1;j <= m;++j)
{
if(!a[i][j] && idh[i][j] == match[idz[i][j]]) cout << i << " " << j << endl;
}
}
return 0;
}
机器调度
题目描述
我们知道机器调度是计算机科学中一个非常经典的问题。调度问题有很多种，具体条件不同，问题就不同。
现在我们要处理的是两个机器的调度问题。
有两个机器 $ A $ 和 $ B $ 。
机器 $ A $ 有 $ n $ 种工作模式，我们称之为 $ mode_0，mode_1…．，mode_n $ $ _- $ $ _1 $ 。
同样，机器 $ B $ 有 $ m $ 种工作模式，我们称之为 $ mode_0，mode_1,…，mode_m $ $ _- $ $ _1 $ 。
初始时，两台机器的工作模式均为 $ mode_0 $ 。
现在有 $ k $ 个任务，每个工作都可以在两台机器中任意一台的特定的模式下被加工。
例如， $ job_0 $ 能在机器 A 的 $ mode_3 $ 或机器 B 的 $ mode_4 $ 下被加工， $ job1 $ 能在机器 A 的 $ mode_2 $ 或机器 B 的 $ mode_4 $ 下被加工，等等。
因此，对于任意的 $ job_i $ ，我们可以用三元组 $ (i，x，y) $ 来表示 $ job_i $ 在机器 A 的 $ mode_x $ 或机器 B 的 $ mode_y $ 下被加工。
显然，要完成所有工作，我们需要不时的改变机器的工作模式。
但是，改变机器的工作状态就必须重启机器，这是需要代价的。
你的任务是，合理的分配任务给适当的机器，使机器的重启次数尽量少。
输入格式
第一行三个整数 $ n，m(n，m<100)，k(k<10000) $ 。接下来的 $ k $ 行，每行三个整数 $ i，x，y $ 。
输出格式
只一行一个整数，表示最少的重启次数。
样例 #1
样例输入 #1
5 5 10
0 1 1
1 1 2
2 1 3
3 1 4
4 2 1
5 2 2
6 2 3
7 2 4
8 3 3
9 4 3
样例输出 #1
3
数据规模与约定
30%： $ n，m<30， k<100 $
100%： $ n，m<100，k<10000 $
解题思路
对于所有 $ (x,y) $ ，我们构建一个二分图，左边是 $ x $ ，右边是 $ y $ 。
那么我们要求的答案就是这个二分图的最大匹配对数。
但作为一个蒟蒻，我不理解啊，可我有什么办法呢？
那就来愉快地证明一下吧！
假设我们已经完成了二分图的最大匹配
那么对于没有匹配的点，它所连接的点一定被其他点匹配到了，否则这就不是最大匹配
因此，这个二分图中的所有调动要求都可以被实现
证毕
代码就不用我来献丑了吧OwO
