FHQ-Treap 学习笔记(超详细)
更新日志:
2024.9.18 写完文章
2024.10.6 更正了一些细节上的错误
2024.10.10 加入了一些内容：非严格前驱/后继
2024.11.25 加入了一些例题，完善了部分内容
2024.11.26 加入可持久化相关内容
前置：了解Treap的思想和原理
FHQ-Treap 学习笔记
可以看一下 董晓算法的视频
Part 1:是什么
FHQ-Treap 又称无旋 Treap 是由 范浩强 发明的一种性能与 Splay 相当而且代码短，非常好写的平衡树
优点：功能强大，支持可持久化，可拓展性强，而且代码短，易于理解
缺点：无法用作 LCT 的辅助树，由于需要使用随机化使得性能会有一定波动
Part 1.1 前置 Treap
Treap 是一种维护二叉查找树的方式
他要求构建出来的二叉树对于键值满足二叉查找树的性质，而对于附加优先级的又要满足堆的性质
其名字 Treap 也是由 Tree 和 heap 合并而来
而为了能产生一个平衡的 BST ，这个优先级一般赋值为随机数，这样期望能生成一颗平衡的 BST
为了维护 Treap 有两种方法 第一种就是旋转法，第二种就是 FHQ 。自然，FHQ 代码更短，还能应用在更多的场合，基本可以完全取代旋转法。
Part 2 怎么实现
随机数
首先是随机数的部分，这里强力推荐使用mt19937而不是rand
mt19937 从 c++14 开始支持，不管是生成质量还是值域范围都比 rand 好了太多，而且速度和 rand 差不多
其使用如下
mt19937 xxx;//这里的xxx可以自由随意替换
srand(time(NULL));//先用time()给rand（）种子
xxx.seed(rand()^time(NULL));//再用rand()给mt19937提供种子，这样生成的随机数质量更高一些
int w=xxx();//xxx()就是生成一个随机数
变量
mt19937 rnd;
struct node
{
int l,r;//左右儿子
int val;//键值
int key;//优先级
int size;//子树大小
};
node tr[100000];
int n,root,idx;//root表示当前的根，idx表示当前的节点编号
创建节点
有两种实现方式，一种是利用上那些被删除掉的节点，第二种是直接新开节点
第一种虽然空间复杂度小，但是很容易出BUG
所以这里用第二种
int newnode(int v)
{
tr[++idx].key=rnd();
tr[idx].size=1;
tr[idx].val=v;
return idx;//返回这个新建的结点的编号
}
更新
更新以一个节点为根的子树的大小
很简单
代码如下：
void pushup(int p)
{
tr[p].size=tr[tr[p].l].size+tr[tr[p].r].size+1;
}
分裂
这是 FHQ 的核心操作之一
分裂有两种
一种是按排名分裂，还有一种是按键值分裂，
这里讲解按键值分裂
按键值分裂就是将一颗 FHQ-Treap 按某个键值 \(v\) 分裂成 \(A\) 和 \(B\)，使其满足分裂出来的 \(A\) 这一棵上的键值都小于等于 \(v\) \(B\)这一颗上的键值都大于 \(v\) ，而且分裂完之后得到的 \(A,B\) 都要满足 Treap 的性质
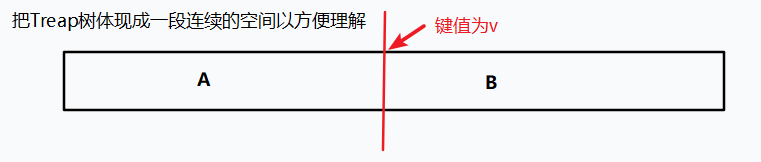
具体的函数长这样：
void split(int p,int v,int &x,int &y)
其中 \(p\) 为这一颗树的根， \(v\) 表示以 \(v\) 的键值分裂, &x 表示分裂出的 \(A\) 的根 &y表示分裂出的 \(B\) 的根
而该怎么实现这个函数呢？
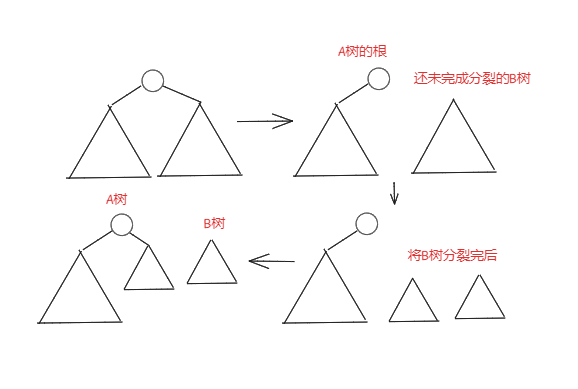
你看，如果根节点的键值都小于 \(v\) ,而左子树的键值都小于根节点，所以左子树的键值都小于 \(v\)
那么左子树一定属于分裂完之后的 \(A\)，我们只用继续分裂根节点的右子树，将右子树中键值小于 \(v\) 的节点分裂出来接在 \(A\) 的右子树上 就好了
而如果根节点的键值都大于 \(v\)，因为右子树的键值都大于 根节点的键值，所以右子树的键值都大于 \(v\)
右子树在分裂完后一定都属于 \(B\)，我们只用继续分裂根节点的左子树就好了
大致流程如图
void split(int p,int v,int &x,int &y)
{
if(!p)//如果这个节点不存在
{
x=0;
y=0;
return;
}
if(tr[p].val<=v)//如果说根节点的键值都小于等于 v 那么根节点和其的左子树一定都小于 v,所以只用递归的分裂右子树即可
{
x=p;//标记A的根
split(tr[x].r,v,tr[x].r,y);//继续分裂右子树,y还没有确定
}
else//否则就说明 右子树都大于 $v$ 所以只用递归分裂左子树即可
{
y=p;//标记B的根
split(tr[y].l,v,x,tr[y].l);//递归分裂左子树,x还没有确定
}
pushup(p); //更新本结点
}
这样子分裂出来的 \(A\), \(B\) 都满足 FHQ-Treap 的性质
所以,分裂有什么用呢?别急,我们等会就知道了
复杂度:因为期望子树是均匀的,所以每次大小都会 \(/2\)
所以是 \(O(log n)\) 级别的
按排名分裂也是类似的，就是将键值换为排名即可
合并
这是 FHQ 的另一个重要的操作
函数长这样
int merge(int x,int y)
表示将以 \(x\) 为根的 FHQ 和以 \(y\) 为根的 FHQ 合并成一颗 FHQ ,并在这个过程之中维护 FHQ 的形态
这里有个前提要求
即 \(A\) 上的所有节点的键值都要小于 \(B\) 上的所有节点的键值
所以不能随意更换 merge() 函数中的 x,y 顺序,要保证其键值满足要求
而具体的函数长这样
int merge(int x,int y)
{
if(!x||!y)//如果 x ,y之中有一个为空
{
return x+y;//直接返回另一个
}
//如果 A 的根的优先级小于 B 的根的优先级，则A的根节点为合并后的根(为了满足小根堆的性质)
if(tr[x].key<tr[y].key)
{
//这里为了保证满足BST的性质,A的左子树的键值都比A的根的键值小不用再管,需要继续维护的是A的右子树和B这棵树
tr[x].r=merge(tr[x].r,y);
pushup(x);//更新x
return x;
}
else//如果B的根的优先级小于A的根的优先级，则B的根节点为合并后的根(为了满足小根堆的性质)
{
//这里为了保证满足BST的性质,B的右子树的键值都比B的键值大不用再管,需要继续维护的是A这棵树和B的左子树
tr[y].l=merge(x,tr[y].l);
pushup(y);
return y;
}
}
复杂度:因为期望子树是均匀的,所以每次大小都会 \(/2\)
所以是 \(O(log n)\) 级别的
功能实现
实现了这些基本的函数,接下来就可以让我们去实现那些平衡树所应有的功能了
插入节点
很简单:先按要插入的键值 \(v\) 将这颗平衡树分裂为 \(A,B\) 两个部分,然后新建一个节点,将这个节点和 \(A\) 合并,将合并的产物继续与 \(B\) 合并,这不就把一个节点插入进去了吗!
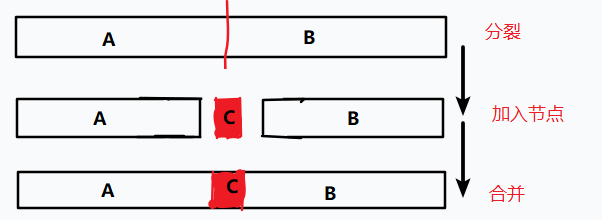
代码实现如下
void insert(int v)
{
int x,y,z;
split(root,v,x,y);//拆开
z=newnode(v);//新建节点
root=merge(merge(x,z)/*合并左树和新节点*/,y);//最后合并右树
}
删除节点
有两种删除的操作,一个是按键值删除,而还有一个是按排名删除,这里先讲按键值分裂.
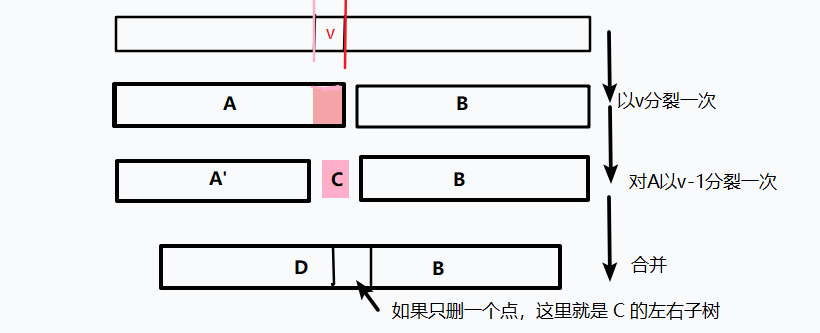
这个比较好做,比如要删除 \(v\) ,我们就先把一整棵树按 \(v\) 分裂成 \(A,B\) ,然后再把分裂出来的 \(A\) 再按 \(v-1\) 分裂
这样就把一棵树分成了三个部分 \(A',C,B\)
其中 \(A'\) 就是 键值都小于 \(v\) 的部分,而 \(C\) 是键值 等于 \(v\) 的部分, \(B\) 是键值大于 \(v\) 的部分。
如果是一次删除一个结点的话，就将 \(C\) 的左子树和右子树合并成 \(D\) ，然后把 \(D\) 依次和 \(A'，C\) 合并。
如果一次删完所有这个键值的结点的话，就直接将 \(A'\) 和 \(C\) 合并即可
流程如下图
void del(int v)
{
int x,y,z;//左中右三个部分
split(root,v,x,z);//先按v分裂一次
split(x,v-1,x,y);//再按v-1分裂一次,分离出键值等于v的节点
y=merge(tr[y].l,tr[y].r);//这里只删除一个节点,将其的左右子树合并
root=merge(merge(x,y),z);//继续合并
}
获取排名
就是获取一个键值 \(x\) 的排名。
这里给出一种方法
在每个节点上维护一个 size 表示以这个节点为根的子树大小
把树按 \(x-1\) 分裂成 A 和 B，A中包含了所有小于 \(x\) 的键值，所以 \(x\) 的排名就是 A 的大小 +1
在得到排名之后将 A 和 B 合并回去
int get_rank(int v)
{
int x,y;
split(root,v-1,x,y);
int kk=tr[x].size+1;
root=merge(x,y);
return kk;
}
求第 \(k\) 大
在这颗BST上二分寻找即可
int get_k(int p,int k)//注意,返回的是节点编号!
{
if(k<=tr[tr[p].l].size)//在左子树上
{
return get_k(tr[p].l,k);
}
if(k==tr[tr[p].l].size+1)//如果这个排名刚好是根
{
return p;
}
return get_k(tr[p].r,k-tr[tr[p].l].size-1);//在右子树上
}
获取前驱
获取元素 \(x\) 的前驱
这里有两种获取前驱
一种是非严格的前驱，就是找到第一个小于等于 自己的数
还有一种是严格前驱，就是找到第一个小于自己的数
获取严格前驱
我们将原树按 \(x-1\) 分裂成 \(A,B\) ,要求的前驱就是 \(A\) 中最大的数
这里直接用上面写好的 求第k大 函数就可以了
最后把 \(A,B\) 合并回去
int get_pre(int v)//注意,返回的是编号
{
int x,y;
split(root,v-1,x,y);//分裂
int p=get_k(x,tr[x].size);//获得 A 中最大的数
root=merge(x,y);//合并回去
return p;
}
获取非严格前驱
直接对着代码解释好了
int get_pre(int v)//注意，返回的是编号
{
int x, y, z;
splite(root, v - 1, x, y);
splite(y, v, y, z);
//将所有 键值等于 v 的节点都分离出来
if (tr[y].size > 1)//如果有大于两个，则直接返回
{
root = merge(merge(x, y), z);
return y;
}
else//否则正常获取前驱
{
int p = get_k(x, tr[x].size);
root = merge(merge(x, y), z);
return p;
}
}
还有一种常数更小的在平衡树上二分的做法
读者可以自己想一下
获取后继
和获取前驱一样,有严格和非严格两种
获取严格后继
获取元素 \(x\) 的后继
将原树按 \(x\) 分裂,得到 \(A,B\) 我们要求的后继就是 \(B\) 中的最小的元素
这里也是直接使用上面写好的 求第k大 函数
int get_suc(int v)//注意,返回的是编号
{
int x,y;
split(root,v,x,y);//分裂
int p=get_k(y,1);//获取 B 中的最小元素
root=merge(x,y);//合并回去
return p;
}
获取非严格后继
和获取非严格前驱类似
int get_suc(int v)//注意返回的是编号
{
int x, y, z;
splite(root, v, x, y);
splite(x, v - 1, x, z);
if (tr[z].size > 1)
{
root = merge(merge(x, z), y);
return z;
}
else
{
int p = get_k(y, 1);
root = merge(merge(x, z), y);
return p;
}
}
同样有常数更小的二分做法
获取第\(k\)大元素的键值
直接获取这棵树的第 \(k\) 大即可
int get_val(int k)
{
int p=get_k(root,k);
return tr[p].val;
}
总的代码
没有注释的代码点这里
#include<bits/stdc++.h>
using namespace std;
mt19937 rnd;
struct node
{
int l,r;
int val;
int key;
int size;
};
node tr[100000];
int n,root,idx;
int newnode(int v)
{
tr[++idx].key=rnd();
tr[idx].size=1;
tr[idx].val=v;
return idx;
}
void pushup(int p)
{
tr[p].size=tr[tr[p].l].size+tr[tr[p].r].size+1;
}
void split(int p,int v,int &x,int &y)
{
if(!p)
{
x=0;
y=0;
return;
}
if(tr[p].val<=v)
{
x=p;
split(tr[x].r,v,tr[x].r,y);
}
else
{
y=p;
split(tr[y].l,v,x,tr[y].l);
}
pushup(p);
}
int merge(int x,int y)
{
if(!x||!y)
{
return x+y;
}
if(tr[x].key<tr[y].key)
{
tr[x].r=merge(tr[x].r,y);
pushup(x);
return x;
}
else
{
tr[y].l=merge(x,tr[y].l);
pushup(y);
return y;
}
}
void insert(int v)
{
int x,y,z;
split(root,v,x,y);
z=newnode(v);
root=merge(merge(x,z),y);
}
void del(int v)
{
int x,y,z;
split(root,v,x,z);
split(x,v-1,x,y);
y=merge(tr[y].l,tr[y].r);
root=merge(merge(x,y),z);
}
int get_k(int p,int k)
{
if(k<=tr[tr[p].l].size)
{
return get_k(tr[p].l,k);
}
if(k==tr[tr[p].l].size+1)
{
return p;
}
return get_k(tr[p].r,k-tr[tr[p].l].size-1);
}
int get_pre(int v)
{
int x,y;
split(root,v-1,x,y);
int p=get_k(x,tr[x].size);
root=merge(x,y);
return p;
}
int get_suc(int v)
{
int x,y;
split(root,v,x,y);
int p=get_k(y,1);
root=merge(x,y);
return p;
}
int get_rank(int v)
{
int x,y;
split(root,v-1,x,y);
int kk=tr[x].size+1;
root=merge(x,y);
return kk;
}
int get_val(int k)
{
int p=get_k(root,k);
return tr[p].val;
}
int main()
{
ios::sync_with_stdio(0);
srand(time(NULL));
rnd.seed(rand()^time(NULL));
cin>>n;
int op,v;
for(int ww=1;ww<=n;ww++)
{
cin>>op>>v;
if(op==1)
{
insert(v);
}
else if(op==2)
{
del(v);
}
else if(op==3)
{
cout<<get_rank(v)<<"\n";
}
else if(op==4)
{
cout<<get_val(v)<<"\n";
}
else if(op==5)
{
cout<<tr[get_pre(v)].val<<"\n";
}
else
{
cout<<tr[get_suc(v)].val<<"\n";
}
}
return 0;
}
有注释的版本点这里
#include<bits/stdc++.h>
using namespace std;
mt19937 rnd;
struct node
{
int l,r;//左右儿子
int val;//键值
int key;//优先级
int size;//子树大小
};
node tr[100000];
int n,root,idx;//root表示当前的根，idx表示当前的节点编号
int newnode(int v)
{
tr[++idx].key=rnd();
tr[idx].size=1;
tr[idx].val=v;
return idx;//返回这个新建的结点的编号
}
void pushup(int p)
{
tr[p].size=tr[tr[p].l].size+tr[tr[p].r].size+1;
}
void split(int p,int v,int &x,int &y)
{
if(!p)//如果这个节点不存在
{
x=0;
y=0;
return;
}
if(tr[p].val<=v)//如果说根节点的键值都小于等于 v 那么根节点和其的左子树一定都小于 v,所以只用递归的分裂右子树即可
{
x=p;//标记A的根
split(tr[x].r,v,tr[x].r,y);//继续分裂右子树,y还没有确定
}
else//否则就说明 右子树都大于 $v$ 所以只用递归分裂左子树即可
{
y=p;//标记B的根
split(tr[y].l,v,x,tr[y].l);//递归分裂左子树,x还没有确定
}
pushup(p); //更新本结点
}
int merge(int x,int y)
{
if(!x||!y)//如果 x ,y之中有一个为空
{
return x+y;//直接返回另一个
}
//如果 A 的根的优先级小于 B 的根的优先级，则A的根节点为合并后的根(为了满足小根堆的性质)
if(tr[x].key<tr[y].key)
{
//这里为了保证满足BST的性质,A的左子树的键值都比A的根的键值小不用再管,需要继续维护的是A的右子树和B这棵树
tr[x].r=merge(tr[x].r,y);
pushup(x);//更新x
return x;
}
else//如果B的根的优先级小于A的根的优先级，则B的根节点为合并后的根(为了满足小根堆的性质)
{
//这里为了保证满足BST的性质,B的右子树的键值都比B的键值大不用再管,需要继续维护的是A这棵树和B的左子树
tr[y].l=merge(x,tr[y].l);
pushup(y);
return y;
}
}
void insert(int v)
{
int x,y,z;
split(root,v,x,y);//拆开
z=newnode(v);//新建节点
root=merge(merge(x,z)/*合并左树和新节点*/,y);//最后合并右树
}
void del(int v)
{
int x,y,z;//左中右三个部分
split(root,v,x,z);//先按v分裂一次
split(x,v-1,x,y);//再按v-1分裂一次,分离出键值等于v的节点
y=merge(tr[y].l,tr[y].r);//这里只删除一个节点,将其的左右子树合并
root=merge(merge(x,y),z);//继续合并
}
int get_k(int p,int k)//注意,返回的是节点编号!
{
if(k<=tr[tr[p].l].size)//在左子树上
{
return get_k(tr[p].l,k);
}
if(k==tr[tr[p].l].size+1)//如果这个排名刚好是根
{
return p;
}
return get_k(tr[p].r,k-tr[tr[p].l].size-1);//在右子树上
}
int get_pre(int v)//注意,返回的是编号
{
int x,y;
split(root,v-1,x,y);//分裂
int p=get_k(x,tr[x].size);//获得 A 中最大的数
root=merge(x,y);//合并回去
return p;
}
int get_suc(int v)//注意,返回的是编号
{
int x,y;
split(root,v,x,y);//分裂
int p=get_k(y,1);//获取 B 中的最小元素
root=merge(x,y);//合并回去
return p;
}
int get_rank(int v)
{
int x,y;
split(root,v-1,x,y);
int kk=tr[x].size+1;
root=merge(x,y);
return kk;
}
int get_val(int k)
{
int p=get_k(root,k);
return tr[p].val;
}
int main()
{
ios::sync_with_stdio(0);
srand(time(NULL));
rnd.seed(rand()^time(NULL));
cin>>n;
int op,v;
for(int ww=1;ww<=n;ww++)
{
cin>>op>>v;
if(op==1)
{
insert(v);
}
else if(op==2)
{
del(v);
}
else if(op==3)
{
cout<<get_rank(v)<<"\n";
}
else if(op==4)
{
cout<<get_val(v)<<"\n";
}
else if(op==5)
{
cout<<tr[get_pre(v)].val<<"\n";
}
else
{
cout<<tr[get_suc(v)].val<<"\n";
}
}
return 0;
}
例题
模板，不需要讲
这题正解不一定要用平衡树
但是也可以用平衡树加上莫队来直接胡过去
这是用平衡树来维护一个序列的例子
事实上，平衡树还有一个很强大的功能就是维护序列的翻转。
平衡树也能像线段树一样维护懒标记，所以理论上也许可以实现线段树的一些功能？
这是一个很典的 trick
就是我们将一个元素在序列中的位置来当成这个元素的大小进行排名，然后就可以借助懒标记实现区间翻转
具体的，我们对于平衡树上的每一个节点来维护一个翻转标记，表示这个区间是否被反转
下传标记就是交换这个节点的两个子树，然后将子树的标记取反
然后就可以做了
就是上一题的加了别的操作
对于每个节点，我们维护一下这个子树的值的最小值
每次操作我们在平衡树上二分找到最小值的位置也就是排名
然后用按排名分裂来将这个子树分裂出去，打上翻转标记并删去这个最小值即可
但是有些细节要注意一下
可持久化平衡树
FHQ 有一个优点就是可以实现可持久化
至于如何实现？
就像可持久化线段树一样
在对树进行操作时复制一份新版本，在新版本上操做
具体来说就是进行分裂和合并时复制节点，
插入和删除都会产生新的版本
对于每个版本记录一下根节点即可
别的操做没什么区别
放一下有变化的部分的代码
点击查看代码
void splite(int p, int v, int &x, int &y)
{
if (!p)
{
x = 0;
y = 0;
return;
}
if (tr[p].val <= v)
{
x = newnode();//复制新节点
tr[x] = tr[p];
splite(tr[x].r, v, tr[x].r, y);
update(x);
}
else
{
y = newnode();
tr[y] = tr[p];
splite(tr[y].l, v, x, tr[y].l);
update(y);
}
}
int merge(int x, int y)
{
if (!x || !y)
{
return x + y;
}
if (tr[x].key < tr[y].key)
{
int rt = newnode();//复制节点
tr[rt] = tr[x];
tr[rt].r = merge(tr[rt].r, y);
update(rt);
return rt;//返回这个新版本
}
else
{
int rt = newnode();//同上
tr[rt] = tr[y];
tr[rt].l = merge(x, tr[rt].l);
update(rt);
return rt;
}
}
int insert(int rt, int v)
{
int x, y, z = newnode(v);
splite(rt, v, x, y);
int nrt = merge(merge(x, z), y);
return nrt;//返回新版本
}
int del(int rt, int v)
{
int x, y, z;
splite(rt, v, x, z);
splite(x, v - 1, x, y);
y = merge(tr[y].l, tr[y].r);
int nrt = merge(merge(x, y), z);
return nrt;
}
