乘法逆元(费马小定理+扩欧)学习笔记
数学之乘法逆元
Part1 : 逆元是什么
一个东西 的逆元，就是指在一种运算/操作下能够抵消这个东西对单位元所带来影响的东东
举个例子 4 的加法逆元 就是 -4
2 在普通乘法中的逆元就是 \(2^{-1}\)
而乘法逆元指的是在 模意义 下的乘法逆元
设原式为
\(1*a \equiv a \mod p\)
那么 \(a\) 的乘法逆元乘上去之后的效果就是
这里的 \(a^{-1}\) 指的是 \(a\) 的乘法逆元
\(1*a*a^{-1} \equiv 1 \mod p\)
即：
\(a*a^{-1} \equiv 1 \mod p\)
ps:知道了这些，以下的所有内容中的 \(xxx^{-1}\) 表示 \(xxx\) 的乘法逆元
Part2 ：有什么用
举个例子 要求出 $ \frac{a}{b} mod \ p$ 的值 ， 那该怎么算呢？
我们要知道的是，在模意义下，除以一个数等于乘以一个数的逆元
所以 \(\frac{a}{b} \bmod \ p =a*b^{-1} \bmod \ p\)
Part3 : 该怎么求
所以乘法逆元到底要怎么求呢？
有三种求法
Part3.1: 费马小定理
当 \(p\) 是质数时
\(a^{p-1} \equiv 1 \mod p\)
所以
\(a*a^{p-2} \equiv 1 \mod p\)
那么
\(a^{p-2}\)就是 \(a\) 在模 \(p\) 意义下的乘法逆元
这个可以用快速幂实现
Part3.2：扩展欧几里得算法
当 \(p\) 不是质数时，就要用到扩展欧几里得算法了
那么要学会扩欧，先要学会 欧几里得定理 这个东西
欧几里得定理（辗转相除法）
\(gcd(a,b)=gcd(b,a\%b)\)
我不会证
知道了这个，我们继续讲讲扩欧
扩展欧几里得定理
我们有 \(a\) , \(b\)
现在要求出满足 \(ax + by =gcd(a,b)\) 的最小的 \(x\) 和其对应的 \(y\)
假如我们之前求出来了一组数 \(x_2,y_2\) 使得 \(bx_2 + (a \bmod b)y_2 = gcd(a,b)\)
那么 \(ax + by =bx_2 + (a \bmod b)y_2\) （3）
那当这个假如成立时怎么求呢？
取模运算的本质其实是 \(a \bmod b = a - b×\left \lfloor \frac{a}{b} \right \rfloor\)
所以 \(3\) 式本质上是
\(ax + by =bx_2 + (a - b×\left \lfloor \frac{a}{b} \right \rfloor)*y_2\) 继续推
\(ax + by =ay_2+bx_2 - b*\left \lfloor \frac{a}{b} \right \rfloor*y_2\)
\(ax + by =ay_2+b(x_2 - \left \lfloor \frac{a}{b} \right \rfloor*y_2)\)
那么，\(x,y\) 必然有一组解为 \(x=y_2,y=(x_2 - \left \lfloor \frac{a}{b} \right \rfloor*y_2)\)
所以，我们只用求出 \(x_2,y_2\) 就可以得出 \(x,y\) 了
那么，\(x_2,y_2\) 该怎么求呢？
我们手上的要求的式子变为了
\(bx_2 + (a\bmod b)y_2 = gcd(a,b)\)
然后不断重复上面的求解过程，解出 \(x_2,y_2\)，但又要解出 \(x_3,y_3\)
这个过程中 \(x,y\) 的系数 \(s_x,s_y\) 不断被替换为 \(s_y,s_x\%s_y\)
直到最后，一定会出现 \(s_n=gcd(a,b),s_n=0\)
这个时候
方程长这样 \(s_xx_n+s_yy_n=gcd(a,b)\)
很明显的，当 \(x_n=1\) 时上式一定成立，这个时候 \(y_n\) 取任意值都可以，但建议取 0 免得神奇错误
然后不断回溯
直到回到第一层，就可以求解出 \(x_1,y_1\) 了
但是还有一点点问题，我们现在求出的 \(x_1,y_1\) 只是一组特解，\(x_1\) 可以很大，很小甚至是负数
这个问题要怎么解决呢？
那就是将 \(x\) 批量的 加上/减去 \(b\)
这是因为
\(ax+by=1\)
\(ax+by+k*b*a-k*b*a=1\)
\(a(x+k*b)+b(y-k*a)=1\)
可见 \(x+k*b,y-k*a\) 也是方程的一组解
如果我们想要得出最小的正整数解的话，
这里的 批量的 加上/减去 \(b\) 就可以看作是对 \(b\) 取模
所以我们只用这么加上一行代码
x = (x % b + b) % b;//括号中取模再加，可以处理负数
代码如下
x = (x % b + b) % b;//括号中取模再加，可以处理负数
exgcd 的 代码如下：
pair<int, int> exgcd(int a, int b)
{
if (b == 0)
{
return {1, 0};
}
int x_2, y_2; //新的解
int x, y; //这一层的解
pair<int, int> get_num = exgcd(b, (a % b));
x_2 = get_num.first;
y_2 = get_num.second;
x = y_2;
y = (x_2 - (a / b) * y_2);
return {x, y};
}
好，你知道了这个，那么就可以继续了
我们先令 \(x=a^{-1}\)
所以
\(ax \equiv 1 \mod b\)
对于这个同余方程，我们将其变一下形式
\(ax + by = 1\) （4）
其中 \(y\) 为一负数
哎，这不跟我们先前推的 扩展欧几里得 的式子特别特别像吗
那我们对 \(4\) 式做一下操作是不是就可以变成一个形式呢？
但是这里的 \(1\) 和 \(gcd(a,b)\) 又有什么关系？
是这样的： \(ax+by=k\) 有解的必要条件是 \(k \bmod gcd(a,b) =0\)
这是因为 \(a\) 为 \(gcd(a,b)\) 的倍数，那么 \(ax\) 也是 \(gcd(a,b)\) 的倍数
同理，\(by\) 也是 \(gcd(a,b)\) 的倍数， \(ax+by\) 自然也是 \(gcd(a,b)\) 的倍数
即 \(k \bmod gcd(a,b) =0\)
那现在对于 \(4\) 式来说, \(k\) 等于 \(1\)
那么 \(1 \bmod gcd(a,b) = 0\)
这说明 \(gcd(a,b)\) 就是 \(1\) 啊！
所以，我们可以得出，
若方程有解，则 \(a,b\) 一定互质
即 \(a,b\) 互质时，我们这个方程解出来（如果有的话）的 \(x\) 就是 \(a\) 在模 \(b\) 意义下的逆元
求逆元的问题就被我们解决了！
再放一遍代码
#include <bits/stdc++.h>
using namespace std;
pair<int, int> exgcd(int a, int b)
{
if (b == 0)
{
return {1, 0};
}
int x_2, y_2; //新的解
int x, y; //这一层的解
pair<int, int> get_num = exgcd(b, (a % b));
x_2 = get_num.first;
y_2 = get_num.second;
x = y_2;
y = (x_2 - (a / b) * y_2);
return {x, y};
}
int main()
{
ios::sync_with_stdio(false);
int a, b;
cin >> a >> b;
pair<int, int> x_y = exgcd(a, b);
x_y.first = (x_y.first % b + b) % b;//括号中取模再加，可以处理负数
cout << x_y.first;
return 0;
}
复杂度最劣为 \(O(\log min(a,b))\)
Part3.3递推做法
搬自 OIwiki
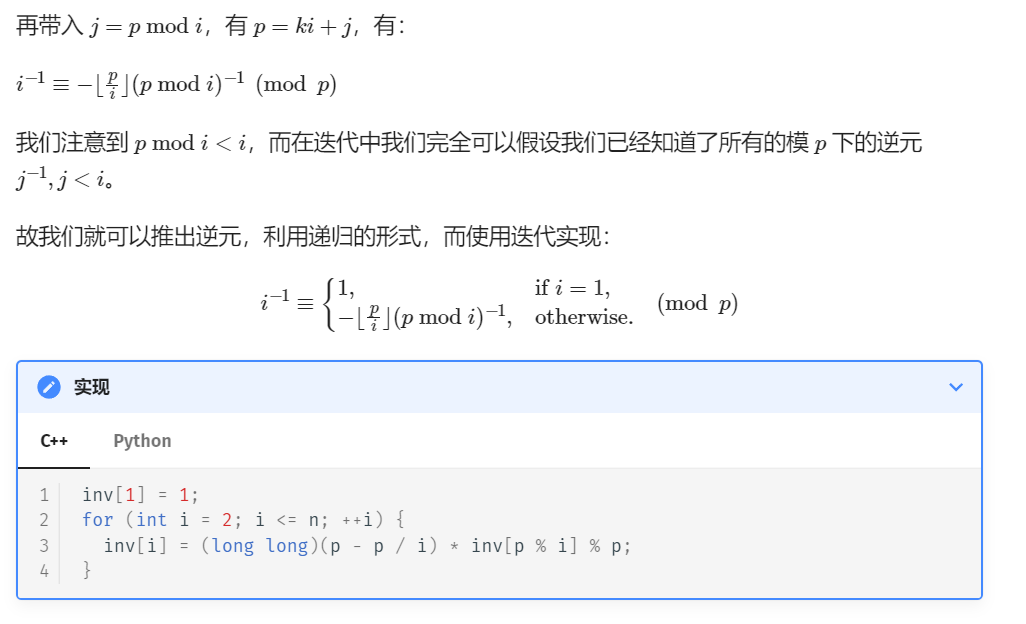
预计在 8.28 将其变成自己的理解
未完待续
