Tarjan 之 割点 学习笔记

首先，要求割点，我们需要知道割点是什么

割点： 是指在无向连通图中，如果删除某个顶点后，图的连通分量增加，则称该顶点为割点

好，知道了这个，那我们怎么去求他呢？

Tarjan 大神给出了一种依然基于时间戳的算法

图片来源：董晓算法

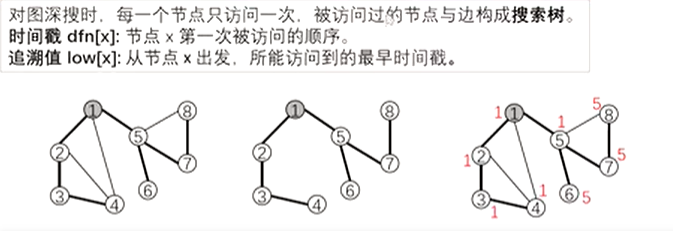
割点的求法大概就是这样的
所以细节还是见代码吧

#include<bits/stdc++.h>
using namespace std;
int n,m;
struct node
{
    vector<int > to;
    int dfn;
    int low;
    bool cut;
};
node nodes[100000];
int tot;
int root;

void tarjan(int x)
{
    nodes[x].dfn=nodes[x].low=++tot;//标记DFN值
    int chi=0;//子节点
    int to;
    for(int ww=0;ww<nodes[x].to.size();ww++)
    {
        to=nodes[x].to[ww];
        if(nodes[to].dfn==0)//如果这个儿子节点还没被访问过
        {
            tarjan(to);//递归的跑Tarjan
            nodes[x].low=min(nodes[x].low,nodes[to].low);//更新本节点的low值
            if(nodes[to].low>=nodes[x].dfn)//如果子节点的low值比本节点的DFN大
            {
                chi++;
                if(x!=root||chi>1)
                {
                    nodes[x].cut=1;//是割点
                }
            }
        }
        else//如果没被访问过
        {
            nodes[x].low=min(nodes[x].low,nodes[to].dfn);//更新low值
        }
    }
}
int main()
{
    ios::sync_with_stdio(false);
    cin>>n>>m;
    int a,b;
    for(int yy=1;yy<=m;yy++)
    {
        cin>>a>>b;
        nodes[a].to.push_back(b);
        nodes[b].to.push_back(a);
    }
    for(root=1;root<=n;root++)
    {
        if(!nodes[root].dfn)
        {
            tarjan(root);
        }
    }
    int ans=0;
    for(int ww=1;ww<=n;ww++)
    {
        ans+=nodes[ww].cut;
    }
    cout<<ans<<endl;

    for(int ww=1;ww<=n;ww++)
    {
        if(nodes[ww].cut)
        {
            cout<<ww<<" ";
        }
    }
    return 0;
}