算法学习笔记之树链剖分
算法学习笔记之（熟练跑分）树链剖分
PART 1
首先是第一部份，也就是熟练跑分最最最基础的用法 —— 求 \(LCA\)
首先是树链剖分
//图片出自 董晓算法
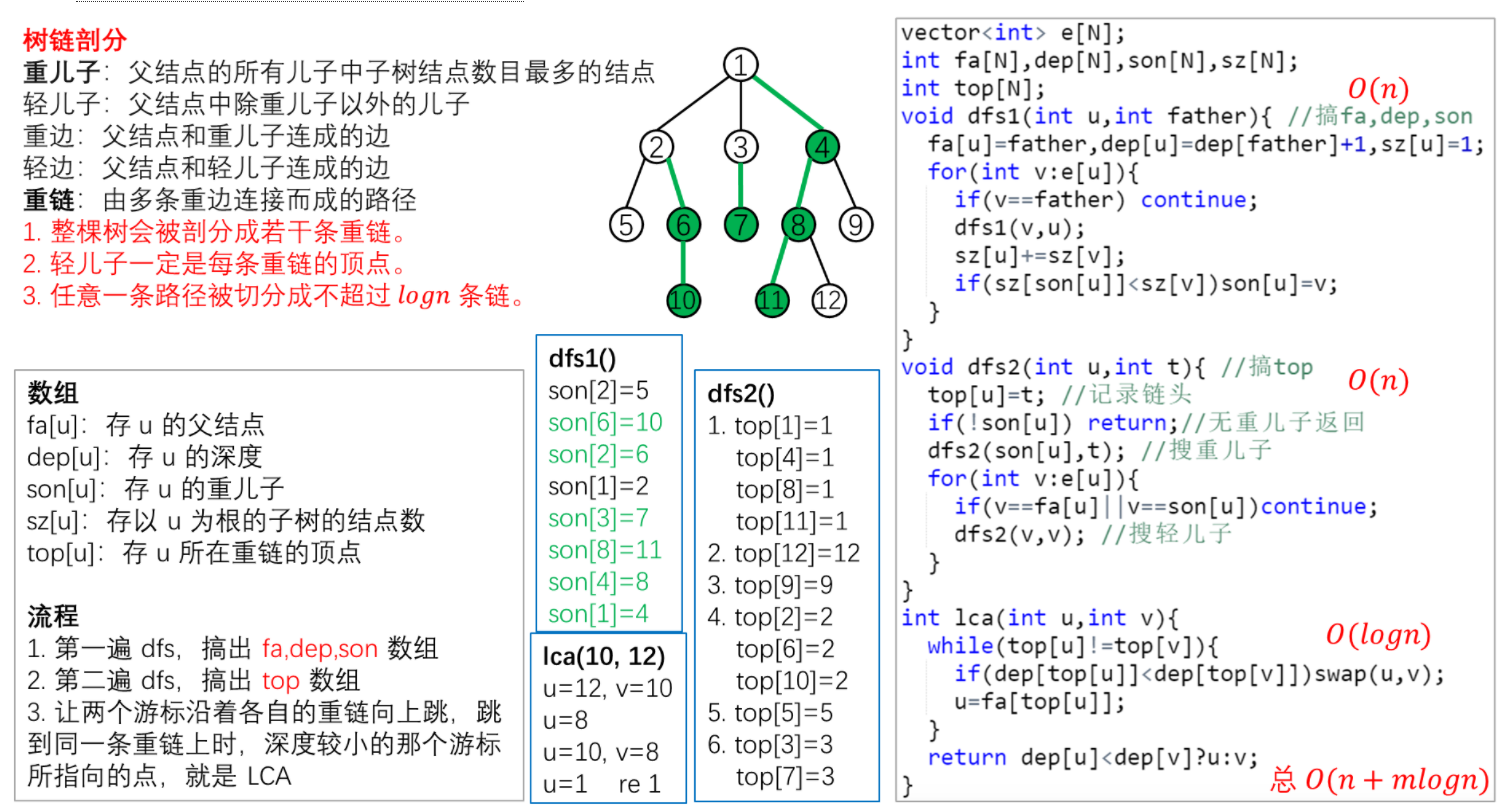
大概就是这样
本质就是根据子树大小将一颗树剖分成若干条链
然后更加方便地 处理/加速处理 信息
所以
直接
上代码？
不，还要证明树链剖分求LCA 的正确性
这个嘛
因为树剖求是不断将将链头深度大的跳，
由于链的定义，最后一定会跳到同一链上，这就是LCA
算了，不好讲，自己画一下图理解一下吧
还可以照着代码理解一下
点击查看代码
#include <bits/stdc++.h>
using namespace std;
int n, m, s;
const int min_ = -999999999;
struct node
{
vector<int> son;
int fa; //父节点
int size_; //一次节点为根的子树大小
int top; //所在链的顶端
int hson=0; //重儿子 heavy son 直接存节点编号
int deep; //此节点的深度
};
node nodes[1000000];
void build_tree(int now_) //建树，同时记录重儿子，大小和深度 相比其他模板我的版本码量稍大，但更好理解
{
nodes[now_].deep = nodes[nodes[now_].fa].deep + 1; //记录深度
nodes[now_].size_ = 1; //初始大小为一
int to_, max_ = min_, wma=0; //最大值，及其位置；
for (int yy = 0; yy < nodes[now_].son.size(); yy++)
{
to_ = nodes[now_].son[yy];
if (to_ != nodes[now_].fa)
{
nodes[to_].fa = now_; //设置儿子结点的父亲节点
build_tree(to_);
nodes[now_].size_ += nodes[to_].size_; //加上儿子结点的大小
if (nodes[to_].size_ > max_) //记录重儿子
{
max_ = nodes[to_].size_;
wma = to_;
}
}
}
nodes[now_].hson = wma;
}
void get_top(int now_, int top_) //剖分一棵树,top_为链根
{
// cout<<now_<<" getting"<<endl;
nodes[now_].top = top_; //记录本节点top
if (nodes[now_].hson == 0) //如果没有重儿子
{
return;
}
get_top(nodes[now_].hson, top_); //搜重儿子
int to_;
for (int ww = 0; ww < nodes[now_].son.size(); ww++) //搜所有子节点
{
to_ = nodes[now_].son[ww];
if (to_ != nodes[now_].fa && to_ != nodes[now_].hson) //搜所有轻儿子
{
get_top(to_, to_);
}
}
}
int get_lca(int a, int b)//求LCA
{
while (nodes[a].top != nodes[b].top)//他们还不在一条链上
{
if (nodes[nodes[a].top].deep < nodes[nodes[b].top].deep) //将链顶深度深的放在a
{
swap(a, b);
}
a = nodes[nodes[a].top].fa;//跳链
}
return nodes[a].deep < nodes[b].deep ? a : b;//返回LCA
}
int main()
{
ios::sync_with_stdio(false);
cin >> n >> m >> s;
int a, b;
for (int ww = 1; ww < n; ww++)
{
cin >> a >> b;
nodes[a].son.push_back(b);
nodes[b].son.push_back(a);
}
build_tree(s);
get_top(s, s);
for (int yy = 1; yy <= m; yy++)
{
cin >> a >> b;
cout << get_lca(a, b) << "\n";
}
return 0;
}
//例1
//求LCA
//例2
//熟练跑分基础运用
// P3384
PART 2
- 加上线段树！
- 怎么说
- 是这样的 我们在dfs求链头的时候 会有一个访问的先后顺序，不难看出，同一条重链上的编号一定是连续的
如下图
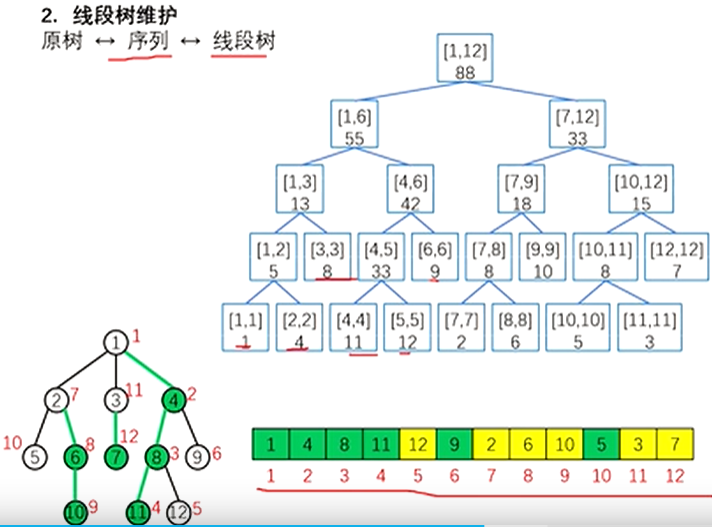
我们可以把树上所有的点按深搜到的顺序有序的映射到一个数组上，将树上的修改问题变为了数组中的区间修改/查询
然后就可以用线段树维护信息了
细节看代码(区区200行而已!)
点击查看代码
#include <bits/stdc++.h>
using namespace std;
int n, m, r;
long long p;
const long long min_ = -99999999999;
struct tree //线段树部分
{
int l, r;
long long sum;
long long tag;
};
tree t[410000];
struct node //树剖部分
{
int top;
int fa;
int hson;
long long deep;
long long size_;
vector<int> son;
};
int cnt = 0;
long long w[200000]; //旧权值
long long id[200000]; //用来存剖分后每个结点的新编号
long long nw[200000]; //新权值
node nodes[1000000];
//以下为线段树，无需多言
void update(int p)
{
t[p].sum = t[p << 1].sum + t[p << 1 | 1].sum;
}
void build(int p, int l, int r)
{
t[p].l = l;
t[p].r = r;
if (l == r)
{
t[p].sum = nw[l];
return;
}
int mid = (l + r) >> 1;
build(p << 1, l, mid);
build(p << 1 | 1, mid + 1, r);
update(p);
}
void pushdown(int p)
{
if (t[p].tag)
{
t[p << 1].sum += (t[p << 1].r - t[p << 1].l + 1) * t[p].tag;
t[p << 1].tag += t[p].tag;
t[p << 1 | 1].sum += (t[p << 1 | 1].r - t[p << 1 | 1].l + 1) * t[p].tag;
t[p << 1 | 1].tag += t[p].tag;
t[p].tag = 0;
}
}
void change(int p, int l, int r, long long delt)
{
if (l <= t[p].l && r >= t[p].r)
{
t[p].tag += delt;
t[p].sum += (t[p].r - t[p].l + 1) * delt;
return;
}
pushdown(p);
int mid = (t[p].l + t[p].r) >> 1;
if (l <= mid)
{
change(p << 1, l, r, delt);
}
if (r > mid)
{
change(p << 1 | 1, l, r, delt);
}
update(p);
return;
}
long long query(int p, int l, int r)
{
if (l <= t[p].l && r >= t[p].r)
{
return t[p].sum;
}
pushdown(p);
long long ans = 0;
int mid = (t[p].l + t[p].r) >> 1;
if (l <= mid)
{
ans += query(p << 1, l, r);
}
if (r > mid)
{
ans += query(p << 1 | 1, l, r);
}
return ans;
}
//以下为树剖正常build_tree 见PART1
void build_tree(int now_)
{
nodes[now_].deep = nodes[nodes[now_].fa].deep + 1;
nodes[now_].size_ = 1;
long long to_, max_ = min_, wma = 0;
for (int rr = 0; rr < nodes[now_].son.size(); rr++)
{
to_ = nodes[now_].son[rr];
if (to_ != nodes[now_].fa)
{
nodes[to_].fa = now_;
build_tree(to_);
nodes[now_].size_ += nodes[to_].size_;
if (nodes[to_].size_ > max_)
{
max_ = nodes[to_].size_;
wma = to_;
}
}
}
nodes[now_].hson = wma;
}
void get_top(int now, int top) //在要修改环境之下要魔改
{
nodes[now].top = top;
id[now] = ++cnt;//dfs序号
nw[id[now]] = w[now];//映射新值
if (nodes[now].hson == 0)//没有重儿子
{
return;
}
get_top(nodes[now].hson, top);
int to_;
for (int yy = 0; yy < nodes[now].son.size(); yy++)
{
to_ = nodes[now].son[yy];
if (to_ != nodes[now].fa && to_ != nodes[now].hson)
{
get_top(to_, to_);
}
}
}
long long query_path(int a, int b) //查询路径长
{
long long ans = 0;
while (nodes[a].top != nodes[b].top)//跳链
{
if (nodes[nodes[a].top].deep < nodes[nodes[b].top].deep)
{
swap(a, b);
}
ans += query(1, id[nodes[a].top], id[a]);//加上跳的这一段距离 易证这个节点所在链的链头的 dfs序 小于 这个节点的 dfs序
a = nodes[nodes[a].top].fa;
}
if (nodes[a].deep < nodes[b].deep)
{
swap(a, b);
}
ans += query(1, id[b], id[a]);//加上最后的一段距离
return ans;
}
void change_path(int a, int b, long long delt)//更改整条路经
{
while (nodes[a].top != nodes[b].top)
{
if (nodes[nodes[a].top].deep < nodes[nodes[b].top].deep)
{
swap(a, b);
}
change(1, id[nodes[a].top], id[a], delt);//更改跳的这一段 易证这个节点所在链的链头的 dfs序 小于 这个节点的 dfs序
a = nodes[nodes[a].top].fa;
}
change(1, min(id[a],id[b]), max(id[a],id[b]), delt);
}
void change_tree(int p, long long delt) //更改子树
{
change(1, id[p], id[p] + nodes[p].size_ - 1, delt);//易证一个子树的 dfs序 一定在 [根的dfs序，到根的dfs序+此树大小] 这一段
//这是因为当搜索一个子树时会把这个子树遍历完再回溯出去，一定经过了 此树大小 个节点
}
long long query_tree(int p)//查询子树
{
return query(1, id[p], id[p] + nodes[p].size_ - 1);
}
int main()
{
ios::sync_with_stdio(false);
cin >> n >> m >> r >> p;
for (int yy = 1; yy <= n; yy++)
{
cin >> w[yy];
}
int a, b, c;
long long d;
for (int yy = 1; yy < n; yy++)
{
cin >> a >> b;
nodes[a].son.push_back(b);
nodes[b].son.push_back(a);
}
build_tree(r);
get_top(r, r);
build(1, 1, n);
for (int qq = 1; qq <= m; qq++)
{
cin >> a;
if (a == 1)
{
cin >> b >> c >> d;
change_path(b, c, d);
}
if (a == 2)
{
cin >> b >> c;
cout << query_path(b, c)%p << "\n";
}
if (a == 3)
{
cin >> b >> d;
change_tree(b, d);
}
if (a == 4)
{
cin >> b;
cout << query_tree(b) %p<< "\n";
}
}
return 0;
}
PART3
有时在进行树链剖分时的权值是边权，这个时候就需要我们将边权变为点权
看似没什么问题
然而
在区间求和和区间修改时会发现，我们跑对点 \(a\) , \(b\) 之间的路径进行 查讯/修改 跑出来的值/结果 多 加上/修改 了 \(lca(a,b)\)
而点 \(a\) , \(b\) 之间的路径不会经过 \(lca(a,b)\) 上面这条边，也就不会影响到 点 \(lca(a,b)\) 对应的权值
对于这种情况，区间查询时应将 \(lca(a,b)\) 的权值删去，区间修改时不应将 \(lca(a,b)\) 的权值进行修改
总之，自己画一下图，能够更好的理解这个细节
完结散花！
