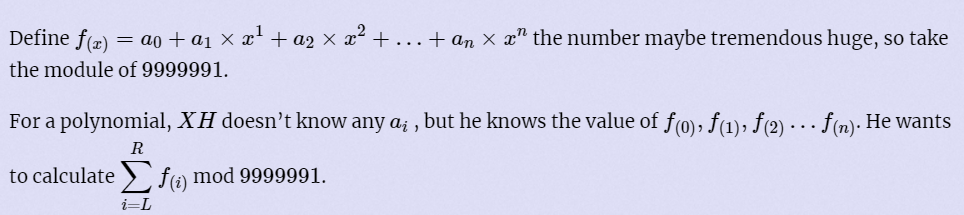【2020 12月模板】
\[Author: zhl\\
LastEdit: 2020.12.10
\]
一、杂项
1.0 导言
【ACM模板】v 3.0
基本都是这个学期学习的内容，整理完发现自己这个学期还是学了不少东西，不过也只有100天左右。
整理着也发现了自己还没有学的东西更多，希望下一个版本的 v 4.0 更充实完整
希望自己退役的时候能留下一个比较全的模板
1.1 快读
一般情况下不会卡 scanf
洛谷偷过来的一份文件流快读
class QIO {
public:
char buf[1 << 21], * p1 = buf, * p2 = buf;
inline int getc() {
return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++;
}
int read() {
int ret = 0, f = 0;
char ch = getc();
while (!isdigit(ch)) {
if (ch == '-')
f = 1;
ch = getc();
}
while (isdigit(ch)) {
ret = ret * 10 + ch - 48;
ch = getc();
}
return f ? -ret : ret;
}
char Buf[1 << 21], out[20];
int P, Size = -1;
inline void flush() {
fwrite(Buf, 1, Size + 1, stdout);
Size = -1;
}
void write(int x, char ch = ' ') {
if (Size > 1 << 20) flush();
if (x < 0) Buf[++Size] = 45, x = -x;
do {
out[++P] = x % 10 + 48;
} while (x /= 10);
do {
Buf[++Size] = out[P];
} while (--P);
Buf[++Size] = ch;
}
} io;
__int128
一般情况不会用到 read, 比较常用 print
inline __int128 read(){
__int128 x = 0, f = 1;
char ch = getchar();
while(ch < '0' || ch > '9'){
if(ch == '-')
f = -1;
ch = getchar();
}
while(ch >= '0' && ch <= '9'){
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
inline void print(__int128 x){
if(x < 0)putchar('-'), x = -x;
if(x > 9)print(x / 10);
putchar(x % 10 + '0');
}
1.2 大数
java
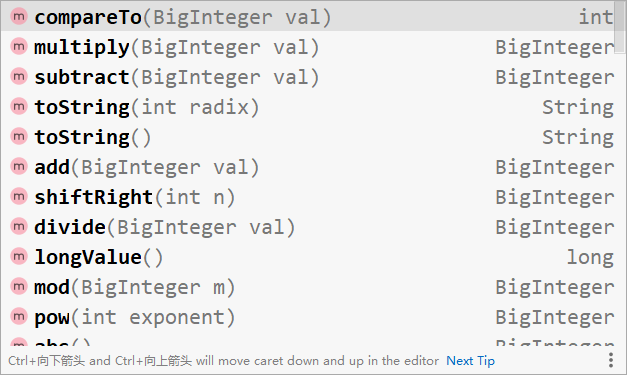
//A+B
import java.io.BufferedInputStream;
import java.math.BigInteger;
import java.util.Scanner;
public class Main{
public static void main(String[] args){
Scanner in = new Scanner(new BufferedInputStream(System.in));
BigInteger a = in.nextBigInteger();
BigInteger b = in.nextBigInteger();
// BigInteger.ONE;
// BigInteger.ZERO;
// BigInteger.TEN;
a = a.add(b);
System.out.println(a);
}
}
python
大数开根号
from math import *
from decimal import *
getcontext().prec= 300 #设置有效位数
def sqrt(n):
return floor(Decimal(n).sqrt())
def judge(n):
t = sqrt(n)
return t * t == n
1.3 模拟算法
模拟退火
- 爬山算法：兔子朝着比现在高的地方跳去。它找到了不远处的最高山峰。但是这座山不一定是珠穆朗玛峰。这就是爬山算法，它不能保证局部最优值就是全局最优值。
- 模拟退火：兔子喝醉了。它随机地跳了很长时间。这期间，它可能走向高处，也可能踏入平地。但是，它渐渐清醒了并朝最高方向跳去。这就是模拟退火。
根据热力学规律并结合计算机对离散数据的处理, 我们定义: 如果当前温度为 \(T\), 当前状态与新状态之间的能量差为 \(ΔE\), 则发生状态转移的概率为:
\[P(\Delta E) = e^{\dfrac {\Delta E} {T}}
\]
当 \(\Delta E\) 为正的时候一定是转移成功的，对于 $\Delta E < 0 $ , 则通过计算的概率接受这个新的解
可以写出如下一段伪代码
void mnth(){ //模拟退火...
for(double T = 初始温度;T > 终止温度;T *= 系数){
rand_operate();//做一个随机操作
now = cal(); //计算目前的答案
if(now < ans) ans = now;//若更优，直接转移
else if(exp((ans - now) / T) * RAND_MAX < rand()){
//这里写的是小于号，是不转移
//不转移，撤销刚刚的随机操作
}
}
}
看两道题
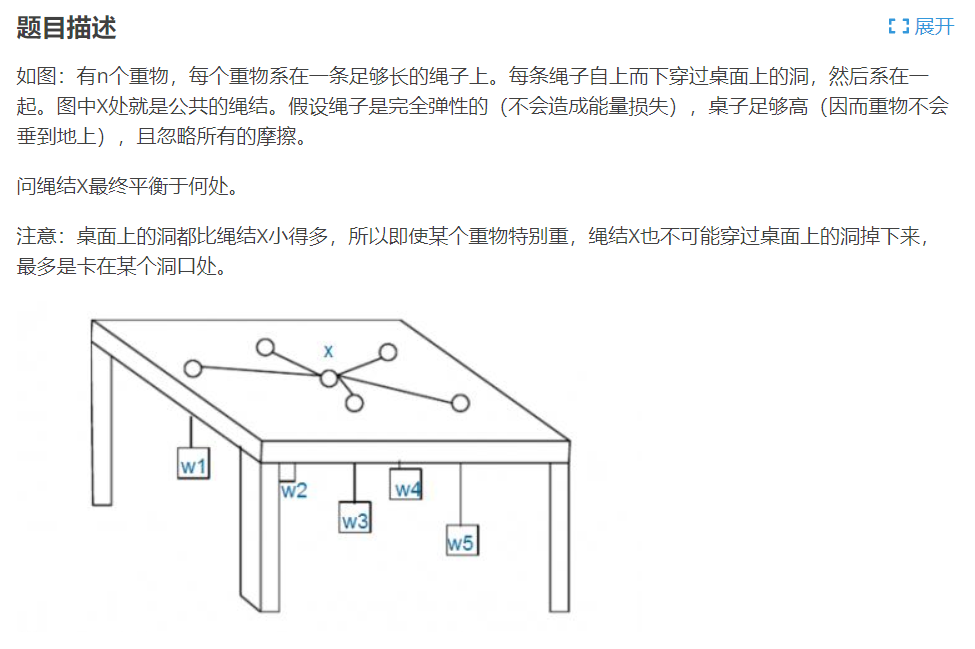
其实就是选一个点，使得这个点到所有点的距离乘上质量之和要最小
相当于在二维的平面找一个最优解
#include<bits/stdc++.h>
#define N 2000
using namespace std;
struct node
{
double x, y, w;
}e[N];
int n;
double ansx, ansy;
const double eps = 1e-15;
double f(double x, double y)
{
double tot = 0;
for (int i = 1; i <= n; i++){
double delx = x - e[i].x;
double dely = y - e[i].y;
tot += sqrt(delx * delx + dely * dely) * e[i].w;
}
return tot;
}
void mnth()
{
for(double T = 5000;T > 1e-15;T *= 0.995){
double nowx = ansx + (rand() * 2 - RAND_MAX) * T;
double nowy = ansy + (rand() * 2 - RAND_MAX) * T;
double delta = f(nowx, nowy) - f(ansx, ansy);
if (delta < 0)ansx = nowx, ansy = nowy;
else if (exp(-delta / T)> rand()*1.0/RAND_MAX)ansx = nowx, ansy = nowy;
}
}
int main(){
scanf("%d", &n);
for (int i = 1; i <= n; i++){
scanf("%lf%lf%lf", &e[i].x, &e[i].y, &e[i].w);
ansx += e[i].x; ansy += e[i].y;
}
ansx /= (double)n; ansy /= (double)n;
mnth();
printf("%.3lf %.3lf\n", ansx, ansy);
}
现在有 \(n\) 枚金币，它们可能会有不同的价值，第 \(i\) 枚金币的价值为 \(v_i\) 。
现在要把它们分成两部分，要求这两部分金币数目之差不超过 1 ，问这样分成的两部分金币的价值之差最小是多少？
每次随机交换两个元素
当时这里的小于号和大于号弄混了，调了好久
#include<bits/stdc++.h>
using namespace std;
int ans, T, n, A[50];
int get() {
int sum = 0;
for (int i = 0; i < n; i++) {
if (i < n / 2)sum += A[i];
else sum -= A[i];
}
return abs(sum);
}
void mnth() {
for (double T = 5000; T > 1e-15; T *= 0.945) {
int x = rand() % n, y = rand() % n;
swap(A[x], A[y]); int now = get();
if (now < ans) ans = now;
else if (exp((ans - now) / T) * RAND_MAX < rand()) swap(A[x], A[y]); // > 是转移， < 是撤销
}
}
int main() {
scanf("%d", &T);
while (T--) {
scanf("%d", &n);
for (int i = 0; i < n; i++)scanf("%d", A + i);
ans = 0x7fffffff; int x = 1000; while (x--)mnth();
printf("%d\n", ans);
}
}
[P4035 [JSOI2008\]球形空间产生器 - 洛谷 ](https://www.luogu.com.cn/problem/P4035)
题意：
给 \(n\) 维球体上的 \(n+1\) 个点，确定圆心坐标
/*
* @Author: zhl
* @Date: 2020-01-21 17:30:34
*/
#include<bits/stdc++.h>
using namespace std;
double p[30][30], ans[30], mx, now[30];
int n;
double sqr(double x) {
return x * x;
}
double cal(double* ar) {
double mx = 0;
double r = 0;
for (int i = 1; i <= n; i++) {
r += sqr(p[0][i] - ar[i]);
}
for (int i = 1; i <= n; i++) {
double x = 0;
for (int j = 1; j <= n; j++) {
x += sqr(p[i][j] - ar[j]);
}
mx += sqr(x - r);
}
return mx;
}
int main() {
scanf("%d", &n);
for (int i = 0; i <= n; i++) {
for (int j = 1; j <= n; j++) {
scanf("%lf", &p[i][j]);
}
}
mx = 1e18;
for (double T = 5000; T > 1e-18; T *= 0.99995) {
for (int i = 1; i <= n; i++) {
now[i] = ans[i] + (rand() * 2 - RAND_MAX) * T;
}
double delta = cal(now) - cal(ans);
if (delta < 0) {
for (int i = 1; i <= n; i++)ans[i] = now[i];
}
else if (exp(-delta / T) > rand() * 1.0 / RAND_MAX) {
for (int i = 1; i <= n; i++)ans[i] = now[i];
}
}
for (int i = 1; i <= n; i++) {
printf("%.3f ", ans[i]);
}
}
爬山算法
1.4 分数规划
1.5 杂项
线性预处理
/*
* @Author: zhl
* @Date: 2020-10-12 21:04:36
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int fac[N],invfac[N],inv[N];
const int mod = 998244353;
void init(){
fac[0] = invfac[0] = 1;
fac[1] = invfac[1] = 1;
inv[1] = 1;
for(int i = 2;i < N;i++){
fac[i] = fac[i-1] * i % mod;
inv[i] = (mod - mod / i)*inv[mod % i] % mod;
invfac[i] = invfac[i-1] * inv[i] % mod;
}
}
int C(int n,int m){
return fac[n]*invfac[n-m] % mod *invfac[m] % mod;
}
约瑟夫环
求 n 个人玩，间隔 k， 第 m 个出圈的人
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const ll mod = 1e9 + 7;
const int N = 1000;
ll cal1(ll n, ll m, ll k) {
ll p = m % (n - k + 1);
if (p == 0) p = n - k + 1;
for (ll i = 2; i <= k; i++) {
p = (p + m - 1) % (n - k + i) + 1;
}
return p;
}
ll cal2(ll n, ll m, ll k) {
if (m == 1) return k;
else {
ll a = n - k + 1, b = 1;
ll c = m % a, x = 0;
if (c == 0) c = a;
while (b + x <= k) {
a += x, b += x, c += m * x;
c %= a;
if (c == 0) c = a;
x = (a - c) / (m - 1) + 1;
}
c += (k - b) * m;
c %= n;
if (c == 0) c = n;
return c;
}
}
ll n, m, k, ans;
int main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int t;
cin >> t;
for (int i = 1; i <= t; i++) {
cin >> n >> m >> k;
if (m < k)ans = cal1(n, k, m);
else ans = cal2(n, k, m);
cout << "Case #" << i << ": " << ans << endl;
}
return 0;
}
三元环计数
三元环计数
无向图三元环计数
将无向图转化成有向图，度大的指向度小的，若度一样，按照编号排序。
枚举每个点x，将x的所有相邻点标记，然后枚举x的相邻点y，再枚举y的相邻点z，
如果z已经被标记，那么(x,y,z)就是如图示的三元环。
复杂度 : \(O(m\sqrt m)\)
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i = a;i <= b;i++)
#define repE(i,u) for(int i = head[u];i;i = E[i].next)
int n, m;
const int N = 1e5 + 10;
const int M = 2e5 + 10;
struct Edge {
int to, next;
}E[M];
int head[N], tot;
void addEdge(int from, int to) {
E[++tot] = Edge{ to,head[from] };
head[from] = tot;
}
int deg[N], s[M], t[M];
int vis[N];
int main() {
scanf("%d%d", &n, &m);
for (int i = 0; i < m; i++) {
scanf("%d%d", s + i, t + i); deg[s[i]]++; deg[t[i]]++;
}
for (int i = 0; i < m; i++) {
int u = s[i], v = t[i];
if (deg[u] == deg[v] and u < v)swap(u, v);
if (deg[u] < deg[v])swap(u, v);
addEdge(u, v);
}
int ans = 0;
rep(u, 1, n) {
repE(i, u) vis[E[i].to] = u;
repE(i, u) {
int to = E[i].to;
repE(j, to) {
int v = E[j].to;
if (vis[v] == u) {
ans++;
}
}
}
}
printf("%d\n", ans);
}
1.6 注意
memset
memset 是按字节初始化， memset(dis,0x7fffffff,sizeof dis) 这种写法是错误的，实际上只会取最低的一个字节 0xff ， 所以相当于全部置成 0xffffffff ,就是 -1
第二个参数的值应该是 0-255 （0x00 - 0xff)
priority_queue
默认是大顶堆，每次取最大的值，可以用 greater<> 变成小顶堆
二、基础算法
我不会
三、搜索
我也不会
四、字符串
4.1 KMP
\(O(n)\) 的字符串匹配
nxt数组
nxt 数组是对于匹配串 p 来说的
nxt[i] 表示 p.substr(0,i) 不包括自己 的最长公共前缀后缀
| A | C | A | B | ||
|---|---|---|---|---|---|
| -1 | 0 | 0 | 0 | 1 | 2 |
/*
* @Author: zhl
* @LastEditTime: 2020-12-07 10:09:32
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 2e6 + 10;
char s[N], p[N];
int nxt[N], n, m, ans[N], cnt;
void get_nxt() {
nxt[0] = -1;
for (int k = -1, j = 0; j < m;) {
if (k == -1 or p[k] == p[j])nxt[++j] = ++k;
else k = nxt[k];
}
}
void kmp() {
for (int j = 0, i = 0; i < n;) {
if (j == -1 or p[j] == s[i]) {
i++, j++;
if (j == m)j = nxt[j], ans[++cnt] = i - m;
}
else j = nxt[j];
}
}
int main() {
scanf("%s", s); n = strlen(s);
scanf("%s", p); m = strlen(p);
get_nxt();
kmp();
for (int i = 1; i <= cnt; i++)printf("%d\n", ans[i] + 1);
for (int i = 1; i <= m; i++)printf("%d%s", nxt[i], i == m ? "\n" : " ");
}
最小循环节
字符串 \(p\) 的最小循环节的长度为 \(m - nxt[m]\)
4.2 Manacher
\(O(n)\) 复杂度求解最长回文子串
/*
* @Author: zhl
* @LastEditTime: 2020-12-07 10:50:16
*/
class Solution {
public:
string longestPalindrome(string s) {
int n = s.length();
if (n < 2)return s;
string t = "$";
for (int i = 0;i < n;i++) {
t += "#" + s[i];
}
t += "#@";
n = t.length();
vector<int>p;p.resize(n + 10);
int id = 0, mx = 0;int maxlen = 0, cen = 0;
for (int i = 1;i < n - 1;i++) {
p[i] = i < mx ? min(mx - i, p[2 * id - i]) : 1;
while (t[i - p[i]] == t[i + p[i]])p[i]++;
if (i + p[i] > mx) {
mx = i + p[i];
id = i;
}
if (p[i] - 1 > maxlen) {
maxlen = p[i] - 1;
cen = i;
}
}
int st = (cen - maxlen) / 2;
return s.substr(st, maxlen);
}
};
4.3 Ac自动机
多模式匹配，根据多模式串建立 Tire 树， 然后建立 Fail 指针， Fail 指针指的是最长后缀
/*
* @Author: zhl
* @Date: 2020-10-14 11:36:01
*/
#include<bits/stdc++.h>
using namespace std;
// 求模式串出现了多少个，所以每个串只能访问一次
const int N = 6e6 + 10;
queue<int>q;
struct {
int c[N][26], fail[N], val[N], cnt;
int newnode() {
++cnt;
for (int i = 0; i < 26; i++)c[cnt][i] = 0;
fail[cnt] = 0;
return cnt;
}
void init() {
cnt = 0;
for (int i = 0; i < 26; i++)c[0][i] = 0;
fail[0] = 0;
}
void insert(char* s) {
int len = strlen(s); int now = 0;
for (int i = 0; i < len; i++) {
int v = s[i] - 'a';
if (!c[now][v])c[now][v] = newnode();
now = c[now][v];
}
val[now]++;
}
void getFail() {
for (int i = 0; i < 26; i++) {
if (c[0][i])fail[c[0][i]] = 0, q.push(c[0][i]);
}
while (!q.empty()) {
int u = q.front(); q.pop();
for (int i = 0; i < 26; i++) {
if (c[u][i]) {
fail[c[u][i]] = c[fail[u]][i];
q.push(c[u][i]);
}
else c[u][i] = c[fail[u]][i];
}
}
}
int query(char* s) {
int len = strlen(s); int now = 0, ans = 0;
for (int i = 0; i < len; i++) {
now = c[now][s[i] - 'a'];
for (int t = now; t && val[t] != -1; t = fail[t]) {
ans += val[t];
val[t] = -1;
}
}
return ans;
}
}Ac;
int n;
char p[N];
int main() {
scanf("%d", &n);
Ac.init();
for (int i = 1; i <= n; i++) {
scanf("%s", p);
Ac.insert(p);
}
Ac.getFail();
scanf("%s", p);
printf("%d\n", Ac.query(p));
}
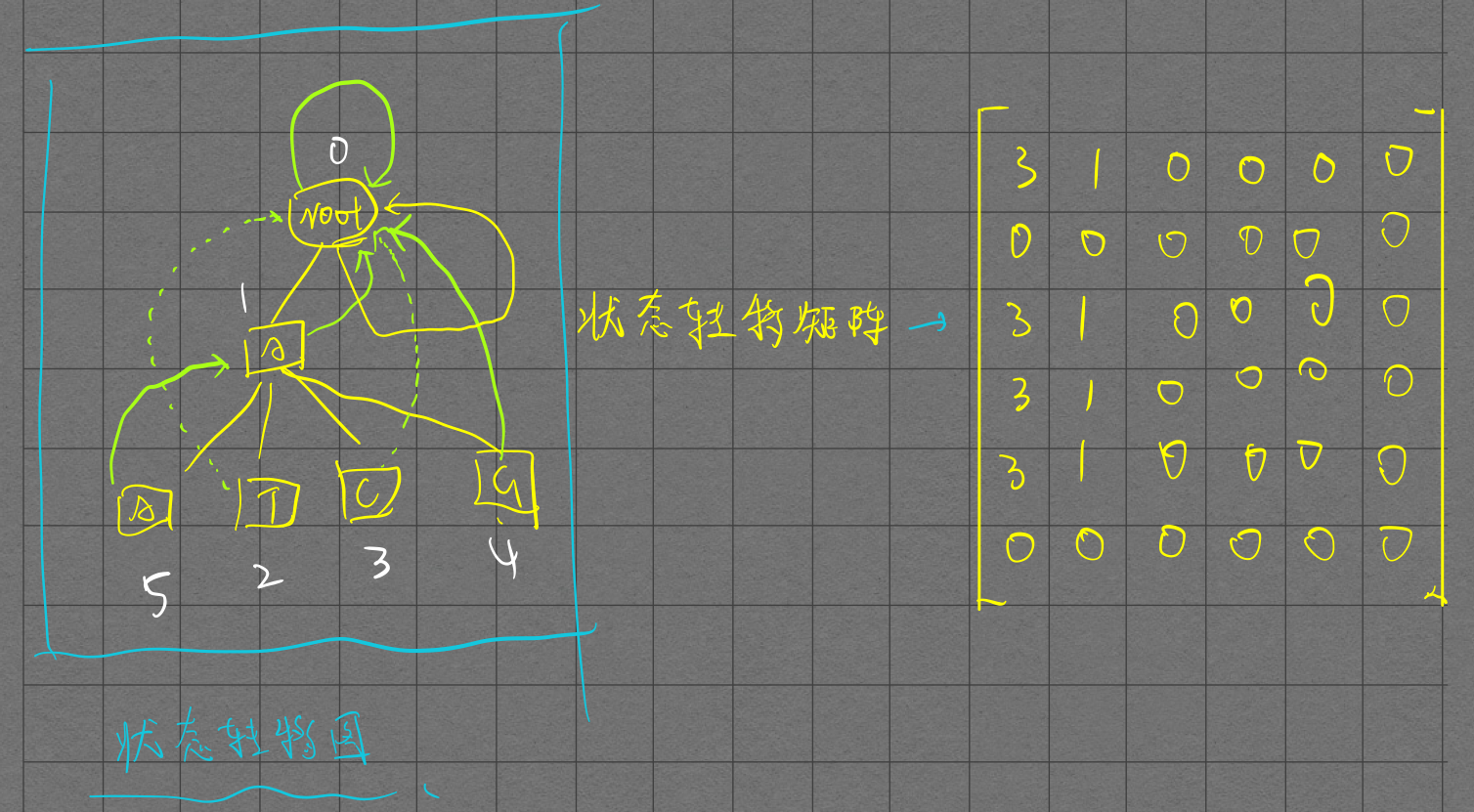
AC自动机经常和状态转移的题目有关，可以做状态转移矩阵加矩阵快速幂计数。也可以结合状态转移进行高斯消元解方程。
其实Ac自动机的Tire树就是一个状态转移图，构造出状态转移矩阵， \(M_{ij}\) 表示从Tire树上的第 \(i\) 个节点转移到 \(j\) 节点的方案数， \(M^n\) 就是长度为 \(n\) 的串的状态转移矩阵， \(M_{0i}\) 表示从根节点转移到 \(i\) 经过 \(n\) 次的方案数，\(ans= \sum_iM_{0i}\)
在处理Tire树的时候要稍微注意一些小的细节。
主要就是标记的传递
if(val[fail[u]]) val[u] = 1
以输入：
4 3 AT AC AG AA为例
#include<cstdio>
#include<map>
#include<cstring>
#include<queue>
#include<string>
#define int long long
using namespace std;
const int N = 5e5 + 10;
queue<int>q;
const int mod = 1e5;
map<char, int>id;
struct Mat {
int m[100][100], n;
Mat(int _n, int v) {
n = _n;
memset(m, 0, sizeof m);
for (int i = 0; i < n; i++)m[i][i] = v;
}
Mat operator *(const Mat& b)const {
Mat res = Mat(b.n, 0);
int n = b.n;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) {
res.m[i][j] = (res.m[i][j] + m[i][k] * b.m[k][j]) % mod;
}
}
}
return res;
}
};
struct {
int c[N][4], fail[N], val[N], cnt;
void insert(char* s) {
int len = strlen(s); int now = 0;
for (int i = 0; i < len; i++) {
int v = id[s[i]];
if (!c[now][v])c[now][v] = ++cnt;
now = c[now][v];
}
val[now]++;//这里写++好像过不去
//val[now] = 1;
}
void clear() {
memset(c, 0, sizeof c);
memset(val, 0, sizeof val);
cnt = 0;
memset(fail, 0, sizeof fail);
}
void getFail() {
for (int i = 0; i < 4; i++) {
if (c[0][i])fail[c[0][i]] = 0, q.push(c[0][i]);
}
while (!q.empty()) {
int u = q.front(); q.pop();
//***
if (val[fail[u]] == 1) {
val[u] = 1;
}
for (int i = 0; i < 4; i++) {
if (c[u][i]) {
fail[c[u][i]] = c[fail[u]][i];
q.push(c[u][i]);
}
else c[u][i] = c[fail[u]][i];
}
}
}
int query(char* s) {
int len = strlen(s); int now = 0, ans = 0;
for (int i = 0; i < len; i++) {
now = c[now][id[s[i]]];
for (int t = now; t && val[t] != -1; t = fail[t]) {
ans += val[t];
val[t] = -1;
}
}
return ans;
}
Mat getMat() {
//这里是cnt + 1
Mat res = Mat(cnt + 1, 0);
for (int i = 0; i <= cnt; i++) {
for (int j = 0; j < 4; j++) {
if (!val[c[i][j]]) {
res.m[i][c[i][j]]++;
}
}
}
return res;
}
}Ac;
Mat qpow(Mat a, int p) {
Mat res = Mat(a.n, 1);
while (p) {
if (p & 1) res = a * res;
a = a * a;
p >>= 1;
}
return res;
}
int n;
char p[N];
signed main() {
char s[] = "ACGT";
for (int i = 0; i < 4; i++)id[s[i]] = i;
int n, m, x;
while (~scanf("%lld%lld", &m, &n)) {
Ac.clear();
for (int i = 0; i < m; i++) {
scanf("%s", p);
Ac.insert(p);
}
Ac.getFail();
Mat mat = Ac.getMat();
mat = qpow(mat, n);
int ans = 0;
for (int i = 0; i < mat.n; i++) {
ans = (ans + mat.m[0][i]) % mod;
}
printf("%lld\n", ans);
}
}
4.4 后缀数组
后缀数组可以求出一个串 \(s\) 的所有后缀的排名
有两种算法
倍增 ： \(O(nlogn)\) 常数小
DC3 ： \(O(n)\) 常数大
这里使用倍增就可以
在 \(O(nlogn)\) 的时间求出以下信息
sa 数组， sa[i] 表示排第 i 位的是第 sa[i] 个后缀
rk 数组， rk[i] 表示第 i 个后缀的排名是 rk[i]
height[i] 表示第 sa[i] 个后缀与 sa[i-1] 的最长公共前缀
如何倍增
首先把所有后缀按照第一个字母排序，使用 \(O(n)\) 的基数排序
假设已经按前 \(k\) 个字母排好序，下轮考虑前 \(2k\) 个字母
我们把前 \(k\) 个字母看作第一关键字， 后 \(k\) 个字母看作第二关键字
则只需要按照第二关键字排好序，然后再按第一关键字进行稳定的基数排序，就可以完成按照前 \(2k\) 个字母排序
我们发现，第 \(i\) 个后缀的第二关键字是第 \(i + k\) 个后缀的第一关键字
void get_sa() {
//先按照第一个字母排序
for (int i = 1; i <= n; i++) c[x[i] = s[i]] ++;
for (int i = 2; i <= m; i++) c[i] += c[i - 1]; //小于等于i的数目
for (int i = n; i; i--) sa[c[x[i]] --] = i;
//开始倍增
for (int k = 1; k <= n; k <<= 1){
int num = 0;
for (int i = n - k + 1; i <= n; i++) y[++num] = i; //第二关键字是空串，肯定在最前面
for (int i = 1; i <= n; i++)
if (sa[i] > k)
y[++num] = sa[i] - k;
for (int i = 1; i <= m; i++) c[i] = 0;
for (int i = 1; i <= n; i++) c[x[i]] ++;
for (int i = 2; i <= m; i++) c[i] += c[i - 1];
//按第二关键字倒序枚举
for (int i = n; i; i--) sa[c[x[y[i]]] --] = y[i], y[i] = 0;
swap(x, y); //把 x 暂时存到 y 中
//离散化
x[sa[1]] = 1, num = 1;
for (int i = 2; i <= n; i++)
x[sa[i]] = (y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k]) ? num : ++num;
if (num == n) break;
m = num;
}
}
如何求 height 数组
首先定义
\(lcp(i,j)\) 表示排名为 \(i\) 的后缀和排名为 \(j\) 的后缀的最长公共前缀长度
则显然有一下几条性质
- \(lcp(i,j) = lcp(j,i)\)
- \(lcp(i,i) = len(i)\)
还有一条如下的性质, 对于 $ i \le k \le j$
\[lcp(i,j) = min\bigg\{lcp(i,k),lcp(k,j)\bigg\}
\]
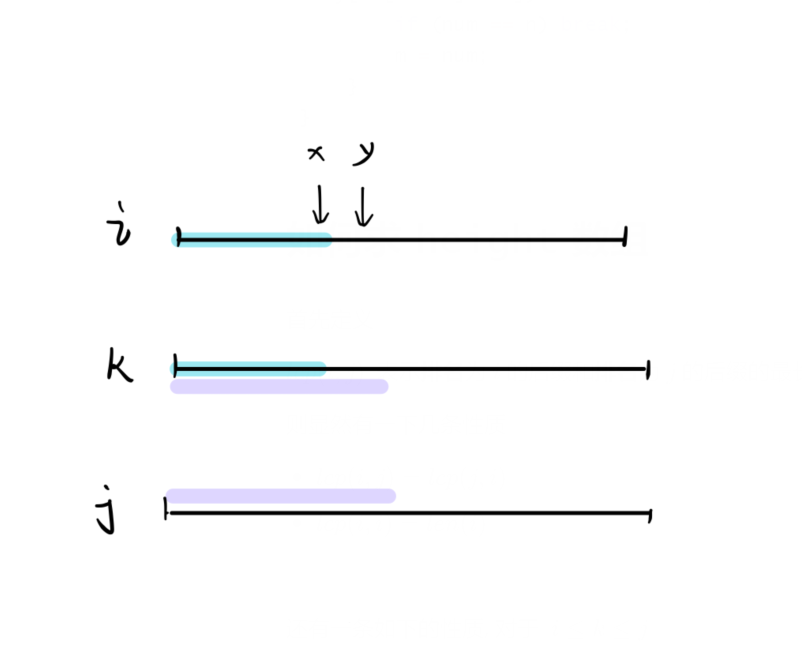
\(i\) 和 \(j\) 在 \(y\) 处的字符不会相等，若相等则 \(lcp(i,k)\) 可以继续扩展
由此可以推出
\[lcp(i,j) = min\bigg\{ lcp(i,i+1),\ lcp(i+1,i+2),\ ...,\ lcp(j-1,j) \bigg\}
\]
至此，我们来考虑 height 的求法
\(height(i) = lcp(i-1,i)\)
设 \(h(i) = height(rk[i])\) ， 第 \(i\) 个后缀与排名在它前一位的后缀的 \(lcp\)
我们考虑第 \(i - 1\) 个后缀，设第 \(k\) 个后缀是排名在它前一位的后缀
则
\[lcp(rk[i-1],rk[k]) = lcp(rk[i],rk[k+1]) + 1
\]
即
\[lcp(rk[i],rk[k]) = h(i-1)- 1
\]
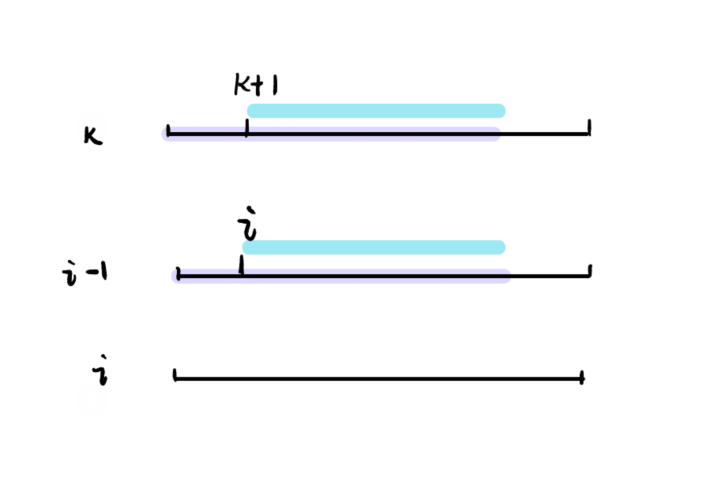
根据之前推的性质，排名在第 \(i\) 个后缀的前一位的后缀不妨在 \(k\) 之前，
有
\[h(i) \ge h(i-1) - 1
\]
有了这一条性质后，我们可以在 \(O(n)\) 时间内求出 height 数组
void get_height()
{
for (int i = 1; i <= n; i++) rk[sa[i]] = i;
for (int i = 1, k = 0; i <= n; i++)
{
if (rk[i] == 1) continue;
if (k) k--; //只需要从 h[i-1] - 1 开始枚举就可以
int j = sa[rk[i] - 1];
while (i + k <= n && j + k <= n && s[i + k] == s[j + k]) k++;
height[rk[i]] = k;
}
}
/*
* @Author: zhl
* @Date: 2020-11-23 15:14:44
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 1000010;
int n, m;
char s[N];
int sa[N], x[N], y[N], c[N], rk[N], height[N];
/*
sa[i] :
x[i] : 第一关键字
y[i] : 第二关键字
c[i] : 桶
rk[i] :
*/
void get_sa(){
/*
根据首字母进行基数排序
*/
for (int i = 1; i <= n; i++) c[x[i] = s[i]] ++;
for (int i = 2; i <= m; i++) c[i] += c[i - 1];
for (int i = n; i; i--) sa[c[x[i]] --] = i; // s[i] = k 表示 rank i 的串从 k 位置开始
/*
开始倍增
*/
for (int k = 1; k <= n; k <<= 1)
{
/*
此时已经根据前k个字母排好序，要根据2*k个字母排好序
先按照后 k 个字母（第二关键字）排序，再根据前 k 个字母排序（稳定排序不会改变相对位置）
*/
int num = 0;
for (int i = n - k + 1; i <= n; i++) y[++num] = i; // 这个区间第二关键字是 空串
for (int i = 1; i <= n; i++) //已经按前 k 个字母排序， 第 i 个后缀的第二关键字是 第 i + k的第一关键字
if (sa[i] > k)
y[++num] = sa[i] - k;
for (int i = 1; i <= m; i++) c[i] = 0;
for (int i = 1; i <= n; i++) c[x[i]] ++;
for (int i = 2; i <= m; i++) c[i] += c[i - 1];
// 按照第二关键字的顺序从后往前枚举
for (int i = n; i; i--) sa[c[x[y[i]]] --] = y[i], y[i] = 0;
swap(x, y); //把 x 暂时存到 y 中
//离散化
x[sa[1]] = 1, num = 1;
for (int i = 2; i <= n; i++)
x[sa[i]] = (y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k]) ? num : ++num;
if (num == n) break;
m = num;
}
}
/*
h[i] = height[rk[i]]
h[i] >= h[i-1] - 1
k 是当前的 h[i]
*/
void get_height()
{
for (int i = 1; i <= n; i++) rk[sa[i]] = i;
for (int i = 1, k = 0; i <= n; i++)
{
if (rk[i] == 1) continue;
if (k) k--; //只需要从 h[i-1] - 1 开始枚举就可以
int j = sa[rk[i] - 1];
while (i + k <= n && j + k <= n && s[i + k] == s[j + k]) k++;
height[rk[i]] = k;
}
}
int main()
{
scanf("%s", s + 1);
n = strlen(s + 1), m = 122;
get_sa();
get_height();
for (int i = 1; i <= n; i++) printf("%d ", sa[i]);
puts("");
for (int i = 1; i <= n; i++) printf("%d ", height[i]);
puts("");
return 0;
}
求所有子串
所有的子串就是所有后缀的所有不同前缀
$ n + 1 -sa[i]$ 是后缀的长度，所有长度在 \(height[i]\) 以内的前缀都被统计过了，所以要减去
int main() {
scanf("%d", &n);
scanf("%s", s + 1);
m = 122;
get_sa();
get_height();
long long ans = 0;
for (int i = 1; i <= n; i++) {
ans += n + 1 - sa[i] - height[i];
}
printf("%lld\n", ans);
}
4.5 后缀自动机
后缀自动机是一个自动机
原串的所有子串和从SAM起点开始的所有路径一一对应，不重不漏。所以终点就是包含所有后缀的点。
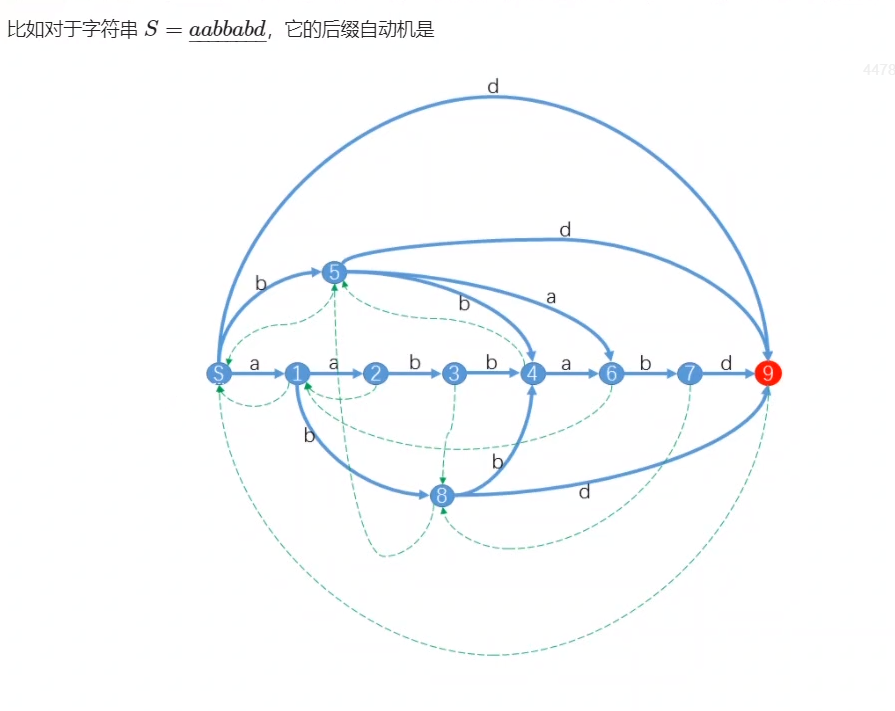
代码中的根节点是 1，上图中是 0，注意区别
一、\(SAM\) 的性质:
\(SAM\) 是个状态机。一个起点，若干终点。原串的所有子串和从 \(SAM\) 起点开始的所有路径一一对应，不重不漏。所以终点就是包含后缀的点。
每个点包含若干子串，每个子串都一一对应一条从起点到该点的路径。且这些子串一定是里面最长子串的连续后缀。
\(SAM\) 问题中经常考虑两种边：
(1) 普通边，类似于 \(Trie\)。表示在某个状态所表示的所有子串的后面添加一个字符。
(2) \(Link、Father\)。表示将某个状态所表示的最短子串的首字母删除。这类边构成一棵树。
二、\(SAM\) 的构造思路
\(endpos(s)\)：子串 \(s\) 所有出现的位置（尾字母下标）集合。\(SAM\) 中的每个状态都一一对应一个 \(endpos\) 的等价类。
\(endpos\) 的性质：
(1) 令 \(s1,s2\) 为 \(S\) 的两个子串 ，不妨设 \(|s1|≤|s2|\) （我们用 \(|s|\) 表示 \(s\) 的长度 ，此处等价于 \(s1\) 不长于 \(s2\) ）。
则 \(s1\) 是 \(s2\) 的后缀当且仅当 \(endpos(s1)⊇endpos(s2)\) ，\(s1\) 不是 \(s2\) 的后缀当且仅当 en\(dpos(s1)∩endpos(s2)=∅\) 。
(2) 两个不同子串的 \(endpos\)，要么有包含关系，要么没有交集。
(3) 两个子串的 \(endpos\) 相同，那么短串为长串的后缀。
(4) 对于一个状态 \(st\) ，以及任意的 \(longest(st)\) 的后缀 s ，如果 \(s\) 的长度满足：\(|shortest(st)|≤|s|≤|longsest(st)| ，\)那么 \(s∈substrings(st)\) 。
算法：
#include<bits/stdc++.h>
using namespace std;
const int N = 2e6 + 10;
struct Edge {
int to, next;
}E[N];
int head[N], cnt;
void addEdge(int from, int to) {
E[cnt] = { to,head[from] };
head[from] = cnt++;
}
int tot = 1, last = 1;
struct Node {
int len, fa;
int ch[26];
}node[N];
typedef long long ll;
char s[N];
ll f[N];
void extend(int c) {
int p = last, np = last = ++tot;
f[tot] = 1;
node[np].len = node[p].len + 1;
for (; p && !node[p].ch[c]; p = node[p].fa) node[p].ch[c] = np;
if (!p)node[np].fa = 1;
else {
int q = node[p].ch[c];
if (node[q].len == node[p].len + 1) node[np].fa = q;
else {
int nq = ++tot;
node[nq] = node[q], node[nq].len = node[p].len + 1;
node[q].fa = node[np].fa = nq;
for (; p and node[p].ch[c] == q; p = node[p].fa) node[p].ch[c] = nq;
}
}
}
ll ans;
void dfs(int u) {
for (int i = head[u]; ~i; i = E[i].next) {
dfs(E[i].to);
f[u] += f[E[i].to];
}
if (f[u] > 1) ans = max(ans, f[u] * node[u].len);
}
int main() {
scanf("%s", s);
for (int i = 0; s[i]; i++)extend(s[i] - 'a');
memset(head, -1, sizeof head);
for (int i = 2; i <= tot; i++) {
addEdge(node[i].fa, i);
}
dfs(1);
printf("%lld\n", ans);
}
询问子串出现次数范围在 \([A,B]\) 内的子串个数
用 \(SAM\) 很简单做，毒瘤题目没有说单组数据多大，就给了个 \(\sum|S| \le 2e6\)
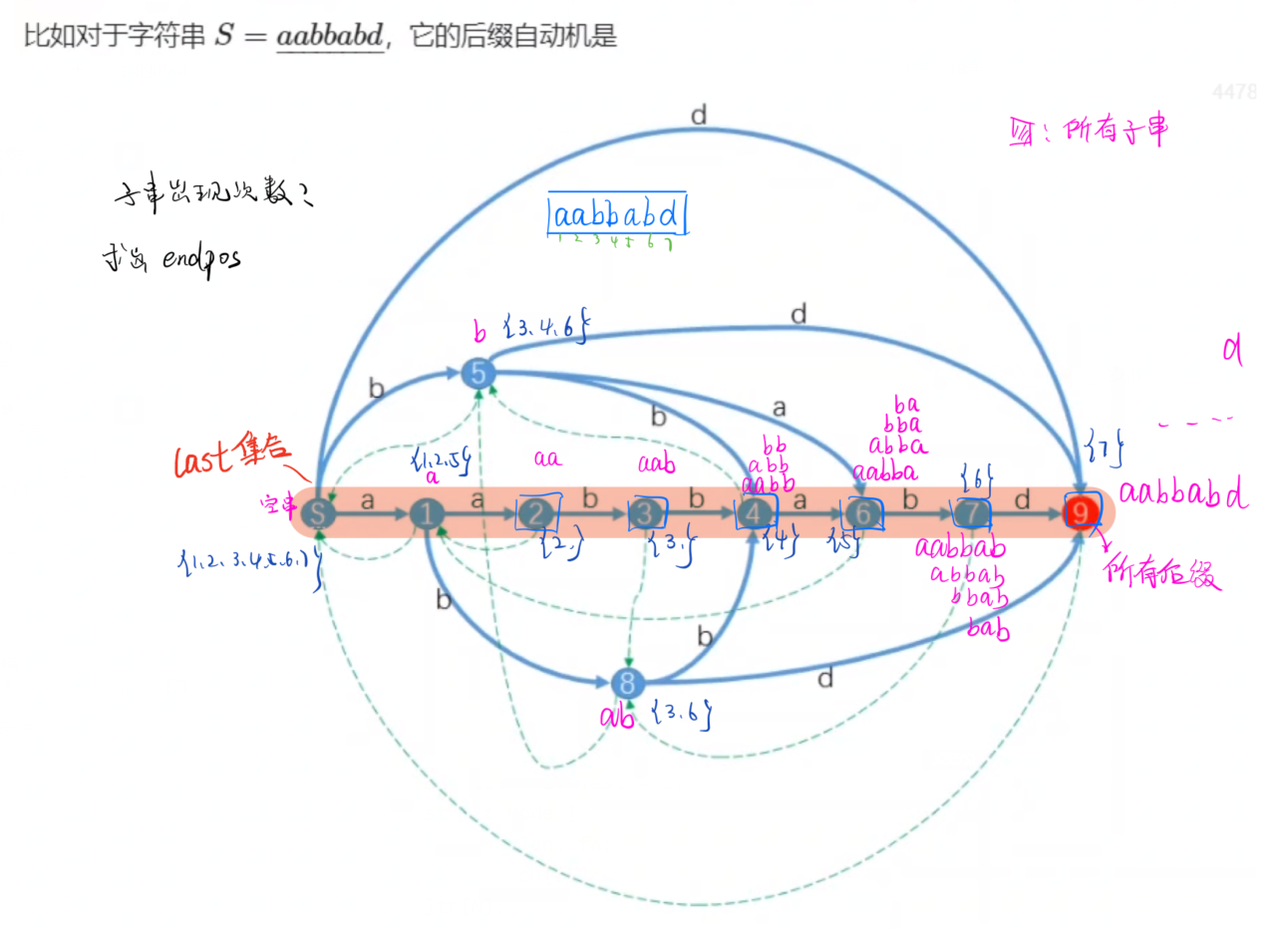
代码中的根节点是 1，上图中是 0，注意区别
图中的 last 集合就是每次的 last
在求 endpos 的时候按照 len 排序就是拓扑序
然后按拓扑序加就可以
/*
* @Author: zhl
* @Date: 2020-11-26 13:30:44
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 4e5 + 10;
int tot = 1, last = 1;
struct Node {
int len, fa;
int ch[26];
}tr[N];
char s[N];
int sum[N], tp[N], cnt[N];
void extend(int c) {
int p = last, np = last = ++tot;
cnt[last] = 1;
tr[np].len = tr[p].len + 1;
for (; p && !tr[p].ch[c]; p = tr[p].fa) tr[p].ch[c] = np;
if (!p)tr[np].fa = 1;
else {
int q = tr[p].ch[c];
if (tr[q].len == tr[p].len + 1) tr[np].fa = q;
else {
int nq = ++tot;
tr[nq] = tr[q]; tr[nq].len = tr[p].len + 1;
tr[q].fa = tr[np].fa = nq;
for (; p and tr[p].ch[c] == q; p = tr[p].fa) tr[p].ch[c] = nq;
}
}
}
void topo() {
for (int i = 1; i <= tr[last].len; i++)sum[i] = 0;
for (int i = 1; i <= tot; i++) sum[tr[i].len]++;
for (int i = 1; i <= tr[last].len; i++)sum[i] += sum[i - 1];
for (int i = 1; i <= tot; i++)tp[sum[tr[i].len]--] = i;
}
void init() {
last = tot = 1;
memset(cnt, 0, sizeof cnt);
memset(tr, 0, sizeof tr);
}
int main() {
while (~scanf("%s", s)) {
init();
int a, b; scanf("%d%d", &a, &b);
for (int i = 0; s[i]; i++) extend(s[i] - 'A');
topo();
long long ans = 0;
for (int i = tot; i >= 1; i--) {
int p = tp[i], fp = tr[p].fa;
cnt[fp] += cnt[p];
if (cnt[p] >= a and cnt[p] <= b) ans += tr[p].len - tr[fp].len;
}
printf("%lld\n", ans);
}
}
求所有子串
每个节点的子串数目是 当前节点的最长长度减去父节点的最长长度。
/*
* @Author: zhl
* @Date: 2020-11-24 10:30:44
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 2e6 + 10;
int tot = 1, last = 1;
struct Node {
int len, fa;
int ch[26];
}tr[N];
typedef long long ll;
char s[N];
ll f[N];
void extend(int c) {
int p = last, np = last = ++tot;
f[tot] = 1;
tr[np].len = tr[p].len + 1;
for (; p && !tr[p].ch[c]; p = tr[p].fa) tr[p].ch[c] = np;
if (!p)tr[np].fa = 1;
else {
int q = tr[p].ch[c];
if (tr[q].len == tr[p].len + 1) tr[np].fa = q;
else {
int nq = ++tot;
tr[nq] = tr[q], tr[nq].len = tr[p].len + 1;
tr[q].fa = tr[np].fa = nq;
for (; p and tr[p].ch[c] == q; p = tr[p].fa) tr[p].ch[c] = nq;
}
}
}
int main() {
int n; scanf("%d", &n);
scanf("%s", s);
for (int i = 0; s[i]; i++)extend(s[i] - 'a');
long long ans = 0;
for (int i = 1; i <= tot; i++) {
ans += tr[i].len - tr[tr[i].fa].len;
}
printf("%lld\n", ans);
}
4.6 回文自动机
回文自动机也叫回文树，可以处理出一个字符串的所有回文子串以及它们的出现次数
/*
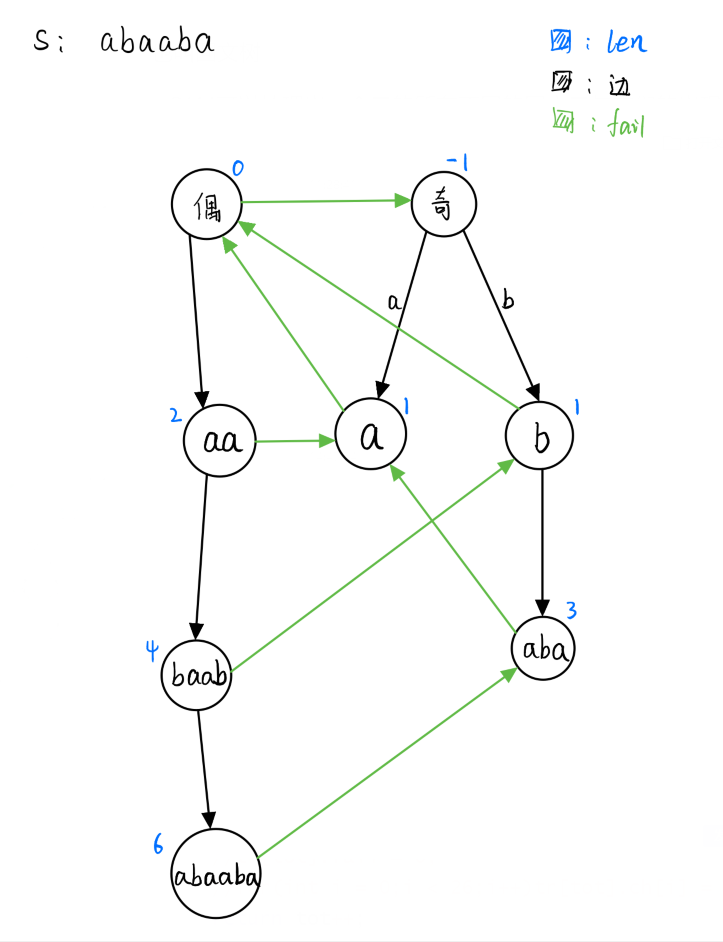
* @Author: zhl
* @Date: 2020-11-24 11:57:26
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 2e6 + 10;
struct Node {
int ch[26], fail;
int len, sum; //这里的sum不是这个串的出现次数，而是回文子串的数目
}tr[N];
char s[N];
int last, tot = 2;
int newnode(int len) {
tr[tot].len = len;
//tr[tot].fail = 0;
//for(int i = 0;i < 26;i++)tr[tot].ch[i] = 0;
return tot++;
}
int getFail(int x, int pos) {
while (s[pos - tr[x].len - 1] != s[pos]) x = tr[x].fail;
return x;
}
void init() {
tr[0].len = 0, tr[1].len = -1;
tr[0].fail = 1; tr[1].fail = 0;
//for(int i = 0;i < 26;i++)tr[0].ch[i] = tr[1].ch[i] = 0;
last = 0;
}
void insert(int pos) {
int cur = getFail(last, pos);
int c = s[pos] - 'a';
if (tr[cur].ch[c] == 0) {
// 出现了新的本质不同的回文串
int now = newnode(tr[cur].len + 2);
tr[now].fail = tr[getFail(tr[cur].fail, pos)].ch[c]; //fail指向后缀中的最长回文串
tr[now].sum = tr[tr[now].fail].sum + 1;
tr[cur].ch[c] = now;
}
last = tr[cur].ch[c];
}
int main() {
scanf("%s", s + 1);
int k = 0; int n = strlen(s + 1);
init();
for (int i = 1; i <= n; i++) {
s[i] = (s[i] - 97 + k) % 26 + 97;
insert(i);
printf("%d ", tr[last].sum);
k = tr[last].sum;
}
}
[P3649 [APIO2014]回文串 - 洛谷 ](https://www.luogu.com.cn/problem/P3649)
求每个回文子串的长度乘出现次数的最大值
/*
* @Author: zhl
* @Date: 2020-11-24 15:09:25
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 2e6 + 10;
struct Node {
int ch[26], fail;
int len, sum;
}tr[N];
char s[N];
int last, tot = 2;
int newnode(int len) {
tr[tot].len = len;
//tr[tot].fail = 0;
//for(int i = 0;i < 26;i++)tr[tot].ch[i] = 0;
return tot++;
}
int getFail(int x, int pos) {
while (s[pos - tr[x].len - 1] != s[pos]) x = tr[x].fail;
return x;
}
void init() {
tr[0].len = 0, tr[1].len = -1;
tr[0].fail = 1; tr[1].fail = 0;
//for(int i = 0;i < 26;i++)tr[0].ch[i] = tr[1].ch[i] = 0;
last = 0;
}
int cnt[N];
void insert(int pos) {
int cur = getFail(last, pos);
int c = s[pos] - 'a';
if (tr[cur].ch[c] == 0) {
int now = newnode(tr[cur].len + 2);
tr[now].fail = tr[getFail(tr[cur].fail, pos)].ch[c]; //fail指向后缀中的最长回文串
tr[now].sum = tr[tr[now].fail].sum + 1;
tr[cur].ch[c] = now;
}
last = tr[cur].ch[c];
cnt[last]++;
}
int main() {
scanf("%s", s + 1);
int n = strlen(s + 1);
init();
for (int i = 1; i <= n; i++) {
insert(i);
}
long long ans = 0;
for (int i = tot; i; i--) { //倒过来其实拓扑序
cnt[tr[i].fail] += cnt[i];
ans = max(ans, 1ll * cnt[i] * tr[i].len);
}
printf("%lld\n", ans);
}
4.7 最小表示法
与字符串 \(S\) 循环同构的字典序最小串
#include<bits/stdc++.h>
using namespace std;
const int N = 3e5 + 10;
int A[N], n;
int mp(int* sec,int n) {
int k = 0, i = 0, j = 1;
while (k < n && i < n && j < n) {
if (sec[(i + k) % n] == sec[(j + k) % n]) {
k++;
}
else {
sec[(i + k) % n] > sec[(j + k) % n] ? i = i + k + 1 : j = j + k + 1;
if (i == j) i++;
k = 0;
}
}
return min(i, j);
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++)scanf("%d", A + i);
int pos = mp(A,n);
for (int i = pos; i < n; i++)printf("%d ", A[i]);
for (int i = 0; i < pos; i++)printf("%d ", A[i]);
}
五、数学
5.0 数论函数
积性函数
如果已知一个函数为数论函数，且\(f(1)=1\)，并且满足以下条件，若对于任意的两个互质的正整数\(p,q\)都满足\(f(p⋅q)=f(p)⋅f(q)\)，那么则称这个函数为积性函数。
常见的积性函数
\(1. \mu(n)\)
莫比乌斯函数
$\mu(1) = 1 $
\(d=\Pi_{i=1}^{k}p_i\)， 且 \(p_i\) 为互异素数时，\(\mu(d) = (-1)^k\)
\(d\) 含有任何质因子的幂次大于等于 \(2\) ,则 \(\mu(d) = 0\)
\(\mu * I = \epsilon\)
$2. \varphi(n) $
欧拉函数
表示 \([1,n)\) 内与 \(n\) 互质的数的个数
\(\varphi * I = id\)
\(\rightarrow \varphi * I * \mu = id * \mu\)
\(\rightarrow \varphi = id * \mu=\sum_{d|n}\mu(d)\cdot \dfrac n d\)
\[\frac{\varphi(n)}{n}=\sum_{d|n}\frac{\mu(d)}{d} \]
\(3. d(n)\)
约数个数
\[d(ij) = \sum_{x|i}\sum_{y|j}[gcd(x,y)=1]
\]
证明：
\[d(n) =\prod_{i=1}^n(1+a_i),\ n = \prod_{i=1}^np_i^{a_i}
\]
\(4. \sigma(n)\)
约数和函数
完全积性函数
\(1. \epsilon(n)\)
元函数, \(\epsilon(n) = [n==1]\)
\(f * \epsilon = f\)
\(2. I(n)\)
恒等函数， \(I(n) = 1\)
\(I * f = \sum_{d|n}f(d)\)
\(3. id(n)\)
单位函数， \(id(n) = n\)
\(lcy\) の \(ppt\)
欧拉函数
\[\varphi(n) = \begin{cases}
1 ,\ \ \ \ \ \ \ \ \ \ \ \ \text{n = 1} \\
numbers(gcd(n,i) == 1 \ for\ i\ \ in\ \ [1,n])
\end{cases}\]
欧拉函数\(\varphi(n)\)等于小于等于n的所有正整数中和n互素的数的个数
一些性质
性质一：
对于素数\(p\)
\[\varphi(p) = p - 1
\]
很显然，除了\(p\) 1到\(p-1\)和都\(p\)互素
性质二：
对于素数\(p\)
\[\varphi(p^k) = p^k - p^{k-1}=p^k(1-\frac1p)
\]
证明:
对于[1,\(p^k\)]中的数n，若与\(p^k\)不互素，则必有
\[n = xp
\]
而\(x\in[1,2,...,p^{k-1}]\)
所以\(\varphi(p^k) = p^k - p^{k-1}\)得证，第一个式子是总数，第二是不互素的数的个数
性质三：（积性）
对于素数\(p\),\(q\)
\[\varphi(p*q) = \varphi(p) \varphi(q)
\]
性质四： (计算公式)
对于任意正整数\(n\) 其中 \(n = \prod_{i=1}^{i = k}p_i^{e_i}\)
\[\varphi(n) = n\prod_{i=1}^{i = k}(1-\frac1{p_i})
\]
计算代码
int euler_phi(int n) {
int m = (int)sqrt(n + 0.5);
int ans = n;
for (int i = 2; i <= m; ++i) {
if (n % i == 0) {
ans = ans / i *(i - 1);
while (n % i == 0) n /= i;
}
}
if (n > 1) ans = ans / n *(n - 1);
return ans;
}
所以在欧拉筛中
if (i % prime[j] == 0) {//因数都一样，多乘了一个p phi[i * prime[j]] = phi[i] * prime[j]; break; } else {//积性 phi[i * phi[j]] = phi[i] * (phi[j] - 1); }
证明:
\[\varphi(n) = \varphi(\prod_{i=1}^{i = k}p_i^{e_i})
\]
\[= \prod_{i=1}^{i = k}\varphi(p_i^{e_i})
\]
\[= \prod_{i=1}^{i = k}(p_i^{e_i}(1-\frac1{p_i}))
\]
\[= n\prod_{i=1}^{i = k}(1-\frac1{p_i})
\]
证毕
性质五:
若 \(i \ mod \ p = 0\)
则
\[\varphi(i*p)=p*\varphi(i)
\]
若 \(i \ mod \ p \neq 0\)
则
\[\varphi(i*p)=(p-1)*\varphi(i)
\]
这条性质显然，由积性直接得出(\(i\),\(p\)互质）
对于第一条性质，首先要知道一个引理：
\[if \ gcd(n,i) = 1 \ then \ gcd(n + i,i) = 1
\]
证明：
若\(n+i\)与\(i\)有公因数\(k\),则\(n\)与\(i\)也有公因数\(k\)，矛盾
由此
若\(gcd(a,b)=1\)，则\(gcd(a,b+ka)=1\)，\(k\in Z\)(\(k\)可以是负数）
因为\(i \ mod \ p = 0\)，所以对于\(k\in[1,i]\)，\(gcd(k,i)=1\)和\(gcd(k,i*p)\)是等价的
又\(gcd(k+xi,i)=1\)，\(x\in[0,1,2,..,p-1]\)
对于\(k>i\)的\(k\)来说，一定是由\(k\in[1,i]\)转移而来
所以 \(\varphi(i*p)=p*\varphi(i)\)
欧拉定理：
若 \(gcd(a,n) == 1\) ，则
\[a^{\varphi(n)} \ mod\ n \ = 1
\]
广义欧拉定理
\[a^b(mod\ n) = \begin{cases}
a^{b\ \% \ \varphi(n)} &(mod\ n),&&a和n互质\\
a^b \ & \ (mod \ n),&&b<\varphi(n)\\
a^{b\ \% \ \varphi(n)+\varphi(n)}&(mod\ n),&&b\ge\varphi(n)
\end{cases}
\]
一般用作降幂，也可以用来求逆元
\(\sum_{d|n} \varphi(d) = n\)
\[\sum_{d|n}\varphi(d) = n
\]
证明：
对于 \(n = 1\) ，不难验证满足题意
对于 \(n = p^a\) ,
\[\sum_{d|n}\varphi(d) = 1 + \sum_{i = 1}^a\varphi(p^i) \\=p^a = n
\]
对于 \(n = p_1^{a_1}...p_k^{a_k}\)
\[\sum_{d|n}\varphi(d) = \sum_{i=0}^{a_1}\varphi(p_1^i)\sum_{i=0}^{a_2}\varphi(p_2^i)...\sum_{i=0}^{a_k}\varphi(p_k^i)\\=p_1^{a_1}...p_k^{a_k} = n
\]
莫比乌斯函数
\[\sum_{d|n}\varphi(d) = \sum_{i=0}^{a_1}\varphi(p_1^i)\sum_{i=0}^{a_2}\varphi(p_2^i)...\sum_{i=0}^{a_k}\varphi(p_k^i)\\=p_1^{a_1}...p_k^{a_k} = n
\]
先介绍莫比乌斯函数 \(\mu\) ，是一个常用的积性函数
\[\mu(x)= \begin{cases}
1,& \text{x = 1}\\
0,& \text{x的任何因子幂次数大于二}\\
(-1)^{k}, & x = \prod_{i=1}^kp_i,p_i为互异的素数
\end{cases}
\]
一、性质
①、常用
\[\sum_{d|n}\mu(d) = [n=1]
\]
其中\([n=1]\)表示n == 1时候成立，为1，否则为0
也就是说任何大于1的整数n，其所有因子的莫比乌斯函数之和为0
②、
对于任意正整数n，
\[\sum_{d|n}\frac{\mu(d)}{d} = \frac{\varphi(n)}{n}
\]
这个性质把莫比乌斯函数和欧拉函数联系在了一起
莫比乌斯反演
定理：
\(F(n)\) 和 \(f(n)\) 是定义在非负整数集合的两个函数，且满足
\[F(n) = \sum_{d|n}f(d)
\]
则有
\[f(n) = \sum_{d|n}\mu(d)F(\frac{n}{d})=\sum_{d|n}\mu(\frac{n}{d})F(d)
\]
利用卷积的性质不难整明
以及
\[\sum_{d|n}\mu(d) = \sum_{i=0}^k(-1)^iC_k^i
\]
\[n = \prod_{i=1}^kp_i^{a_i}
\]
5.1 筛法
线性筛
\(O(n)\) 内筛积性函数与素数
void init() {
mu[1] = phi[1] = 1;
for (int i = 2; i < N; i++) {
if (!vis[i])prime[++cnt] = i, mu[i] = -1, phi[i] = i - 1;
for (int j = 1; j <= cnt and prime[j] * i < N; j++) {
vis[prime[j] * i] = 1;
mu[prime[j] * i] = -mu[i];
phi[prime[j] * i] = (prime[j] - 1) * phi[i];
if (i % prime[j] == 0) {
mu[prime[j] * i] = 0;
phi[prime[j] * i] = phi[i] * prime[j];
break;
}
}
}
for (int i = 1; i < N; i++) sm[i] = sm[i - 1] + mu[i], sp[i] = sp[i - 1] + phi[i];
}
杜教筛
设
\[h = f * g
\]
记 \(S(n) = \sum_{i=1}^{n}f(i)\)
\[\sum_{i=1}^{n}h(i)=\sum_{i=1}^{n}\sum_{d|i}g(d)\cdot f(\frac{i}{d})\\\to =\sum_{d=1}^{n}g(d)\cdot\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}f({i})
\]
\[\to \sum_{i=1}^{n}h(i)=\sum_{d=1}^{n}g(d)\cdot S(\lfloor\frac{n}{d}\rfloor)
\]
\[\sum_{i=1}^{n}h(i)=g(1)\cdot S(n)+\sum_{d=2}^{n}g(d)\cdot S(\lfloor\frac{n}{d}\rfloor)
\]
\[\to g(1)S(n)=\sum_{i=1}^{n}h(i)-\sum_{d=2}^{n}g(d)\cdot S(\lfloor\frac{n}{d}\rfloor)
\]
洛谷模板，筛 \(\mu\) 和 \(\varphi\) 的前缀和
\(\sum_{d|n}\varphi(d) = n\)
\(\sum_{d|n}\mu(d) = [n==1] = \epsilon\)
#include<bits/stdc++.h>
using namespace std;
const int N = 3e6 + 10;
typedef long long ll;
ll prime[N], cnt, mu[N], phi[N], sm[N], sp[N];
bool vis[N];
void init() {
mu[1] = phi[1] = 1;
for (int i = 2; i < N; i++) {
if (!vis[i])prime[++cnt] = i, mu[i] = -1, phi[i] = i - 1;
for (int j = 1; j <= cnt and prime[j] * i < N; j++) {
vis[prime[j] * i] = 1;
mu[prime[j] * i] = -mu[i];
phi[prime[j] * i] = (prime[j] - 1) * phi[i];
if (i % prime[j] == 0) {
mu[prime[j] * i] = 0;
phi[prime[j] * i] = phi[i] * prime[j];
break;
}
}
}
for (int i = 1; i < N; i++) sm[i] = sm[i - 1] + mu[i], sp[i] = sp[i - 1] + phi[i];
}
unordered_map<ll, ll>M, P;
ll m(ll n) {
if (n < N)return sm[n];
if (M.count(n)) return M[n];
ll ans = 1;
for (ll l = 2, r; l <= n; l = r + 1) {
r = n / (n / l);
ans -= (r - l + 1) * m(n / l);
}
return M[n] = ans;
}
ll p(ll n) {
if (n < N)return sp[n];
if (P.count(n)) return P[n];
ll ans = n * (n + 1) / 2;
for (ll l = 2, r; l <= n; l = r + 1) {
r = n / (n / l);
ans -= (r - l + 1) * p(n / l);
}
return P[n] = ans;
}
ll T, n;
int main() {
init();
scanf("%lld", &T);
while (T--) {
scanf("%lld", &n);
printf("%lld %lld\n", p(n), m(n));
}
}
Min_25
思想：
\[\sum_{i=1}^nf(i) = \sum_{i \in Prime}f(i) + \sum_{i \notin Prime}f(i)
\]
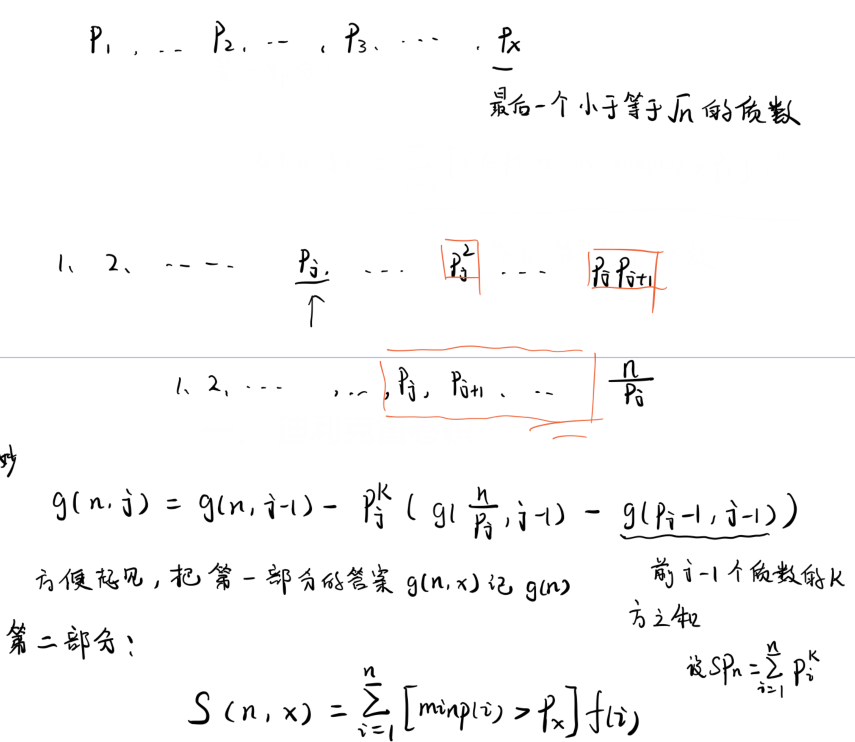
分为两个部分，第一部分是所有素数，第二部分是所有的合数
第一部分
搞来一个这样的函数 \(g(n,j)\)
\[g(n,j) = \sum_{i=1}^n[i \in Prime\ or\ minp(i) > P_j] i^k
\]
所有的素数加上满足\(minp(i) > P_j\) 的所有 \(i\)
\([1-n]\) 中所有质数的 \(k\) 次方之和就是 \(g(n,x)\) ，\(P_x\) 是最后一个小于等于
\(\sqrt n\) 的质数
考虑 \(g(n,j)\) 的转移
\[g(n,j) = g(n,j-1) - P_j^k\bigg(g(\dfrac n {P_j},j-1)\ -g(P_j-1,j-1)\bigg)
\]
这个东西自己在纸上写一些体会一下，注意 \(P_j\) 筛去的第一个数是 \(P_j^2\) , 第二个数不是 \(P_j^2+ P_j\)
第二部分
设
\[S(n,x) = \sum_{i=1}^n[minp(i) > P_x]f(i)
\]
可以把 \(S(n,x)\) 也分成两部分，一部分是所有大于 \(P_x\) 的质数，另一部分是最小质因数大于 \(P_x\) 的合数，枚举最小质因子
\[S(n,x) = g(n) - sp_x + \sum_{p_k^e \le n \&k>n}f(p_k^e)\bigg(S \bigg(\dfrac n {p_k^e}\bigg) + [e \ne 1]\bigg)
\]
当 \(e = 1\) 的时候， \(P_k\) 在前面枚举过了，不等于 \(1\) 时，需要加上 \(P_k^e\)
存下所有可能的 \(\lfloor\dfrac n x \rfloor\) , 做一个映射
\[idx(x)= \begin{cases}ind1[x] , \ \ x\le \sqrt n \\ind2[n/x],\ \ x>\sqrt n\end{cases}
\]
min25模板
积性函数 \(f\) ， \(f(p^k) = p^k(p^k-1)\)
求 \(\sum_{i=1}^nf(i)\)
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll mod = 1e9 + 7, inv6 = 166666668, inv2 = 500000004;
const int maxn = 1e6 + 10;
ll n, sqr;
ll prime[maxn], cnt, vis[maxn];
ll sp1[maxn], sp2[maxn];//sp1 p的前缀和，sp2 p^2的前缀和
ll w[maxn], tot;
ll g1[maxn], g2[maxn], ind1[maxn], ind2[maxn];
void get(int maxn) {
for (int i = 2; i <= maxn; i++) {
if (!vis[i]) {
prime[++cnt] = i;
sp1[cnt] = (sp1[cnt - 1] + i) % mod;
sp2[cnt] = (sp2[cnt - 1] + 1ll * i * i) % mod;
}
for (int j = 1; j <= cnt && prime[j] * i <= maxn; j++) {
vis[prime[j] * i] = 1;
if (i % prime[j] == 0)break;
}
}
}
ll S(ll x, int y){
if (prime[y] >= x)return 0;
ll k = x <= sqr ? ind1[x] : ind2[n / x];
ll ans = (g2[k] - g1[k] + mod - (sp2[y] - sp1[y]) + mod) % mod;
for (int i = y + 1; i <= cnt && prime[i] * prime[i] <= x; i++)
{
ll pe = prime[i];
for (int e = 1; pe <= x; e++, pe = pe * prime[i])
{
ll xx = pe % mod;
ans = (ans + xx * (xx - 1) % mod * (S(x / pe, i) + (e != 1))) % mod;
}
}
return ans % mod;
}
int main() {
scanf("%lld", &n);
sqr = sqrt(n);
get(sqr);
for (ll l = 1, r; l <= n; l = r + 1) {
r = n / (n / l);
w[++tot] = n / l;
ll k = w[tot] % mod;
g1[tot] = (k * (k + 1) % mod * inv2 - 1 + mod) % mod;
g2[tot] = (k * (k + 1) % mod * (2 * k + 1) %mod * inv6 % mod + mod - 1) % mod;
if (w[tot] <= sqr)ind1[n / l] = tot;
else ind2[n / (n / l)] = tot;
}
for (int i = 1; i <= cnt; i++) {
//g(n,j) 滚第一维
for (int j = 1; j <= tot && prime[i] * prime[i] <= w[j]; j++) {
ll k = w[j] / prime[i] <= sqr ? ind1[w[j] / prime[i]] : ind2[n / (w[j] / prime[i])];
g1[j] -= prime[i] * (g1[k] - sp1[i - 1] + mod) % mod;
g2[j] -= prime[i] * prime[i] % mod * (g2[k] - sp2[i - 1] + mod) % mod;
g1[j] %= mod; g2[j] %= mod;
if (g1[j] < 0)g1[j] += mod;
if (g2[j] < 0)g2[j] += mod;
}
}
printf("%lld\n", (S(n, 0) + 1) % mod);
}
5.2 扩展欧几里得
欧几里得算法
int gcd(int a,int b){
return b == 0 ? a : gcd(b, a % b);
}
时间复杂度是 \(O(logn)\) 的
扩展欧几里得
\[ax + by = c
\]
设 \(g = gcd(a,b)\) , 有 \(g\ \ | \ \ (ax + by)\) , 若 \(g\) 不整除 \(c\) ,则方程没有整数解
否则，可以用 Exgcd 求解出
\[ax + by = g
\]
的一组特解 \((x_0,y_0)\)
而原方程对应的一组特解
\[\begin{cases}x_1 = \dfrac {x_0c} g \\ \\ y_1 = \dfrac {y_0c}g \end{cases}
\]
原方程的通解为
\[\begin{cases}x = x_1 + \dfrac {sb} g \\ \\ y = y_1 - \dfrac {sa}g \end{cases}
\]
int exgcd(int a, int b, int& x, int& y) {
//ax + by = gcd(a,b) 求解一组特解 x , y
if (!b) {
x = 1;
y = 0;
return a;
}
int d = exgcd(b, a % b, x, y);
int t = x;
x = y;
y = t - (a / b) * y;
return d;
}
5.3 扩展中国剩余定理
中国剩余定理
问题
$x\equiv a_1 ( mod\ m_1) $
\(x \equiv a_2(mod\ m_2)\)
\(......\)
\(x \equiv a_k(mod\ m_k)\)
其中 \(m\) 两两互素
int CRT(){
int res = 0,M = 1;
int x,y,gcd;
for(int i = 1;i <= k;i++){
M *= m[i];
}
for(int i = 1;i <= k;i++){
int tmp = M / m[i];
ex_gcd(tp,m[i],gcd,x,y);
x = (x % m[i] + m[i]) % m[i];
res = (res + tmp * a[i] * x) % M;
}
return (res + M) % M;
}
扩展中国剩余定理
取消了两两互素的限制
/*
* @Author: zhl
* @LastEditTime: 2020-11-30 18:32:04
*/
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5 + 10;
typedef long long ll;
ll A[N], m[N];
/*
x = A1 % m1
x = A2 % m2
......
x = An % mn
求解 x
*/
void ex_gcd(int a, int b, int& gcd, int& x, int& y) {
if (b == 0) {
x = 1;
y = 0;
gcd = a;
}
else {
ex_gcd(b, a % b, gcd, y, x); //a,b交换，x,y跟着交换，大概应该是这个意思
y -= x * (a / b);
}
}
ll mul(ll a, ll b, ll p) {
ll ans = 0;
while (b) {
if (b & 1)ans = (ans + a) % p;
a = (a + a) % p;
b >>= 1;
}
if (ans < 0)ans += p;
return ans;
}
int n;
ll EX_CRT() {
int x, y, gcd;
int M = m[1]; int res = A[1];
for (int i = 2; i <= n; i++) {
int a = M, b = m[i], c = ((A[i] - res) % b + b) % b;
ex_gcd(a, b, gcd, x, y);
int tmp = b / gcd;
if (c % gcd != 0) return -1; //方程无解
x = mul(x, c / gcd, tmp); //因为系数不为1
res += x * M;
M *= tmp;
res = (res % M + M) % M;
}
return (res % M + M) % M;
}
signed main() {
scanf("%lld", &n);
for (int i = 1; i <= n; i++) {
scanf("%lld%lld", m + i, A + i);
}
printf("%lld\n", EX_CRT());
}
5.4 莫比乌斯反演
两种形式
Ⅰ
\[F(n) = \sum_{d|n}f(d) \to f(n)=\sum_{d|n}\mu(d)F(\dfrac nd)
\]
Ⅱ
\[F(n)=\sum_{n|d}f(d) \to f(n) = \sum_{n|d}\mu(\dfrac dn)F(d)
\]
基本上就是围绕
\[\sum_{d|n}\mu(d) = [n==1]
\]
和
\[\sum_{d|n}\varphi(d) = n
\]
进行展开
例1
求
\[\sum_{i=1}^n\sum_{j=1}^m[gcd(i,j) == 1] \ \ \ \ \ \ \ (n < m)
\]
直接替换
\[\sum_{i=1}^n\sum_{j=1}^m\sum_{d|gcd(i,j)}\mu(d)
\]
枚举 \(d\) ，这里比较套路
\[\sum_{d=1}^n\mu(d)*\lfloor \dfrac n d \rfloor * \lfloor \dfrac m d \rfloor
\]
可以 \(O(\sqrt n)\) 处理了
例2
\[\sum_{i=1}^n\sum_{j=1}^m[gcd(i,j) == k]
\]
与上面那个一样
\[\sum_{i=1}^{\lfloor\dfrac n k \rfloor}\sum_{j=1}^{\lfloor \dfrac m k \rfloor}[gcd(i,j) == 1]
\]
例3
\[\sum_{i=1}^n\sum_{j=1}^mgcd(i,j)
\]
\[\sum_{i=1}^n\sum_{j=1}^m\sum_{d|gcd(i,j)}\varphi(d)
\]
\[= \sum_{d = 1}^n\varphi(d)*\lfloor \dfrac n d \rfloor * \lfloor \dfrac m d \rfloor
\]
5.5 生成函数
生成函数
在数学中，某个序列\((a_n)_{n∈N}\) 的母函数（又称生成函数，英语：\(Generating\ function\)）是一种形式幂级数，其每一项的系数可以提供关于这个序列的信息。
普通生成函数
有三种物品，分别有 3 ，2， 3个，问拿四个的方案数
f[i][j] 表示当前第 i 个位置，已经选了 j 个物品的方案数
f[0][0] = 1;
for(int i = 1;i <= 3;i++){
for(int j = 0;j <= 8;j++){//总共要选j个
for(int k = 0;k <= j;k++){//已经选了k个
if(j - k <= v[i])//此时要选j-k个
f[i][j] += f[i-1][k];
}
}
}
第一种物品的生成函数 \(G_1(x) = 1 + x + x^2 + x ^ 3\)
\(G_2(x) = 1 + x + x^2\) , $G_3 = 1 + x + x^2 + x^3 $
\(G_1(x)*G_2(x)*G_3(x)\) ,中 \(x^4\) 的系数就是答案
上述代码其实就是在求多项式乘法的系数
指数生成函数
将上述问题改成排列方案hdu1521
构造出
\(G_1(x) = 1+\frac{x^1}{1} + \frac{x^2}{2!} + \frac{x^3}{3!}\)
\(G_2(x) = 1 + \frac{x^1}{1} + \frac{x^2}{2}\)
\(G_3(x) = 1 + \frac{x^1}{1} + \frac{x^2}{2!} + \frac{x^3}{3!}\)
\[\begin{aligned}G_e(x) &= (1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!})(1+\frac{x}{1!} + \frac{x^2}{2!}) (1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!})\\ &= (1+2x+2x^2+\frac{7}{6}x^3 + \frac{5}{12}x^4 + \frac{1}{12}x^5) (1+x+\frac{1}{2}x^2 + \frac{1}{6}x^3)\\ &=(1+3x + \frac{9}{2}x^2 + \frac{14}{3}x^3 + \frac{35}{12}x^4 + \frac{17}{12}x^5 + \frac{35}{72} x^6 + \frac{8}{72}x^7 + \frac{1}{71}x^8)\end{aligned}
\]
答案就是 \(x^4\) 的系数乘上 \(4!\) ， \(\frac{35}{12} * 4! = 70\)
(1-x)^-1 型
\[\dfrac 1 {1-x} = \sum_{i=0}^\infty x^i
\]
广义二项式定理
\[\dfrac 1 {(1-x)^n} = \sum_{i=0}^{\infty} C_{n+i-1}^i x^i
\]
至多为 \(k\) 就是 \(\dfrac {1-x^{k+1}} {1-x}\) ， 就是 \(1 + x + x^2 + x^3 + ... + x^k\)
\(k\) 的倍数就是 \(\dfrac 1 {1-x^k}\) , 就是
\(1 + x^k + x^{2k} + ...\)
最后的结果是 \(\dfrac 1 {(1-x)^5}\) ， 带入广义二项式定理， 答案是 \(C_n^4\)
\(py\) 草不过去， \(OI\) 爷直呼 人生苦短， \(ruby\) 用我
e^x 型
\[e^x = \sum_{i=0}^\infty \dfrac {x^i} {i!}
\]
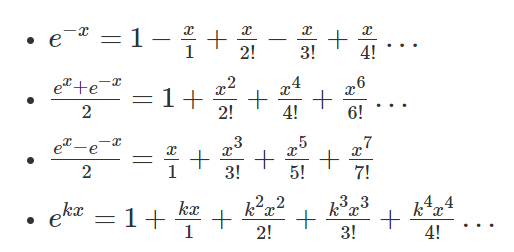
5.6 矩阵
主要是一些矩阵模拟题目，还有矩阵快速幂加速数列计算。
struct mat {
static const int _N = 100;
int n;
int m[_N][_N];
// ll m[_N][_N];
mat() {}
mat(int _n, int _v = 1) {
n = _n;
memset(m, 0, sizeof m);
if (_v == 1)for (int i = 0; i < _n; i++)m[i][i] = 1;
}
mat(vector<vector<int>>A, int _n) {
n = _n;
for (int i = 0; i < n; i++)for (int j = 0; j < n; j++)m[i][j] = A[i][j];
}
void input() {
for (int i = 0; i < n; i++)for (int j = 0; j < n; j++)scanf("%d", &m[i][j]);
}
void print() {
for (int i = 0; i < n; i++)for (int j = 0; j < n; j++)printf("%d%c", m[i][j], " \n"[j == n - 1]);
}
mat operator *(const mat& b)const {
mat res(n, 0);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) {
//这里会爆 int
res.m[i][j] = (res.m[i][j] + 1ll * m[i][k] * b.m[k][j] % mod) % mod;
}
}
}
return res;
}
mat pow(ll p) {
mat a = *this, res = mat(n);
while (p) {
if (p & 1)res = res * a;
a = a * a;
p >>= 1;
}
return res;
}
};
5.7 快速傅里叶变换
FFT 可以用来加速多项式乘法， 时间复杂度 \(O(nlogn)\)
FFT 快速傅里叶变换
\(O(nlogn)\) 计算多项式乘法
由 系数表示法 转换为 点值表示法
记
\[\omega_n^k = cos(\dfrac {2\pi\cdot k} n) + i \cdot sin(\dfrac {2\pi \cdot k} n)
\]
\[A(x)=a_0+a_1*x+a_2*{x^2}+a_3*{x^3}+a_4*{x^4}+a_5*{x^5}+\\ \dots+a_{n-2}*x^{n-2}+a_{n-1}*x^{n-1}
\]
\[A(x)=(a_0+a_2*{x^2}+a_4*{x^4}+\dots+a_{n-2}*x^{n-2})+\\(a_1*x+a_3*{x^3}+a_5*{x^5}+ \dots+a_{n-1}*x^{n-1})
\]
设
\[A_1(x)=a_0+a_2*{x}+a_4*{x^2}+\dots+a_{n-2}*x^{\frac{n}{2}-1}
\]
\[A_2(x)=a_1+a_3*{x}+a_5*{x^2}+ \dots+a_{n-1}*x^{\frac{n}{2}-1}
\]
则
\[A(x)=A_1(x^2)+xA_2(x^2)
\]
带入 \(x = \omega_n^k\)
\[A(\omega_n^k) = A_1(\omega_{\frac n2}^k) + \omega_n^kA_2(\omega_{\frac n2}^k)
\]
带入 $x = \omega_n^{k+\frac n2} $
\[A(\omega_n^{k+\frac n2}) = A_1(\omega_{\frac n2}^k) -\omega_n^kA_2(\omega_{\frac n2}^k)
\]
也就是说如果知道了 $A_1(x),A_2(x) $ 分别在 \(\omega_{\frac n2}^0\) , \(\omega_{\frac n2}^1\) , \(\omega_{\frac n2}^2\) ,...,\(\omega_{\frac n2}^{\frac n2 -1}\) 的取值，
就可以 \(O(n)\) 的求出 \(A(x)\)
void fft(cp *a,int n,int inv)//inv是取共轭复数的符号
{
if (n==1)return;
int mid=n/2;
static cp b[MAXN];
for(int i = 0;i < mid;i++)b[i]=a[i*2],b[i+mid]=a[i*2+1];
for(int i = 0;i < n;i++)a[i]=b[i];
fft(a,mid,inv),fft(a+mid,mid,inv);//分治
for(int i = 0;i < mid;i++)
{
cp x(cos(2*pi*i/n),inv*sin(2*pi*i/n));//inv取决是否取共轭复数
b[i]=a[i]+x*a[i+mid],b[i+mid]=a[i]-x*a[i+mid];
}
for(int i = 0;i < a;i++)a[i]=b[i];
}
每个位置分治后最终的位置是二进制翻转后的位置
void fft(cp *a,int n,int inv)
{
int bit=0;
while ((1<<bit)<n)bit++;
fo(i,0,n-1)
{
rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));
if (i<rev[i])swap(a[i],a[rev[i]]);//不加这条if会交换两次（就是没交换）
}
for (int mid=1;mid<n;mid*=2)//mid是准备合并序列的长度的二分之一
{
cp temp(cos(pi/mid),inv*sin(pi/mid));//单位根，pi的系数2已经约掉了
for (int i=0;i<n;i+=mid*2)//mid*2是准备合并序列的长度，i是合并到了哪一位
{
cp omega(1,0);
for (int j=0;j<mid;j++,omega*=temp)//只扫左半部分，得到右半部分的答案
{
cp x=a[i+j],y=omega*a[i+j+mid];
a[i+j]=x+y,a[i+j+mid]=x-y;//这个就是蝴蝶变换什么的
}
}
}
}
注意 lim
#include<bits/stdc++.h>
using namespace std;
const double pi = acos(-1.0);
const int N = 3e6 + 10;
struct cp {
double x, y;
cp() {}
cp(double _x, double _y) {
x = _x; y = _y;
}
cp operator + (cp b) {
return cp(x + b.x, y + b.y);
}
cp operator -(cp b) {
return cp(x - b.x, y - b.y);
}
cp operator *(cp b) {
return cp(x * b.x - y * b.y, x * b.y + y * b.x);
}
};
int rev[N];
int bit = 0;
int lim;
void FFT(cp* a, int inv) {
for (int i = 0; i < lim; i++) {
if (i < rev[i]) {
swap(a[i], a[rev[i]]);
}
}
for (int mid = 1; mid < lim; mid <<= 1) {
cp temp(cos(pi / mid), inv * sin(pi / mid));
for (int i = 0; i < lim; i += mid * 2) {
cp omega(1, 0);
for (int j = 0; j < mid; j++, omega = omega * temp) {
cp x = a[i + j], y = omega * a[i + j + mid];
a[i + j] = x + y, a[i + j + mid] = x - y;
}
}
}
}
int n, m;
cp A[N], B[N];
int main() {
scanf("%d%d", &n, &m);
lim = 1;
while (lim <= n + m)lim<<=1,bit++;//调整至 2^k
for (int i = 0; i < lim; i++) {
rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
}
for (int i = 0; i <= n; i++)scanf("%lf", &A[i].x), A[i].y = 0;
for (int i = 0; i <= m; i++)scanf("%lf", &B[i].x), B[i].y = 0;
FFT(A, 1);
FFT(B, 1);
for (int i = 0; i <= lim; i++) {
A[i] = A[i] * B[i];
}
FFT(A, -1);
for (int i = 0; i <= n + m; i++) {
printf("%d ", int(A[i].x /lim+0.5));
}
}
NTT
原根
还没有整太明白
待补，丢一个板子
#include<bits/stdc++.h>
#define swap(a,b) (a^=b,b^=a,a^=b)
using namespace std;
#define LL long long
const int MAXN = 3 * 1e6 + 10, P = 998244353, G = 3, Gi = 332748118;
char buf[1 << 21], * p1 = buf, * p2 = buf;
int N, M, limit = 1, L, r[MAXN];
LL a[MAXN], b[MAXN];
inline LL fastpow(LL a, LL k) {
LL base = 1;
while (k) {
if (k & 1) base = (base * a) % P;
a = (a * a) % P;
k >>= 1;
}
return base % P;
}
inline void NTT(LL* A, int type) {
for (int i = 0; i < limit; i++)
if (i < r[i]) swap(A[i], A[r[i]]);
for (int mid = 1; mid < limit; mid <<= 1) {
LL Wn = fastpow(type == 1 ? G : Gi, (P - 1) / (mid << 1));
for (int j = 0; j < limit; j += (mid << 1)) {
LL w = 1;
for (int k = 0; k < mid; k++, w = (w * Wn) % P) {
int x = A[j + k], y = w * A[j + k + mid] % P;
A[j + k] = (x + y) % P,
A[j + k + mid] = (x - y + P) % P;
}
}
}
}
int main() {
scanf("%d%d", &N, &M);
for (int i = 0; i <= N; i++) scanf("%d", a + i);
for (int i = 0; i <= M; i++) scanf("%d", b + i);
while (limit <= N + M) limit <<= 1, L++;
for (int i = 0; i < limit; i++) r[i] = (r[i >> 1] >> 1) | ((i & 1) << (L - 1));
NTT(a, 1); NTT(b, 1);
for (int i = 0; i < limit; i++) a[i] = (a[i] * b[i]) % P;
NTT(a, -1);
LL inv = fastpow(limit, P - 2);
for (int i = 0; i <= N + M; i++)
printf("%d ", (a[i] * inv) % P);
return 0;
}
C - Triple
题意
给三个数组 \(A,B,C\) 问有多少个 \((i,j,k)\) 使得
\(A_i,B_j,C_k\) 中较小的两个数的和大于等于最大的数
\(1 \le T \le 100\)
\(1 \le A_i,B_i,C_i,n \le 100,000\)
There are at most \(20\) test cases with \(N>1000\)
思路
用容斥思想，所有不和法的方案就是 较小的两数相加小于第三个数的方案。
处理出 所有的 \(A_i + B_j\) ，然后对于每一个 \(C_k\) ,只要加上所有小于 \(C_k\) 的方案数就可以
这里小数据用暴力，大数据用 多项式乘法
/*
* @Author: zhl
* @Date: 2020-11-09 15:23:52
*/
#include<bits/stdc++.h>
#define rep(i,a,b) for(int i = a;i <= b;i++)
#define mem(a,b) memset((a),(b),sizeof(a))
using namespace std;
typedef long long ll;
const double pi = acos(-1.0);
const int N = 6e5 + 10;
struct cp {
double x, y;
cp() {}
cp(double _x, double _y) {
x = _x; y = _y;
}
cp operator + (cp b) {
return cp(x + b.x, y + b.y);
}
cp operator -(cp b) {
return cp(x - b.x, y - b.y);
}
cp operator *(cp b) {
return cp(x * b.x - y * b.y, x * b.y + y * b.x);
}
};
int rev[N];
int bit = 0;
int lim;
void FFT(cp* a, int inv) {
for (int i = 0; i < lim; i++) {
if (i < rev[i]) {
swap(a[i], a[rev[i]]);
}
}
for (int mid = 1; mid < lim; mid <<= 1) {
cp temp(cos(pi / mid), inv * sin(pi / mid));
for (int i = 0; i < lim; i += mid * 2) {
cp omega(1, 0);
for (int j = 0; j < mid; j++, omega = omega * temp) {
cp x = a[i + j], y = omega * a[i + j + mid];
a[i + j] = x + y, a[i + j + mid] = x - y;
}
}
}
}
int T, n, A[N], B[N], C[N], tA[N], tB[N], tC[N];
cp x[N], y[N];
ll sum[N];
ll solve_small(int* a, int* b, int* c) {
for (int i = 0; i <= c[n - 1]; i++)sum[i] = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
sum[a[i] + b[j]]++;
}
}
ll ans = 0;
for (int i = 1; i <= c[n - 1]; i++)sum[i] += sum[i - 1];
for (int i = 0; i < n; i++) ans += sum[c[i] - 1];
return ans;
}
ll solve_big(int* a, int* b, int* c) {
for (int i = 0; i <= lim; i++)x[i] = cp(a[i], 0), y[i] = cp(b[i], 0);
FFT(x, 1); FFT(y, 1);
for (int i = 0; i <= lim; i++)x[i] = x[i] * y[i];
FFT(x, -1);
mem(sum, 0);
ll ans = 0;
for (int i = 0; i <= c[n - 1]; i++)sum[i] = signed(x[i].x / lim + 0.5);
for (int i = 1; i <= c[n - 1]; i++)sum[i] += sum[i - 1];
for (int i = 0; i < n; i++) ans += sum[c[i] - 1];
return ans;
}
int main() {
scanf("%d", &T); int c = 0;
while (T--) {
scanf("%d", &n);
mem(tA, 0); mem(tB, 0); mem(tC, 0);
lim = 1; bit = 0;
while (lim <= (2 * n))lim <<= 1, bit++;
mem(rev, 0);
for (int i = 0; i < lim; i++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
for (int i = 0; i < n; i++)scanf("%d", A + i), tA[A[i]]++; sort(A, A + n);
for (int i = 0; i < n; i++)scanf("%d", B + i), tB[B[i]]++; sort(B, B + n);
for (int i = 0; i < n; i++)scanf("%d", C + i), tC[C[i]]++; sort(C, C + n);
printf("Case #%d: ", ++c);
if (n <= 1000) {
printf("%lld\n", 1ll * n * n * n - solve_small(A, B, C) - solve_small(A, C, B) - solve_small(B, C, A));
}
else {
printf("%lld\n", 1ll * n * n * n - solve_big(tA, tB, C) - solve_big(tA, tC, B) - solve_big(tB, tC, A));;
}
}
}
5.8 素数测试
复杂度...非常低
Miller_Rabin 判断素数
Pollard_Rho 分解质因数
/*
* @Author: zhl
* @Date: 2020-11-03 11:43:54
*/
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5 + 5;
int x[105];
int mul(int a, int b, int p){
int ans = 0;
while (b){
if (b & 1LL) ans = (ans + a) % p;
a = (a + a) % p;
b >>= 1;
}
return ans;
}
int qpow(int a, int b, int p){
int ans = 1;
while (b){
if (b & 1LL) ans = mul(ans, a, p);
a = mul(a, a, p);
b >>= 1;
}
return ans;
}
bool Miller_Rabin(int n){
if (n == 2) return true;
int s = 20, i, t = 0;
int u = n - 1;
while (!(u & 1))
{
t++;
u >>= 1;
}
while (s--)
{
int a = rand() % (n - 2) + 2;
x[0] = qpow(a, u, n);
for (i = 1; i <= t; i++)
{
x[i] = mul(x[i - 1], x[i - 1], n);
if (x[i] == 1 && x[i - 1] != 1 && x[i - 1] != n - 1)
return false;
}
if (x[t] != 1) return false;
}
return true;
}
int gcd(int a, int b){
return b ? gcd(b, a % b) : a;
}
int Pollard_Rho(int n, int c){
int i = 1, k = 2, x = rand() % (n - 1) + 1, y = x;
while (1){
i++;
x = (mul(x, x, n) + c) % n;
int p = gcd((y - x + n) % n, n);
if (p != 1 && p != n) return p;
if (y == x) return n;
if (i == k){
y = x;
k <<= 1;
}
}
}
map<int, int> m;
void find(int n, int c = 12345)
{
if (n == 1) return;
if (Miller_Rabin(n)){
m[n]++;
return;
}
int p = n, k = c;
while (p >= n) p = Pollard_Rho(p, c--);
find(p, k);
find(n / p, k);
}
int T,n;
int main(){
cin >> T;
while(T--){
cin >> n;
if(Miller_Rabin(n)){
cout << "Prime" << endl;
}else{
m.clear();
find(n);
cout << (*m.rbegin()).first << endl;
}
}
}
5.9 拉格朗日插值
\(n\) 阶的多项式 \(f(x)\) 可以由 \(n+1\) 个点确认。
若现有 \(n+1\) 个点 \((x_i,y_i) \ \ , \ i \in [0,n]\) 在 \(f(x)\) 上
则可以计算任意值 \(k\) 的函数值 \(f(k)\)
\[f(k) = \sum_{i=0}^ny_i\prod_{j\ne i}\dfrac {k-x_j} {x_i - x_j}
\]
例如二次函数 \(f(x)\) 经过了 \((1,4) , (2,9) , (3,16)\) 三个点，则带入公式中
\[f(k) = 4\dfrac {(k-2)(k-3)}{(1-2)(1-3)} + 9\dfrac{(k-1)(k-3)}{(2-1)(2-3)} + 16 \dfrac {(k-1)(k-2)}{(3-1)(3-2)}
\]
不难看出，当 \(k = x_i\) 的时候， \(f(k) = y_i\) ,且\(f(k)\) 是二次函数。
所以正确性可以保证
这样计算的时间复杂度是 \(O(n^2)\)
特殊情况
若 \(x_i = i\) ， 即 \(n\) 阶多项式 \(f(x)\) 在 \(0,1,2,...,n - 1\) 处的函数值
则
\[f(k) = \sum_{i=0}^ny_i\prod_{j\ne i}\dfrac {k-j} {i - j}
\]
我们考虑 \(\prod_{j\ne i}\dfrac {k-j} {i - j}\) 的计算
对于某个 \(k\) ,我们可以预处理出 \(k - j\) 的前缀积和后缀积。分母是 \(i!(n-i)!(-1)^{n-i}\)
时间复杂度 \(O(n)\)
先算出 \(f(n+1)\) ,然后就有了 \(S(1),...,S(n+1)\) 就可以用 \(S\) 插值计算 \(S(R) - S(L-1)\)
/*
* @Author: zhl
* @Date: 2020-11-12 14:50:58
*/
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod = 9999991, N = 1e3 + 10;
int y[N], S[N];
int qpow(int a, int p) {
int ans = 1;
while (p) {
if (p & 1)ans = (ans * a) % mod;
a = (a * a) % mod;
p >>= 1;
}
return ans;
}
int fac[N], invf[N];
void init() {
fac[0] = invf[0] = 1;
for (int i = 1; i < N; i++) {
fac[i] = i * fac[i - 1] % mod;
}
invf[N - 1] = qpow(fac[N - 1], mod - 2);
for (int i = N - 2; i >= 0; i--) {
invf[i] = invf[i + 1] * (i + 1) % mod;
}
}
int pre[N], suf[N];
int cal(int* a, int n, int k) {
pre[0] = k; suf[n + 1] = 1;
for (int i = 1; i <= n; i++)pre[i] = pre[i - 1] * (k - i) % mod;
for (int i = n; i >= 0; i--)suf[i] = suf[i + 1] * (k - i) % mod;
int ans = 0;
for (int i = 0; i <= n; i++) {
int f = invf[n - i] * invf[i] % mod;
if ((n - i) & 1)f = -f;
ans = (ans + a[i] * f % mod * (i == 0 ? 1 : pre[i - 1]) % mod * suf[i + 1]) % mod;
if (ans < 0) ans += mod;
}
return ans;
}
int T, n, m;
signed main() {
init();
scanf("%lld", &T);
while (T--) {
scanf("%lld%lld", &n, &m);
for (int i = 0; i <= n; i++) {
scanf("%lld", y + i); if (i > 0) S[i] = (S[i - 1] + y[i]) % mod; else S[i] = y[i];
}
y[n + 1] = cal(y, n, n + 1);
S[n + 1] = (S[n] + y[n + 1]) % mod;
while (m--) {
int l, r;
scanf("%lld%lld", &l, &r);
int ans = cal(S, n + 1, r) - cal(S, n + 1, l - 1);
if (ans < 0)ans += mod;
printf("%lld\n", ans % mod);
}
}
}
/*
1
3 2
1 10 49 142
6 7
95000 100000
*/
5.10 高斯消元
解多元一次方程组
/*
* @Author: zhl
* @Date: 2020-11-14 09:22:58
*/
#include<bits/stdc++.h>
using namespace std;
int n;
struct Gauss {
double a[110][110];
int n;
int solve() {
for (int i = 1; i <= n; i++) {
int mx = i;
for (int j = i + 1; j <= n; j++) {
if (fabs(a[j][i]) > fabs(a[mx][i])) mx = j;
}
for (int j = 1; j <= n + 1; j++)swap(a[i][j], a[mx][j]);
if (fabs(a[i][i]) < 1e-8) {
puts("No Solution");
return -1;
}
for (int j = 1; j <= n; j++) {
if (i == j)continue;
double t = a[j][i] / a[i][i];
for (int k = i + 1; k <= n + 1; k++) {
a[j][k] -= a[i][k] * t;
}
}
}
for (int i = 1; i <= n; i++) {
a[i][n + 1] /= a[i][i];
a[i][i] = 1.0;
}
}
}G;
int main() {
scanf("%d", &n);G.n = n;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n + 1; j++) {
scanf("%lf", &G.a[i][j]);
}
}
if (G.solve() != -1){
for (int i = 1;i <= n;i++) {
printf("%.2f\n", G.a[i][n + 1]);
}
}
}
5.11 卢卡斯
( 不是卢斯卡...
求组合数模数的方法
\[C_m^n = \dfrac {m!} {n!(m-n)!}
\]
一般情况下对一个大素数 \(p\) 取模， 可以线性处理出阶乘，阶乘的逆元， \(O(1)\) 计算就可以。
const int N = 1e6 + 10;
int fac[N],invfac[N],inv[N];
const int mod = 998244353;
void init(){
fac[0] = invfac[0] = 1;
fac[1] = invfac[1] = 1;
inv[1] = 1;
for(int i = 2;i < N;i++){
fac[i] = fac[i-1] * i % mod;
inv[i] = (mod - mod / i)*inv[mod % i] % mod;
invfac[i] = invfac[i-1] * inv[i] % mod;
}
}
int C(int n,int m){
return fac[n]*invfac[n-m]*invfac[m];
}
但是， 当 \(p < m\) 的时候，就需要用 \(Lucas\) 了
\[C_m^n = C_{m\%p}^{n\%p} \cdot \ C_{m/p}^{n/p} \ \ (mod\ \ p)
\]
/*
* @Author: zhl
* @Date: 2020-11-12 10:27:57
*/
#include<bits/stdc++.h>
using ll = long long;
using namespace std;
const int N = 1e6 + 10;
ll fac[N], invfac[N], inv[N];
void init(int n, int mod) {
fac[0] = invfac[0] = 1;
fac[1] = invfac[1] = 1;
inv[1] = 1;
for (int i = 2; i < n; i++) {
fac[i] = fac[i - 1] * i % mod;
inv[i] = (mod - mod / i) * inv[mod % i] % mod;
invfac[i] = invfac[i - 1] * inv[i] % mod;
}
}
// 需要先预处理出fact[]，即阶乘
ll C(ll m, ll n, ll p){
return m < n ? 0 : fac[m] * invfac[n] % p * invfac[m - n] % p;
}
ll lucas(ll m, ll n, ll p){
return n == 0 ? 1 % p : lucas(m / p, n / p, p) * C(m % p, n % p, p) % p;
}
int T, n, m, k;
int main() {
scanf("%d", &T);
while (T--) {
scanf("%d%d%d", &n, &m, &k);
init(n + m + 1, k);
printf("%lld\n", lucas(n + m, n, k));
}
}
六、数据结构
6.1 线段树
区间修改区间查询
/*
* @Author: zhl
* @LastEditTime: 2020-12-08 19:35:36
*/
#include<bits/stdc++.h>
#define lo (o<<1)
#define ro (o<<1|1)
#define mid (l+r>>1)
using namespace std;
using ll = long long;
const int N = 1e5 + 10;
ll sum[N << 2], lz[N << 2], A[N];
int n, q;
void build(int o = 1, int l = 1, int r = n) {
if (l == r) {
sum[o] = A[l];
return;
}
build(lo, l, mid);build(ro, mid + 1, r);
sum[o] = sum[lo] + sum[ro];
}
void push_down(int o, int l, int r) {
if (lz[o] == 0)return;
lz[lo] += lz[o], lz[ro] += lz[o];
sum[lo] += lz[o] * (mid - l + 1);
sum[ro] += lz[o] * (r - mid);
lz[o] = 0;
}
void updt(int L, int R, ll val, int o = 1, int l = 1, int r = n) {
if (L <= l and r <= R) {
lz[o] += val;
sum[o] += val * (r - l + 1);
return;
}
push_down(o, l, r);
if (L <= mid)updt(L, R, val, lo, l, mid);
if (R > mid)updt(L, R, val, ro, mid + 1, r);
sum[o] = sum[lo] + sum[ro];
}
ll query(int L, int R, int o = 1, int l = 1, int r = n) {
if (L <= l and r <= R) {
return sum[o];
}
ll ans = 0;
push_down(o, l, r);
if (L <= mid)ans += query(L, R, lo, l, mid);
if (R > mid) ans += query(L, R, ro, mid + 1, r);
return ans;
}
int main() {
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
#endif
scanf("%d%d", &n, &q);
for (int i = 1;i <= n;i++)scanf("%d", A + i);
build();
while (q--) {
int op, a, b, c;
scanf("%d", &op);
if (op == 1) {
scanf("%d%d%d", &a, &b, &c);
updt(a, b, c);
}
else {
scanf("%d%d", &a, &b);
printf("%lld\n", query(a, b));
}
}
}
扫描线
经典应用，求矩形面积的并
注意下标的差别
区间[l, r] 对应的横坐标分别是 x[l] 和 x[r + 1]
#include<bits/stdc++.h>
#define mid (l+r>>1)
#define lo (o<<1)
#define ro (o<<1|1)
using namespace std;
typedef long long ll;
const int N = 4e5 + 10;
int n;
int nums[N], cnt;
struct line {
int l, r, h, tag;
bool operator < (const line& b)const {
return h < b.h;
}
}L[N << 1];
ll len[N << 2], times[N << 2];
void push_up(int o, int l, int r) {
if (times[o])len[o] = nums[r + 1] - nums[l];
else len[o] = len[lo] + len[ro];
}
void updt(int L, int R, int val, int o = 1, int l = 1, int r = cnt - 1) {
if (nums[r + 1] <= L or R <= nums[l])return;
if (L <= nums[l] and nums[r + 1] <= R) {
times[o] += val;
push_up(o, l, r);
return;
}
updt(L, R, val, lo, l, mid);
updt(L, R, val, ro, mid + 1, r);
push_up(o, l, r);
}
int main() {
#ifdef ONLINE_JUDGE
#else
freopen("in.txt", "r", stdin);
#endif
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
int lx, ly, rx, ry;
scanf("%d%d%d%d", &lx, &ly, &rx, &ry);
nums[++cnt] = lx, nums[++cnt] = rx;
L[(i << 1) - 1] = { lx,rx,ly,1 };
L[i << 1] = { lx,rx,ry,-1 };
}
sort(L + 1, L + 1 + 2 * n);
sort(nums + 1, nums + 1 + cnt);
cnt = unique(nums + 1, nums + 1 + cnt) - nums - 1;
ll ans = 0;
for (int i = 1; i <= 2 * n - 1; i++) {
updt(L[i].l, L[i].r, L[i].tag);
ans += len[1] * (L[i + 1].h - L[i].h);
}
printf("%lld\n", ans);
}
6.2 树状数组
单点修改，区间查询
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
int C[N], n, q, x;
void add(int p, int v) {
for (; p <= n; p += -p & p)C[p] += v;
}
ll query(int p) {
ll ans = 0;
for (; p; p -= -p & p)ans += C[p];
return ans;
}
int main() {
scanf("%d%d", &n, &q);
for (int i = 1; i <= n; i++)scanf("%d", &x), add(i, x);
while (q--) {
int op, a, b; scanf("%d%d%d", &op, &a, &b);
if (op == 1)add(a, b);
else printf("%lld\n", query(b) - query(a - 1));
}
}
区间修改，区间查询
设 \(A_i\) 是原数组， \(d_i = A_i - A_{i-1}\) 是 \(A\) 的差分数组
有
\[S_n = \sum_{i=1}^nA_i = d_1 + \\d_1 + d_2 +\\ d_1 + d_2 + d_3 + \\ ... \\d_1 + d_2 + d_3 + d_4 + ... + d_n \\ = n (d_1 + d_2 + ... + d_n) - \sum_{i=1}^nd_i(i-1)
\]
设 \(B_i = d_i(i-1)\)
则
\[S_n = n\sum d - \sum B
\]
而当一段区间 \([L,R]\) 一起加上 \(x\) 的时候，
对于 \(d\) 来说，只有 \(d_L\) 和 \(d_{R+1}\) 发生了变化
对于 \(B\) 来说，也是同理，所以可以开两个树状数组来进行维护
/*
* @Author: zhl
* @Date: 2020-11-17 10:33:57
*/
#include<bits/stdc++.h>
using ll = long long;
using namespace std;
const int N = 1e5 + 10;
int n, m;
struct{
ll C[N][2]; // 0 是差分d_i , 1 是 d_i * (i - 1)
void add(int pos, ll val, int o) {
for (; pos <= n; pos += (-pos) & pos) C[pos][o] += val;
}
ll ask(int pos, int o) {
ll ans = 0;
for (; pos; pos -= (-pos) & pos) ans += C[pos][o];
return ans;
}
void updt(int l, int r, int x) {
add(l, x, 0); add(r + 1, -x, 0);
add(l, x * (l - 1), 1); add(r + 1, -x * (r), 1);
}
ll query(int l, int r) {
ll R = r * ask(r, 0) - ask(r, 1);
ll L = (l - 1) * ask(l - 1, 0) - ask(l - 1, 1);
return R - L;
}
}BIT;
int main() {
scanf("%d%d", &n, &m);
int pre = 0;
for (int i = 1; i <= n; i++) {
int x; scanf("%d", &x);
BIT.add(i,x - pre,0);
BIT.add(i, 1ll * (x - pre)* (i - 1), 1);
pre = x;
}
while (m--) {
int op, a, b, x;
scanf("%d", &op);
if (op == 1) {
scanf("%d%d%d", &a, &b, &x);
BIT.updt(a, b, x);
}
else {
scanf("%d%d", &a, &b);
printf("%lld\n", BIT.query(a, b));
}
}
}
6.3 主席树
也叫可持久化线段树，这里线段树用做了桶。
这个是单点增加，其实就是把一条链挂在另一条链上
复制信息，然后开点
这里是线性的挂链，也可以挂成树形。
#include<bits/stdc++.h>
#define mid (l+r>>1)
using namespace std;
const int maxn = 5e5 + 10;
int sum[maxn << 5], L[maxn << 5], R[maxn << 5];
int cnt;
int a[maxn], id[maxn], root[maxn];
int build(int l, int r) {
int rt = ++cnt;
sum[rt] = 0;
if (l < r) {
L[rt] = build(l, mid);
R[rt] = build(mid + 1, r);
}
return rt;
}
int updt(int pre, int l, int r, int pos) {
int rt = ++cnt;
sum[rt] = sum[pre] + 1;
R[rt] = R[pre];
L[rt] = L[pre];
if (l < r) {
if (pos <= mid) {
L[rt] = updt(L[pre], l, mid, pos);
}
else {
R[rt] = updt(R[pre], mid + 1, r, pos);
}
}
return rt;
}
int query(int x, int y, int l, int r, int k) {
if (l == r) {
return r;
}
int num = sum[L[y]] - sum[L[x]];
if (num >= k) {
return query(L[x], L[y], l, mid, k);
}
else {
return query(R[x], R[y], mid + 1, r, k - num);
}
}
int T, n, m;
int main() {
//scanf("%d", &T);
T = 1;
while (T--) {
scanf("%d%d", &n, &m);
cnt = 0;
for (int i = 1; i <= n; i++) {
scanf("%d", a + i);
id[i] = a[i];
}
sort(id + 1, id + n + 1);
int cntID = unique(id + 1, id + n + 1) - (id + 1);
root[0] = build(1, cntID);
for (int i = 1; i <= n; i++) {
int pos = lower_bound(id + 1, id + cntID + 1, a[i]) - id;
root[i] = updt(root[i - 1], 1, cntID, pos);
}
for (int i = 1; i <= m; i++) {
int x, y, k;
scanf("%d%d%d", &x, &y, &k);
int ind = query(root[x - 1], root[y], 1, cntID, k);
printf("%d\n", id[ind]);
}
}
}
6.4 01Tire树
按二进制来把一个数挂到树上对应的链，来求解一些二进制问题
\(01Tire\) 可以用来解决 \(xor\) 问题
struct{
int c[N][2],tot;
int getnode(){
tot++;
c[tot][0] = c[tot][1] = 0;
return tot;
}
void insert(int val){
int u = 0;
for(int i = maxbit;i >= 0;i--){
int v = (val & (1 << i) ) ? 1 : 0;
if(!c[u][v])c[u][v] = getnode();
u = c[u][v];
}
}
void init(){
c[0][0] = c[0][1] = 0;
tot = 0;
}
}Tire;
动态开点
int getnode(){
tot++;
c[tot][0] = c[tot][1] = 0;
return tot;
}
动态开点的好处就是在多数数据的时候不需要 memset
数据插入
void insert(int val){
int u = 0;
for(int i = maxbit;i >= 0;i--){
int v = (val & (1 << i) ) ? 1 : 0;
if(!c[u][v])c[u][v] = getnode();
u = c[u][v];
}
}
从高位到低位插入到01字典树中
01Tire
给一个集合，每次询问给出 \(x\) ,输出集合中的数 \(k\) 使得它们异或最大。
注意是输出数，不是输出最大的异或值
思路:
用集合里的数建 \(01Tire\) ，将 \(x\) 按位取反，从高位开始匹配，匹配失败则换一边
#include<bits/stdc++.h>
using namespace std;
const int N = 2e6 + 10;
const int maxbit = 30; //int不能开31,intmax = (1<<31)-1
struct{
int c[N][2],tot;
int getnode(){
tot++;
c[tot][0] = c[tot][1] = 0;
return tot;
}
void insert(int val){
int u = 0;
for(int i = maxbit;i >= 0;i--){
int v = (val & (1 << i) ) ? 1 : 0;
if(!c[u][v])c[u][v] = getnode();
u = c[u][v];
}
}
int query(int val){
int u = 0;
int ans = 0;
for(int i = maxbit;i >= 0;i--){
int v = (val & (1 << i)) ? 0 : 1;
if(!c[u][v]) v ^= 1;
if(v)ans += (1 << i);
u = c[u][v];
}
return ans;
}
void init(){
c[0][0] = c[0][1] = 0;
tot = 0;
}
}Tire;
int n,m,x,T;
int main(){
scanf("%d",&T);
for(int c = 1;c <= T;c++){
Tire.init();
scanf("%d%d",&n,&m);
for(int i = 0;i < n;i++){
scanf("%d",&x);
Tire.insert(x);
}
printf("Case #%d:\n",c);
for(int i = 0;i < m;i++){
scanf("%d",&x);
printf("%d\n",Tire.query(x));
}
}
}
可持久化Tire
区间查询
搞一个可持久化的Tire就好了
插入：
// root[i] = insert(root[i-1],v,val);
int insert(int pre, int v, int val) {
int u = getnode();
int ans = u;
for (int i = maxbit; i >= 0; i--) {
c[u][0] = c[pre][0];
c[u][1] = c[pre][1]; //复制信息
int x = val & (1 << i) ? 1 : 0;
c[u][x] = getnode();//开点
u = c[u][x]; // 0 是空的节点，所以可以一直这样迭代
pre = c[pre][x];
}
return ans;
}
其实也很简单，就是复制之前的信息，然后开点。
查询:
由于开点是一个一个分配的，所以只要 id < root[l] 就不是区间内
，所以只要加上这一个判断就跟之前的一样。
int query(int l, int r, int x) {
int MinID = root[l];
int u = root[r];
int ans = 0;
for (int i = maxbit; i >= 0; i--) {
int now = (x & (1 << i)) ? 0 : 1;
if (c[u][now] and c[u][now] >= MinID) {
u = c[u][now];
ans += (1 << i);
}
else {
u = c[u][now ^ 1];
}
}
return ans;
}
完整代码
/*
* @Author: zhl
* @Date: 2020-10-13 09:46:47
*/
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i = a;i <= b;i++)
#define repE(i,u) for(int i = head[u];i;i = E[i].next)
#define swap(a,b) a^=b,b^=a,a^=b
const int N = 2e6 + 10;
const int maxbit = 30;
struct {
int root[N], c[N][2], tot;
void init() {
c[0][0] = c[0][1] = 0;
tot = 0;
root[0] = 0;
}
int getnode() {
tot++;
c[tot][0] = c[tot][1] = 0;
return tot;
}
//root[v] = insret(Tire.root[v-1], v, val);
int insert(int pre, int v, int val) {
int u = getnode();
int ans = u;
for (int i = maxbit; i >= 0; i--) {
c[u][0] = c[pre][0];
c[u][1] = c[pre][1];
int x = val & (1 << i) ? 1 : 0;
c[u][x] = getnode();
u = c[u][x];
pre = c[pre][x];
}
return ans;
}
int query(int l, int r, int x) {
int Treesize = maxbit + 2;
int MinID = root[l];
int u = root[r];
int ans = 0;
for (int i = maxbit; i >= 0; i--) {
int now = (x & (1 << i)) ? 0 : 1;
if (c[u][now] and c[u][now] >= MinID) {
u = c[u][now];
ans += (1 << i);
}
else {
u = c[u][now ^ 1];
}
}
return ans;
}
}Tire;
int n, m, l, r, x;
int A[N];
int main() {
scanf("%d%d", &n, &m);
Tire.init();
for (int i = 1; i <= n; i++) {
scanf("%d", A + i);
Tire.root[i] = Tire.insert(Tire.root[i-1],i,A[i]);
}
for (int i = 1; i <= m; i++) {
scanf("%d%d%d", &x, &l, &r);
printf("%d\n", Tire.query(l + 1, r + 1, x));
}
}
6.5 Treap
Tree + Heap
\(Treap\) 是平衡树的一种，\(Treap\) 是 \(Tree\) 和 \(Heap\) 的组合
核心思想
每个节点有两个属性 \(key\) ， \(val\) 其中的 key 满足 BST 二叉搜索树的性质，其中序遍历是一个有序序列。val 满足 Heap 堆的性质，一个节点的 \(val\) 值大于其孩子节点的 \(val\)
随机分配 \(val\) 使得 期望的 \(BST\) 是平均深度的
结构定义
struct Node{
int l, r;
int key, val;//key是BST关键字， val是Heap关键字
int cnt, size;
}tr[N];
int root, idx;
节点分配
int get_node(int key){
tr[ ++ idx].key = key;
tr[idx].val = rand(); //随机数据
tr[idx].cnt = tr[idx].size = 1;
return idx;
}
插入操作
void insert(int &p, int key)
{
if (!p) p = get_node(key);
else if (tr[p].key == key) tr[p].cnt ++ ;
else if (tr[p].key > key)
{
insert(tr[p].l, key);
if (tr[tr[p].l].val > tr[p].val) zig(p);//右旋
}
else
{
insert(tr[p].r, key);
if (tr[tr[p].r].val > tr[p].val) zag(p);//左旋
}
pushup(p);
}
删除操作
void remove(int &p, int key)
{
if (!p) return;
if (tr[p].key == key)
{
if (tr[p].cnt > 1) tr[p].cnt -- ;
else if (tr[p].l || tr[p].r)
{
if (!tr[p].r || tr[tr[p].l].val > tr[tr[p].r].val)
{
zig(p);
remove(tr[p].r, key);
}
else
{
zag(p);
remove(tr[p].l, key);
}
}
else p = 0;
}
else if (tr[p].key > key) remove(tr[p].l, key);
else remove(tr[p].r, key);
pushup(p);
}
旋转操作
void zig(int &p) // 右旋
{
int q = tr[p].l;
tr[p].l = tr[q].r, tr[q].r = p, p = q;
pushup(tr[p].r), pushup(p);
}
void zag(int &p) // 左旋
{
int q = tr[p].r;
tr[p].r = tr[q].l, tr[q].l = p, p = q;
pushup(tr[p].l), pushup(p);
}
模板
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010, INF = 1e8;
int n;
struct Node
{
int l, r;
int key, val;//key是BST关键字， val是Heap关键字
int cnt, size;
}tr[N];
int root, idx;
void pushup(int p)
{
tr[p].size = tr[tr[p].l].size + tr[tr[p].r].size + tr[p].cnt;
}
int get_node(int key)
{
tr[ ++ idx].key = key;
tr[idx].val = rand(); //随机数据
tr[idx].cnt = tr[idx].size = 1;
return idx;
}
void zig(int &p) // 右旋
{
int q = tr[p].l;
tr[p].l = tr[q].r, tr[q].r = p, p = q;
pushup(tr[p].r), pushup(p);
}
void zag(int &p) // 左旋
{
int q = tr[p].r;
tr[p].r = tr[q].l, tr[q].l = p, p = q;
pushup(tr[p].l), pushup(p);
}
void build()
{
get_node(-INF), get_node(INF);
root = 1, tr[1].r = 2;
pushup(root);
if (tr[1].val < tr[2].val) zag(root);
}
void insert(int &p, int key)
{
if (!p) p = get_node(key);
else if (tr[p].key == key) tr[p].cnt ++ ;
else if (tr[p].key > key)
{
insert(tr[p].l, key);
if (tr[tr[p].l].val > tr[p].val) zig(p);
}
else
{
insert(tr[p].r, key);
if (tr[tr[p].r].val > tr[p].val) zag(p);
}
pushup(p);
}
void remove(int &p, int key)
{
if (!p) return;
if (tr[p].key == key)
{
if (tr[p].cnt > 1) tr[p].cnt -- ;
else if (tr[p].l || tr[p].r)
{
if (!tr[p].r || tr[tr[p].l].val > tr[tr[p].r].val)
{
zig(p);
remove(tr[p].r, key);
}
else
{
zag(p);
remove(tr[p].l, key);
}
}
else p = 0;
}
else if (tr[p].key > key) remove(tr[p].l, key);
else remove(tr[p].r, key);
pushup(p);
}
int get_rank_by_key(int p, int key) // 通过数值找排名
{
if (!p) return 0; // 本题中不会发生此情况
if (tr[p].key == key) return tr[tr[p].l].size + 1;
if (tr[p].key > key) return get_rank_by_key(tr[p].l, key);
return tr[tr[p].l].size + tr[p].cnt + get_rank_by_key(tr[p].r, key);
}
int get_key_by_rank(int p, int rank) // 通过排名找数值
{
if (!p) return INF; // 本题中不会发生此情况
if (tr[tr[p].l].size >= rank) return get_key_by_rank(tr[p].l, rank);
if (tr[tr[p].l].size + tr[p].cnt >= rank) return tr[p].key;
return get_key_by_rank(tr[p].r, rank - tr[tr[p].l].size - tr[p].cnt);
}
int get_prev(int p, int key) // 找到严格小于key的最大数
{
if (!p) return -INF;
if (tr[p].key >= key) return get_prev(tr[p].l, key);
return max(tr[p].key, get_prev(tr[p].r, key));
}
int get_next(int p, int key) // 找到严格大于key的最小数
{
if (!p) return INF;
if (tr[p].key <= key) return get_next(tr[p].r, key);
return min(tr[p].key, get_next(tr[p].l, key));
}
int main()
{
build();
scanf("%d", &n);
while (n -- )
{
int opt, x;
scanf("%d%d", &opt, &x);
if (opt == 1) insert(root, x);
else if (opt == 2) remove(root, x);
else if (opt == 3) printf("%d\n", get_rank_by_key(root, x) - 1);
else if (opt == 4) printf("%d\n", get_key_by_rank(root, x + 1));
else if (opt == 5) printf("%d\n", get_prev(root, x));
else printf("%d\n", get_next(root, x));
}
return 0;
}
6.6 Splay
Splay 是平衡树
\(Splay\) 是平衡树的一种
基本思想是， 对于查找频率较高的节点，使其处于离根节点相对较近的节点。
Spaly的基本操作有
- rotate（旋转）
- splay （伸展）
- push_up
- push_down
struct Node {
int son[2], fa, val;
int size, flag;
void init(int _val, int _fa) {
val = _val; fa = _fa;
size = 1;
}
}tr[N];
rotate()
这个旋转操作跟数据结构里学的平衡树旋转操作是一样的。
如下图，画的是右旋 \(x\) 的操作，蓝色的边表示信息发生了改变
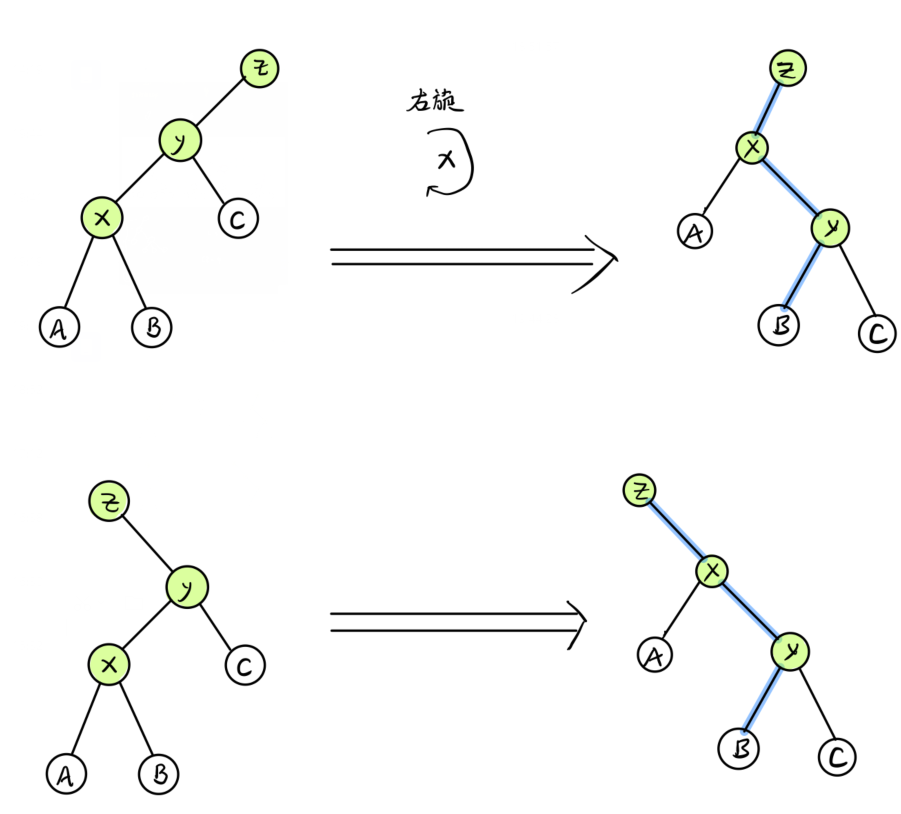
void rotate(int x) {
int y = tr[x].fa, z = tr[y].fa;
int k = (tr[y].son[1] == x); // k = 0 表示 x 是 y 的左儿子
tr[z].son[tr[z].son[1] == y] = x, tr[x].fa = z;
tr[y].son[k] = tr[x].son[k ^ 1], tr[tr[x].son[k ^ 1]].fa = y;
tr[x].son[k ^ 1] = y, tr[y].fa = x;
push_up(y), push_up(x);
}
代码中修改信息的三行对应了三条蓝边，上图表示的情况是 \(k=0\)
splay()
接口 splay(int x,int k) 把节点 \(u\) 转到 \(k\) 下面，若 \(k\) 为 \(0\) , 则转到根的位置
void splay(int x, int k) {
while (tr[x].fa != k) {
int y = tr[x].fa, z = tr[y].fa;
if (z != k) {
if ((tr[y].son[1] == x) ^ (tr[z].son[1] == y))rotate(x);
else rotate(y); //转y才是log复杂度
}
rotate(x);
}
if (!k)root = x;
}
if ((tr[y].son[1] == x) ^ (tr[z].son[1] == y)) 表示的是不是链状，此时转两下 \(x\) ,若是链状，则需要先转一下 \(y\) 再转 \(x\) ，不能转两次 \(x\)
push_up()
类似线段树的 push_up() ，一般只需要维护 \(size\)
void push_up(int u) {
tr[u].size = tr[tr[u].son[0]].size + tr[tr[u].son[1]].size + 1;
}
push_down()
在需要 \(lazytag\) 时将标记下传
洛谷模板
区间翻转
/*
* @Author: zhl
* @Date: 2020-11-06 14:24:16
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, m;;
struct Node {
int son[2], fa, val;
int size, flag;
void init(int _val, int _fa) {
val = _val; fa = _fa;
size = 1;
}
}tr[N];
int root, idx;
void push_up(int u) {
tr[u].size = tr[tr[u].son[0]].size + tr[tr[u].son[1]].size + 1;
}
void push_donw(int u) {
if (tr[u].flag) {
swap(tr[u].son[0], tr[u].son[1]);
tr[tr[u].son[0]].flag ^= 1;
tr[tr[u].son[1]].flag ^= 1;
tr[u].flag = 0;
}
}
void rotate(int x) {
int y = tr[x].fa, z = tr[y].fa;
int k = (tr[y].son[1] == x); // k = 0 表示 x 是 y 的左儿子
tr[z].son[tr[z].son[1] == y] = x, tr[x].fa = z;
tr[y].son[k] = tr[x].son[k ^ 1], tr[tr[x].son[k ^ 1]].fa = y;
tr[x].son[k ^ 1] = y, tr[y].fa = x;
push_up(y), push_up(x);
}
void splay(int x, int k) {
while (tr[x].fa != k) {
int y = tr[x].fa, z = tr[y].fa;
if (z != k) {
if ((tr[y].son[1] == x) ^ (tr[z].son[1] == y))rotate(x);
else rotate(y); //
}
rotate(x);
}
if (!k)root = x;
}
void insert(int val) {
int u = root, p = 0;
while (u) p = u, u = tr[u].son[val > tr[u].val];
u = ++idx;
if (p) tr[p].son[val > tr[p].val] = u;
tr[u].init(val, p);
splay(u, 0);
}
int get_k(int k) {
int u = root;
while (1) {
push_donw(u);
if (tr[tr[u].son[0]].size >= k) u = tr[u].son[0];
else if (tr[tr[u].son[0]].size + 1 == k)return u;
else k -= tr[tr[u].son[0]].size + 1, u = tr[u].son[1];
}
}
void output(int u) {
push_donw(u);
if (tr[u].son[0]) output(tr[u].son[0]);
if (tr[u].val >= 1 and tr[u].val <= n)printf("%d ", tr[u].val);
if (tr[u].son[1]) output(tr[u].son[1]);
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 0; i <= n + 1; i++)insert(i);
while (m--) {
int l, r;
scanf("%d%d", &l, &r);
l = get_k(l), r = get_k(r + 2);
splay(l, 0); splay(r, l);
tr[tr[r].son[0]].flag ^= 1;
}
output(root);
}
永无乡
启发式合并
/*
* @Author: zhl
* @Date: 2020-11-11 15:27:48
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
struct Node {
int v, s[2], p, id, size;
void init(int _v, int _id, int _p) {
v = _v; id = _id; p = _p; size = 1;
}
}tr[N];
int idx, root[N];
int n, m;
int fa[N];
int find(int a) {
return a == fa[a] ? a : fa[a] = find(fa[a]);
}
void push_up(int x) {
tr[x].size = tr[tr[x].s[0]].size + tr[tr[x].s[1]].size + 1;
}
void rotate(int x) {
int y = tr[x].p, z = tr[y].p;
int k = tr[y].s[1] == x;
tr[z].s[tr[z].s[1] == y] = x; tr[x].p = z;
tr[y].s[k] = tr[x].s[k ^ 1]; tr[tr[x].s[k ^ 1]].p = y;
tr[x].s[k ^ 1] = y; tr[y].p = x;
push_up(y), push_up(x);
}
void splay(int x, int k, int rt) {
while (tr[x].p != k) {
int y = tr[x].p, z = tr[y].p;
if (z != k) {
if ((tr[z].s[0] == y) ^ (tr[y].s[0] == x))rotate(x);
else rotate(y);
}
rotate(x);
}
if (!k)root[rt] = x;
}
void insert(int v, int id, int rt) {
int u = root[rt], p = 0;
while (u) p = u, u = tr[u].s[v > tr[u].v];
u = ++idx;
if (p)tr[p].s[v > tr[p].v] = u;
tr[u].init(v, id, p);
splay(u, 0, rt);
}
int get_k(int k, int rt) {
int u = root[rt];
while (u) {
if (tr[tr[u].s[0]].size >= k) u = tr[u].s[0];
else if (tr[tr[u].s[0]].size + 1 == k)return tr[u].id;
else k -= tr[tr[u].s[0]].size + 1, u = tr[u].s[1];
}
return -1;
}
void dfs(int a, int b) {
if (tr[a].s[0])dfs(tr[a].s[0], b);
if (tr[a].s[1])dfs(tr[a].s[1], b);
insert(tr[a].v, tr[a].id, b);
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
fa[i] = root[i] = i;
int v; scanf("%d", &v);
tr[i].init(v, i, 0);
}
idx = n;
for (int i = 1; i <= m; i++) {
int a, b; scanf("%d%d", &a, &b);
a = find(a); b = find(b);
if (a != b) {
if (tr[root[a]].size > tr[root[b]].size)swap(a, b);
dfs(root[a], b);
fa[a] = b;
}
}
scanf("%d", &m);
while (m--) {
char op[2]; int a, b;
scanf("%s%d%d", op, &a, &b);
if (*op == 'B') {
a = find(a); b = find(b);
if (a != b) {
if (tr[root[a]].size > tr[root[b]].size)swap(a, b);
dfs(root[a],b);
fa[a] = b;
}
}
else {
a = find(a);
if (tr[root[a]].size < b)puts("-1");
else {
printf("%d\n", get_k(b, a));
}
}
}
}
6.7 块状链表
对于线性表，可以 \(O(1)\) 的访问，但是插入和删除操作是 \(O(n)\)
对于链表，可以 \(O(1)\) 的进行插入和删除，但是是 \(O(n)\) 的访问。
于是本着分块的思想，有了块状链表 。
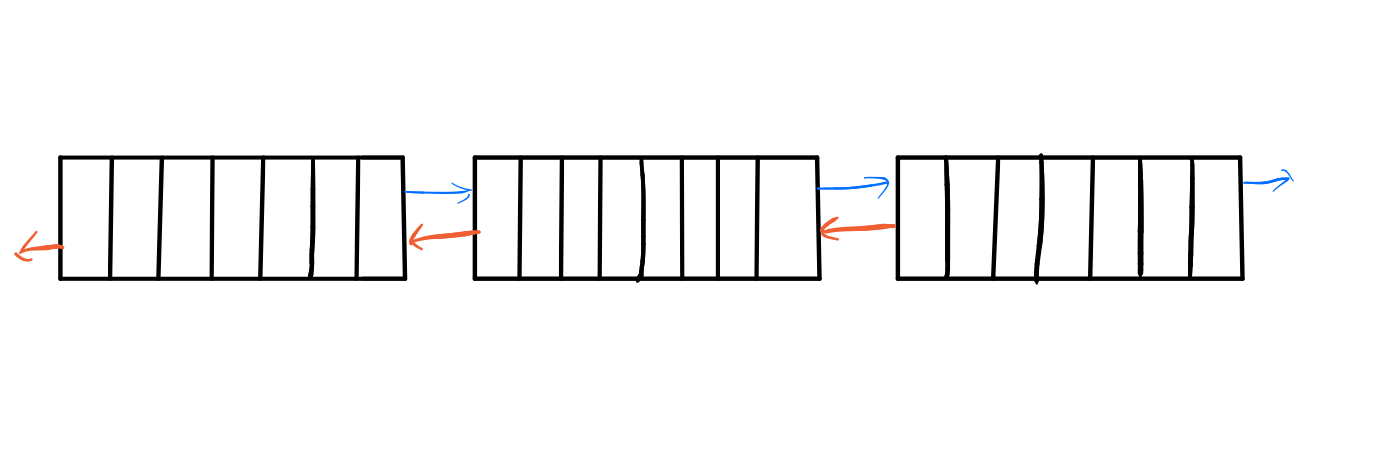
大概长这个样子。每个块的大小数量级在 \(O(\sqrt n)\) , 块数的量级 \(O(\sqrt n)\)
主要有以下几种操作：
插入
（1） 分裂节点 \(O(\sqrt n)\)
（2） 在分裂点插入 \(O(\sqrt n)\)
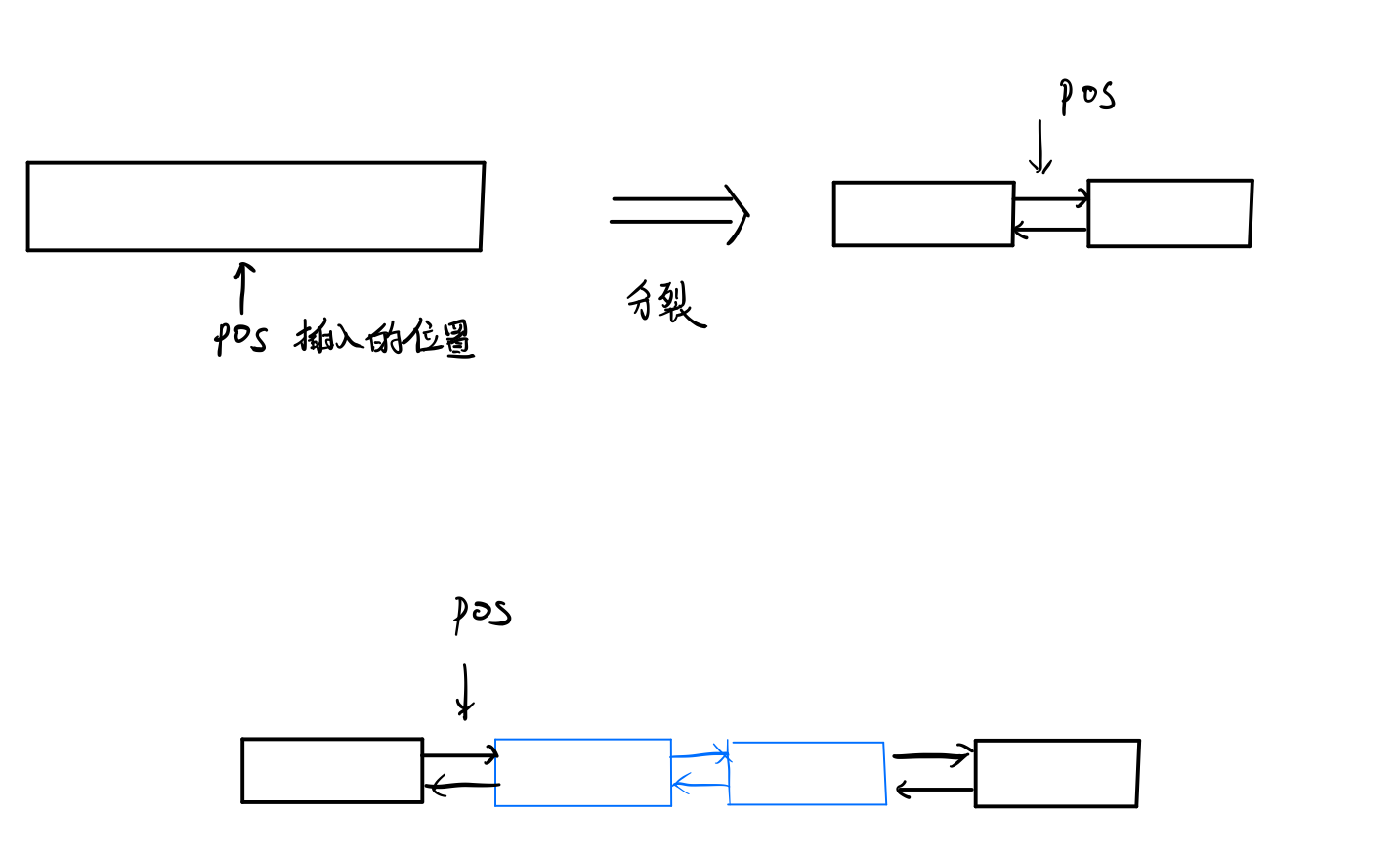
删除
（1） 删除开头节点的后半部分 \(O(\sqrt n)\)
（2） 删除中心完整节点 \(O(\sqrt n)\)
（3） 删除结尾节点的前半部分 \(O(\sqrt n)\)
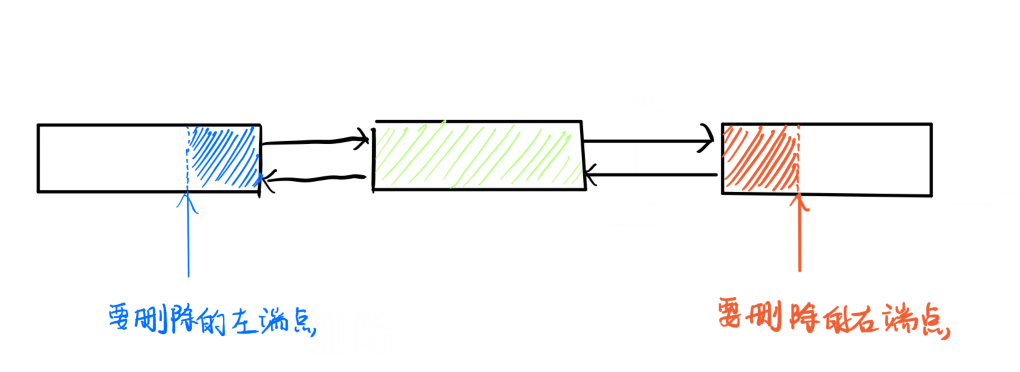
合并
为了保证正确的复杂度，要不定期的进行合并操作。
所谓合并操作，就是从第一个块开始，如果把下一个块合并过来之后大小不大于 $ \sqrt n$ ，就把两个块合并
若没有合并操作，则可能会有很多小块，导致 \(TLE\)
rope
STL 中带的块状链表，内部好像是平衡树实现的
【2020牛客国庆派对Day8】 G. Shuffle Cards
题意：
给 \(n,m\)
初始状态为 \(1,2,3,...,n\)
\(m\) 次操作，每次操作从 \(pos\) 出开始，取 \(l\) 长度，把这一段取出放到最前面
问最后的状态
#include <bits/stdc++.h>
#include <ext/rope>
using namespace std;
using namespace __gnu_cxx;
const int N = 100010;
int main() {
int n, m, a[N] = {0}; cin >> n >> m;
for (int i = 0; i < n; i++) a[i] = i + 1;
rope<int> rp(a);
while (m--) {
int p, s; cin >> p >> s; p--;
rp.insert(0, rp.substr(p, s));
rp.erase(p + s, s);
}
for (auto i : rp) cout << i << " ";
return 0;
}
代码
/*
* @Author: zhl
* @Date: 2020-11-18 11:30:27
*/
#include<bits/stdc++.h>
#pragma GCC optimize(2)
using namespace std;
const int N = 2e3 + 10, M = 2e3 + 10;
struct node {
char s[N + 1];
int c, l, r;
}p[M];
int id[N], idx;//可分配的编号池
char str[2000010];
int n, x, y;
void move(int k)//移动到第k个字符后面
{
x = p[0].r;
while (k > p[x].c) k -= p[x].c, x = p[x].r;
y = k - 1;
}
void add(int x, int u) //将节点u插到节点x的右边
{
p[u].r = p[x].r; p[p[u].r].l = u;
p[x].r = u; p[u].l = x;
}
void del(int u) //删除节点u
{
p[p[u].l].r = p[u].r;
p[p[u].r].l = p[u].l;
p[u].l = p[u].r = p[u].c = 0;
id[++idx] = u;
}
void insert(int k) //在光标后面插入k个字符
{
if (y + 1 != p[x].c) //分裂
{
int u = id[idx--];
for (int i = y + 1; i < p[x].c; i++) p[u].s[p[u].c++] = p[x].s[i];
p[x].c = y + 1;
add(x, u);
}
int cur = x, i = 0;
while (i < k) {
int u = id[idx--];
for (; i < k and p[u].c < N; i++) {
p[u].s[p[u].c++] = str[i];
}
add(cur, u);
cur = u;
}
}
void remove(int k) //删除光标后的k个字符
{
if (y + 1 + k <= p[x].c) {
for (int i = y + 1, j = y + 1 + k; j < p[x].c; j++,i++) {
p[x].s[i] = p[x].s[j];
}
p[x].c -= k;
}
else {
k -= (p[x].c - y - 1);
p[x].c = y + 1;
while (p[x].r and k >= p[p[x].r].c) {
k -= p[p[x].r].c;
del(p[x].r);
}
int u = p[x].r;
for (int i = 0, j = k; j < p[u].c; j++, i++)p[u].s[i] = p[u].s[j];
p[u].c -= k;
}
}
void get(int k) //获取光标后k个字母
{
if (y + 1 + k <= p[x].c) {
for (int i = y + 1; i <= y + k; i++)putchar(p[x].s[i]);
}
else {
k -= (p[x].c - y - 1);
for (int i = y + 1; i < p[x].c; i++)putchar(p[x].s[i]);
int cur = x;
while (p[cur].r and k >= p[p[cur].r].c) {
k -= p[p[cur].r].c;
for (int i = 0; i < p[p[cur].r].c; i++)putchar(p[p[cur].r].s[i]);
cur = p[cur].r;
}
int u = p[cur].r;
for (int i = 0; i < k; i++)putchar(p[u].s[i]);
}
puts("");
}
void prev() //光标前移
{
if (y) y--;
else {
x = p[x].l;
y = p[x].c - 1;
}
}
void next() //光标后移
{
if (y != p[x].c - 1) {
y++;
}
else {
x = p[x].r;
y = 0;
}
}
void merge() //关键操作,将长度较短的合并，保持正确的复杂度
{
for (int i = p[0].r; i; i = p[i].r) {
while (p[i].r and p[i].c + p[p[i].r].c < N) {
int r = p[i].r;
for (int ii = p[i].c, j = 0; j < p[r].c; ii++, j++) {
p[i].s[ii] = p[r].s[j];
}
if (x == r) x = i, y += p[i].c;
p[i].c += p[r].c;
del(r);
}
}
}
int main() {
for (int i = 1; i < M; i++) id[++idx] = i;
scanf("%d", &n);
char op[10];
str[0] = '>';
insert(1); // 插入哨兵
move(1); // 将光标移动到哨兵后面
while (n--)
{
int a;
scanf("%s", op);
if (!strcmp(op, "Move"))
{
scanf("%d", &a);
move(a + 1);
}
else if (!strcmp(op, "Insert"))
{
scanf("%d", &a);
int i = 0, k = a;
while (a)
{
str[i] = getchar();
if (str[i] >= 32 && str[i] <= 126) i++, a--;
}
insert(k);
merge();
}
else if (!strcmp(op, "Delete"))
{
scanf("%d", &a);
remove(a);
merge();
}
else if (!strcmp(op, "Get"))
{
scanf("%d", &a);
get(a);
}
else if (!strcmp(op, "Prev")) prev();
else next();
}
}
rope 版本
/*
* @Author: zhl
* @Date: 2020-11-18 10:28:37
*/
#include <bits/stdc++.h>
#include <ext/rope>
using namespace std;
using namespace __gnu_cxx;
char str[2000010];
int main(){
rope<char> rp;int pos = 0;
int n;
scanf("%d", &n);
char op[10];
while (n--)
{
int a;
scanf("%s", op);
if (!strcmp(op, "Move"))
{
scanf("%d", &pos);
}
else if (!strcmp(op, "Insert"))
{
scanf("%d", &a);
str[a] = '\0';// Important！！！
int i = 0, k = a;
while (a)
{
str[i] = getchar();
if (str[i] >= 32 && str[i] <= 126) i++, a--;
}
rp.insert(pos,str);
}
else if (!strcmp(op, "Delete"))
{
scanf("%d", &a);
rp.erase(pos,a);
}
else if (!strcmp(op, "Get"))
{
scanf("%d", &a);a--;
for(int i = pos;i <= pos + a;i++)putchar(rp[i]);
puts("");
}
else if (!strcmp(op, "Prev")) pos--;
else pos++;
}
}
6.8 莫队
分块思想
分块思想其实是一种暴力
还是 【线段树1】洛谷模板
我们可以把它分成 \(\sqrt n, \sqrt n,..., \sqrt n\) 这样的一个一个块。
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5 + 10, M = 350;
int id[N], w[N];
ll sum[M], lz[M];
int n, m, len;
void updt(int l, int r, int v) {
if (id[l] == id[r]) {
for (int i = l; i <= r; i++) w[i] += v, sum[id[i]] += v;
return;
}
int i = l, j = r;
while (id[i] == id[l])w[i] += v, sum[id[i]] += v, i++;
while (id[j] == id[r])w[j] += v, sum[id[j]] += v, j--;
for (int k = id[i]; k <= id[j]; k++)sum[k] += 1ll * len * v, lz[k] += v;
}
ll query(int l, int r) {
ll res = 0;
if (id[l] == id[r]) {
for (int i = l; i <= r; i++) res += w[i] + lz[id[i]];
return res;
}
int i = l, j = r;
while (id[i] == id[l]) res += w[i] + lz[id[i]], i++;
while (id[j] == id[r]) res += w[j] + lz[id[j]], j--;
for (int k = id[i]; k <= id[j]; k++) res += sum[k];
return res;
}
int main() {
scanf("%d%d", &n, &m);
len = sqrt(n);
for (int i = 1; i <= n; i++) scanf("%d", w + i), id[i] = i / len, sum[id[i]] += w[i];
while (m--) {
int op, a, b, c;
scanf("%d", &op);
if (op == 1) {
scanf("%d%d%d", &a, &b, &c);
updt(a, b, c);
}
else {
scanf("%d%d", &a, &b);
printf("%lld\n", query(a, b));
}
}
}
普通莫队
求区间不同数的个数
/*
* @Author: zhl
* @LastEditTime: 2020-12-09 10:31:44
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int n, q, A[N], cnt[N], ID[N];
struct query {
int l, r, id;
bool operator < (const query& b)const {
return ID[l] == ID[b.l] ? r < b.r : ID[l] < ID[b.l];
}
}Q[N];
int res, ans[N];
void del(int idx) {
if (!--cnt[A[idx]])res--;
}
void add(int idx) {
if (!cnt[A[idx]]++)res++;
}
int main() {
scanf("%d", &n); int t = sqrt(n);
for (int i = 1; i <= n; i++)scanf("%d", A + i), ID[i] = i / t;
scanf("%d", &q);
for (int i = 1; i <= q; i++)scanf("%d%d", &Q[i].l, &Q[i].r), Q[i].id = i;
sort(Q + 1, Q + 1 + q);
int l = 1, r = 0;
for (int i = 1; i <= q; i++) {
int ql = Q[i].l, qr = Q[i].r;
while (l < ql)del(l++);
while (l > ql)add(--l);
while (r < qr)add(++r);
while (r > qr)del(r--);
ans[Q[i].id] = res;
}
for (int i = 1; i <= q; i++)printf("%d\n", ans[i]);
}
带修改的莫队
墨墨购买了一套N支彩色画笔（其中有些颜色可能相同），摆成一排，你需要回答墨墨的提问。墨墨会向你发布如下指令：
1、 Q L R代表询问你从第L支画笔到第R支画笔中共有几种不同颜色的画笔。
2、 R P Col 把第P支画笔替换为颜色Col。
为了满足墨墨的要求，你知道你需要干什么了吗？
就是在基础的莫队上增加了修改操作
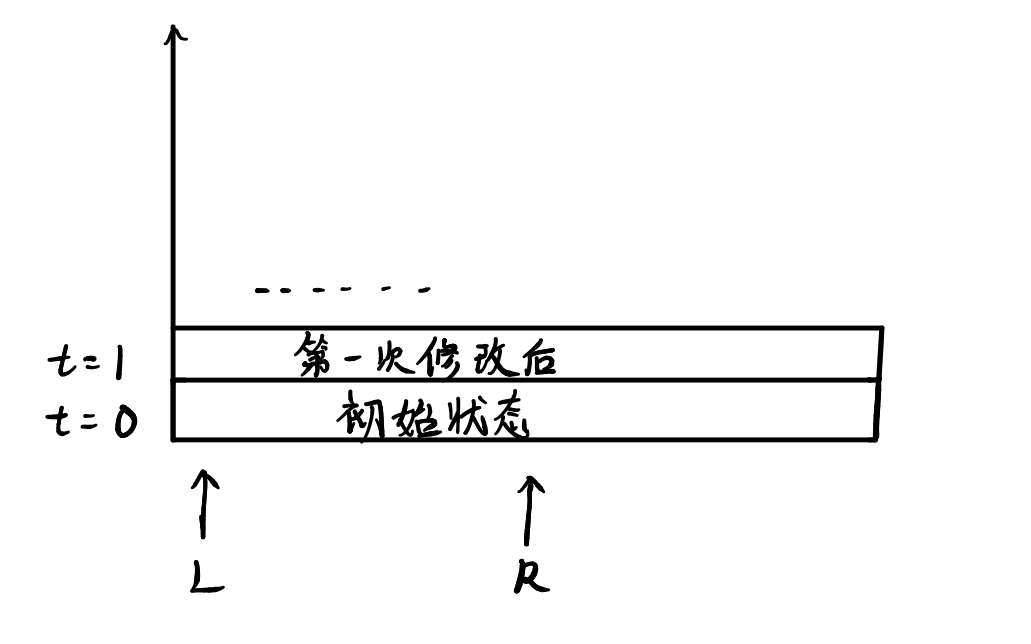
所以需要挪动三个指针 \(L\) , \(R\) , \(t\)
有个小技巧
while (t < qt) {
t++;
if (ql <= m[t].pos and m[t].pos <= qr) {
del(A[m[t].pos]);
add(m[t].val);
}
swap(A[m[t].pos], m[t].val);
}
while (t > qt) {
if (ql <= m[t].pos and m[t].pos <= qr) {
del(A[m[t].pos]);
add(m[t].val);
}
swap(A[m[t].pos], m[t].val);
t--;
}
这个 \(swap\) 操作就很灵性
块大小为 \(^3\sqrt {nt}\) 的时候达到理论最快复杂度， 然而我 \(TLE\) 了 wrnm
我这份代码 len = cbrt(1.0 * n * mcnt) + 1; 会被卡一个点
前两个块大小 \(n ^ {\frac 2 3}\) 和 \(n^{\frac 3 4}\) 都可以通过, 0.75跑的最快。
改成第三份理论最优就 TLE ？ 难道又是我的毒瘤代码的锅
//len = pow(n ,0.6667);
len = pow(n, 0.75);
//len = pow(n * mcnt, 0.333) + 1;
/*
* @Author: zhl
* @Date: 2020-11-19 10:39:02
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 150000;
int A[N], cnt[1000010], block[N];
int n, mm, len;
struct query {
int id, l, r, t;
bool operator < (const query& rhs)const {
int al = block[l], bl = block[rhs.l];
int ar = block[r], br = block[rhs.r];
if (al != bl)return al < bl;
if (ar != br)return ar < br;
return t < rhs.t;
}
}q[N];
struct modify {
int pos, val;
}m[N];
long long qcnt, mcnt, ans[N], now;
void del(int x) {
if (!--cnt[x])now--;
}
void add(int x) {
if (!cnt[x]++)now++;
}
signed main() {
scanf("%d%d", &n, &mm);
for (int i = 1; i <= n; i++)scanf("%d", A + i);
while (mm--) {
char op[2]; int a, b;
scanf("%s%d%d", op, &a, &b);
if (*op == 'Q') {
qcnt++;
q[qcnt] = { qcnt,a,b, mcnt };
//q[qcnt] = { ++qcnt,a,b,mcnt };
}
else {
m[++mcnt] = { a,b };
}
}
len = pow(n ,0.6667);
for (int i = 1; i <= n; i++)block[i] = i / len;
sort(q + 1, q + 1 + qcnt);
int l = 1, r = 0, t = 0;
for (int i = 1; i <= qcnt; i++) {
int ql = q[i].l, qr = q[i].r, qt = q[i].t;
while (l < ql) del(A[l++]);
while (l > ql) add(A[--l]);
while (r < qr) add(A[++r]);
while (r > qr) del(A[r--]);
while (t < qt) {
t++;
if (ql <= m[t].pos and m[t].pos <= qr) {
del(A[m[t].pos]);
add(m[t].val);
}
swap(A[m[t].pos], m[t].val);
}
while (t > qt) {
if (ql <= m[t].pos and m[t].pos <= qr) {
del(A[m[t].pos]);
add(m[t].val);
}
swap(A[m[t].pos], m[t].val);
t--;
}
ans[q[i].id] = now;
}
for (int i = 1; i <= qcnt; i++)printf("%d\n", ans[i]);
}
回滚莫队
题意：
查询区间 \([l,r]\) 内一个数乘上它在区间出现次数的最大值
使用莫队的时候进行增加操作的时候会很简单，但是在删除操作的时候不是那么好维护的时候，可以使用不删除的莫队（回滚莫队)
还是相同的思路，先把询问排序
然后对于左端点在同一个块的询问来说
如图
如果右端点也在块内，则暴力计算
否则左端点从下一个块的左边开始，右端点单调向右移动。
左端点在块内反复进行回滚操作。
这样就在保证时间复杂度还是 \(O(n\sqrt n)\) 的情况下避免了删除操作
/*
* @Author: zhl
* @Date: 2020-11-19 10:38:35
*/
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5 + 10;
int n, m, len, cnt[N], nums[N], w[N], ID[N];
ll ans[N];
struct Query {
int id, l, r;
bool operator < (const Query& rhs)const {
int al = ID[l], bl = ID[rhs.l];
if (al != bl)return al < bl;
return r < rhs.r;
}
}q[N];
void add(int x, ll& res) {
cnt[x]++;
res = max(res, 1ll * cnt[x] * nums[x]);
}
int main() {
scanf("%d%d", &n, &m);
int numID = 0;
for (int i = 1; i <= n; i++)scanf("%d", w + i), nums[++numID] = w[i];
sort(nums + 1, nums + 1 + n);
numID = unique(nums + 1, nums + 1 + n) - nums - 1;
len = sqrt(n);
for (int i = 1; i <= n; i++)ID[i] = i / len;
for (int i = 1; i <= n; i++)w[i] = lower_bound(nums + 1, nums + 1 + numID, w[i]) - nums;
for (int i = 1; i <= m; i++) {
scanf("%d%d", &q[i].l, &q[i].r);
q[i].id = i;
}
sort(q + 1, q + 1 + m);
for (int x = 1; x <= m;) {
int y = x;
while (y <= m and ID[q[y].l] == ID[q[x].l]) y++;
//块内暴力
int right = len * ID[q[x].l] + len;
//int right = len * ID[q[y].l]; 这样不对,y不一定比x大
while (x < y and q[x].r <= right - 1) {
ll res = 0;
for (int i = q[x].l; i <= q[x].r; i++) add(w[i], res);
ans[q[x].id] = res;
for (int i = q[x].l; i <= q[x].r; i++) cnt[w[i]]--;
x++;
}
//块外
int l = right, r = right - 1;
ll res = 0;
while (x < y) {
int ql = q[x].l, qr = q[x].r;
while (r < qr)add(w[++r], res);
ll _res = res;
while (l > ql)add(w[--l], res);
ans[q[x].id] = res;
while (l < right) cnt[w[l++]] --;
res = _res;
x++;
}
memset(cnt, 0, sizeof cnt);
}
for (int i = 1; i <= m; i++)printf("%lld\n", ans[i]);
}
给定一个序列，多次询问一段区间 \([l,r]\)，求区间中相同的数的最远间隔距离。
序列中两个元素的间隔距离指的是两个元素下标差的绝对值。
这个说是模板题，其实上一道题更模板。
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int w[N], ans[N], n, m, nums[N], ID[N], len;
int fir[N], last[N];
int mfir[N], mlast[N], mpos[N], mcnt, vis[N], vscnt;
struct Query {
int id, l, r;
bool operator < (const Query& b)const {
if (ID[l] != ID[b.l])return ID[l] < ID[b.l];
return r < b.r;
}
}q[N];
void add(int pos, int val, int& res) {
if (!fir[val]) fir[val] = pos;
else fir[val] = min(fir[val], pos);
if (!last[val])last[val] = pos;
else last[val] = max(last[val], pos);
res = max(res, last[val] - fir[val]);
}
int main() {
scanf("%d", &n);
int numID = 0;
for (int i = 1; i <= n; i++)scanf("%d", w + i), nums[++numID] = w[i];
sort(nums + 1, nums + 1 + n);
numID = unique(nums + 1, nums + 1 + n) - nums - 1;
for (int i = 1; i <= n; i++)w[i] = lower_bound(nums + 1, nums + 1 + numID, w[i]) - nums;
len = sqrt(n);
for (int i = 1; i <= n; i++)ID[i] = i / len;
scanf("%d", &m);
for (int i = 1; i <= m; i++) {
scanf("%d%d", &q[i].l, &q[i].r); q[i].id = i;
}
sort(q + 1, q + 1 + m);
for (int x = 1; x <= m;) {
int y = x;
while (y <= m and ID[q[y].l] == ID[q[x].l])y++;
int right = ID[q[x].l] * len + len;
while (x < y and q[x].r <= right - 1) {
int res = 0, mcnt = 0; vscnt++;
for (int i = q[x].l; i <= q[x].r; i++) {
if (vis[w[i]] != vscnt) {
vis[w[i]] = vscnt;
mpos[++mcnt] = w[i];
mfir[mcnt] = fir[w[i]];
mlast[mcnt] = last[w[i]];
}
add(i, w[i], res);
}
ans[q[x].id] = res;
for (int i = 1; i <= mcnt; i++) {
fir[mpos[i]] = mfir[i];
last[mpos[i]] = mlast[i];
}
x++;
}
int l = right, r = right - 1;
int res = 0;
while (x < y) {
int ql = q[x].l, qr = q[x].r;
while (r < qr)r++, add(r, w[r], res);
int _res = res;
mcnt = 0; vscnt++;
while (l > ql) {
l--;
if (vis[w[l]] != vscnt) {
vis[w[l]] = vscnt;
mpos[++mcnt] = w[l];
mfir[mcnt] = fir[w[l]];
mlast[mcnt] = last[w[l]];
}
add(l, w[l], res);
}
ans[q[x].id] = res;
for (int i = 1; i <= mcnt; i++) {
fir[mpos[i]] = mfir[i];
last[mpos[i]] = mlast[i];
}
l = right; res = _res;
x++;
}
memset(fir, 0, sizeof fir); memset(last, 0, sizeof last);
}
for (int i = 1; i <= m; i++)printf("%d\n", ans[i]);
}
树上莫队
SP10707 COT2 - Count on a tree II - 洛谷
- 给定 \(n\) 个结点的树，每个结点有一种颜色。
- \(m\) 次询问，每次询问给出 \(u,v\)，回答 \(u,v\) 之间的路径上的结点的不同颜色数。
很显然，如果是在序列上的化就是最基础的莫队模板题
考虑转化到序列上
欧拉序列 即 \(DFS\) 序
可以解决这个问题
对于询问 \((x,y)\) 让 \(x\) 是在 \(DFS\) 中先出现的那个
分为两种情况：
- \(x == lca(x,y)\) , 则对应的区间是 \([in(x),in(y)]\) 中出现次数为一的点 ,如上图红色询问
- \(x \neq lca(x,y)\) , 则对应区间是 \([out(x), in(y)]\) 中出现次数为一的点，加上 \(lca\)
对于翻转操作，可以用一个数组 \(st\) 进行标识，增添和删除其实都是一样的
/*
* @Author: zhl
* @Date: 2020-11-19 15:34:09
*/
#include<bits/stdc++.h>
#pragma GCC optimize(3)
#define pb(x) push_back(x)
using namespace std;
const int N = 1e5 + 10;
vector<int>G[N];
int n, m, len, ID[N], ans[N];
int w[N], nums[N], in[N], out[N], ord[N];
int tot, dep[N], f[N][32], cnt[N], st[N];
void add(int x, int& res) {
st[x] ^= 1;
if (!st[x]) {
if (!--cnt[w[x]])res--;
}
else {
if (!cnt[w[x]]++)res++;
}
}
void dfs(int u, int p) {
in[u] = ++tot;
ord[tot] = u;
dep[u] = dep[p] + 1; f[u][0] = p;
for (int x = 1; (1 << x) < dep[u]; x++) {
f[u][x] = f[f[u][x - 1]][x - 1];
}
for (int v : G[u]) {
if (v == p)continue;
dfs(v, u);
}
out[u] = ++tot;
ord[tot] = u;
}
int LCA(int x, int y) {
if (dep[x] < dep[y])swap(x, y);
while (dep[x] != dep[y]) {
int u = dep[x] - dep[y];
int v = 0;
while (!(u & (1 << v)))v++;
x = f[x][v];
}
while (x != y) {
int v = 0;
while (f[x][v] != f[y][v])v++;
x = f[x][max(0, v - 1)]; y = f[y][max(0, v - 1)];
}
return x;
}
struct Query {
int id, l, r, lca;
bool operator < (const Query& b)const {
if (ID[l] != ID[b.l])return ID[l] < ID[b.l];
return r < b.r;
}
}q[N];
int main() {
scanf("%d%d", &n, &m); int numID = 0;
for (int i = 1; i <= n; i++)scanf("%d", w + i), nums[++numID] = w[i];
sort(nums + 1, nums + 1 + n);
numID = unique(nums + 1, nums + 1 + n) - nums - 1;
for (int i = 1; i <= n; i++)w[i] = lower_bound(nums + 1, nums + 1 + numID, w[i]) - nums;
for (int i = 1; i < n; i++) {
int a, b; scanf("%d%d", &a, &b);
G[a].pb(b); G[b].pb(a);
}
dfs(1, 0);
len = sqrt(tot);
for (int i = 1; i <= tot; i++)ID[i] = i / len;
for (int i = 1; i <= m; i++) {
int x, y; scanf("%d%d", &x, &y);
int lca = LCA(x, y);
if (in[x] > in[y])swap(x, y);
if (lca == x) {
q[i] = { i,in[x],in[y],0 };
}
else {
q[i] = { i,out[x],in[y],lca };
}
}
sort(q + 1, q + 1 + m);
int res = 0, l = 1, r = 0;
for (int i = 1; i <= m; i++) {
int ql = q[i].l, qr = q[i].r, lca = q[i].lca;
if (lca != 0)add(lca, res);
while (l < ql)add(ord[l++], res);
while (l > ql)add(ord[--l], res);
while (r < qr)add(ord[++r], res);
while (r > qr)add(ord[r--], res);
ans[q[i].id] = res;
if (lca != 0)add(lca, res);
}
for (int i = 1; i <= m; i++)printf("%d\n", ans[i]);
}
二次离线莫队
P4887 【模板】莫队二次离线（第十四分块(前体)） - 洛谷
给一个序列 \(a\) ，每次给一个查询区间 \([l,r]\)
查询 \(l \le i < j \le r\) 且 \(a_i\) 异或 \(a_j\) 正好有 \(k\) 个二进制 \(bit\) 的个数
还是用莫队的思想，在挪的时候更新答案的方式如图
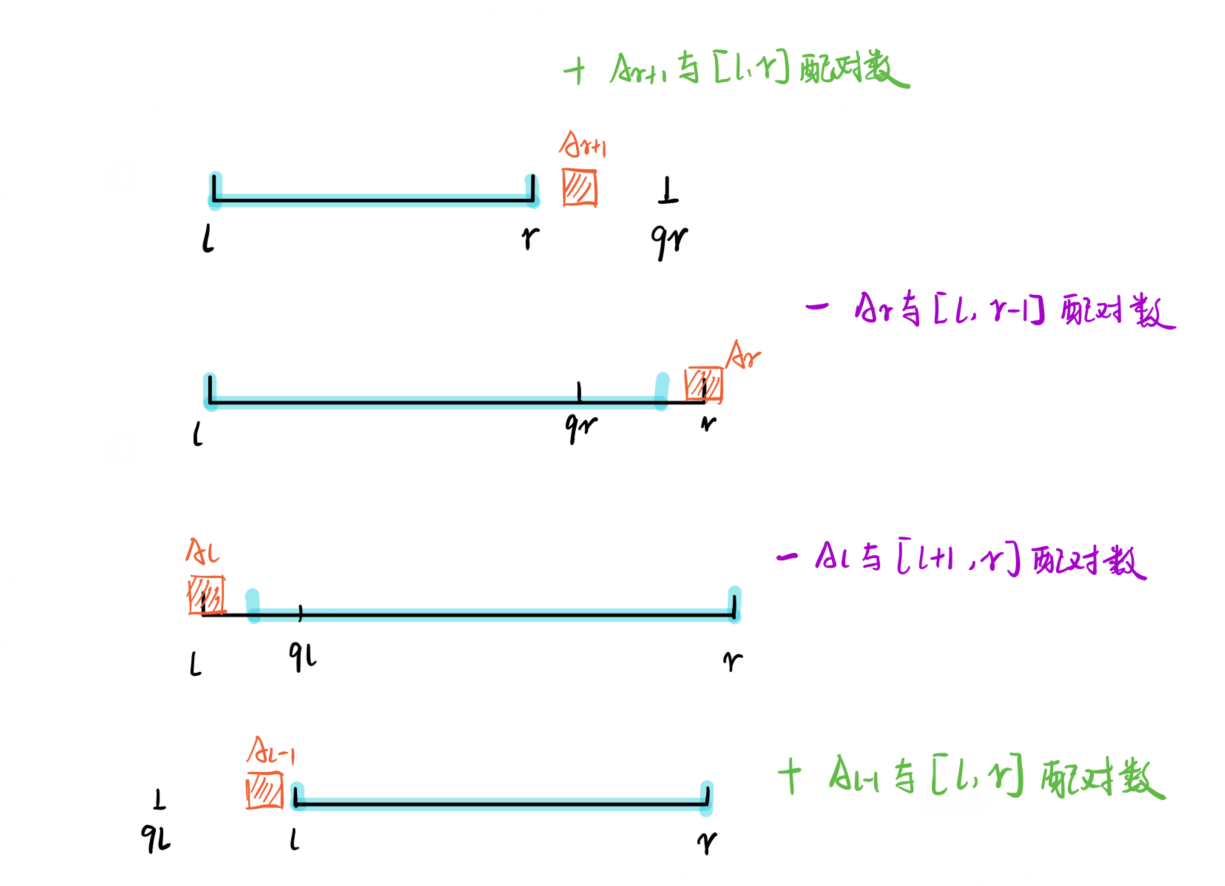
现在我们要解决的问题是如何求 \(A_i\) 与区间 \([L,R]\) 的配对数。
这里我们利用前缀和的思想，令 \(S_R\) 表示区间 \([1,R]\) 与 \(A_i\) 的配对数
则要求的就是 \(S_R - S_{L-1}\)
两个数配对指的是异或满足题目
我们可以设 \(f[i]\) 表示 \([1,i]\) 与 \(A_{i+1}\) 的配配对数目所以对于上图的情况有一个\(S\) 可以用 \(f\) 来表示，还有一个就再次离线，挂到对应的点上。
求出 \(f\) 数组
vector<int>nums;
for (int i = 0; i < (1 << 14); i++)
if (count(i) == k)nums.push_back(i);
for (int i = 1; i <= n; i++) {
for (int v : nums)g[w[i] ^ v]++;
f[i] = g[w[i + 1]];
}
举例当 \(r < qr\) 时
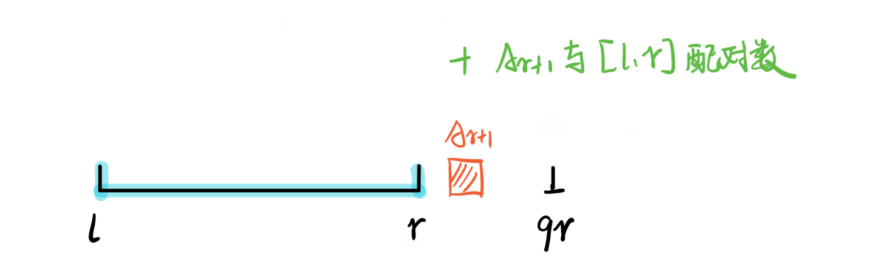
if (r < qr)subs[l - 1].push_back({ i, r + 1, qr, -1 });
while (r < qr) q[i].res += f[r++];
每一次挪动都要加上 \(f[r]\) 还要减去区间 \([1,l-1]\) 与 \(A_{r+1},A_{r+2},...,A_{qr}\) 的配对数目，对于这个东西，可以把它挂到 \(l-1\) 上， 这个挂挺形象的。
后面挪 \(l\) 的时候要注意自己跟自己匹配的情况，只有 \(k == 0\) 的时候自己可以匹配自己。
注意自己是不能匹配自己的，但是这种情况在计算 \(S\) 的时候是被计算在内的。
最后处理离线查询
memset(g, 0, sizeof g);
for (int i = 1; i <= n; i++) {
for (int v : nums)g[v ^ w[i]]++;
for (auto& x : subs[i]) {
for (int i = x.l; i <= x.r; i++) {
q[x.id].res += x.t * g[w[i]];
}
}
}
这一块的复杂度是 \(r\) 的移动次数 \(O(n \sqrt n)\) 量级
/*
* @Author: zhl
* @Date: 2020-11-19 20:16:41
*/
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
int n, m, k, len, ID[N], f[N], g[N], w[N];
ll ans[N];
struct Query {
int id, l, r;
ll res;
bool operator < (const Query& b)const {
if (ID[l] != ID[b.l]) return ID[l] < ID[b.l];
return r < b.r;
}
}q[N];
struct subquery {
int id, l, r, t;
};
vector<subquery>subs[N];
int count(int n) {
int ans = 0;
while (n) ans++, n -= -n & n;
return ans;
}
int main() {
scanf("%d%d%d", &n, &m, &k);
for (int i = 1; i <= n; i++)scanf("%d", w + i);
len = sqrt(n);
for (int i = 1; i <= n; i++)ID[i] = i / len;
vector<int>nums;
for (int i = 0; i < (1 << 14); i++)if (count(i) == k)nums.push_back(i);
for (int i = 1; i <= n; i++) {
for (int v : nums)g[w[i] ^ v]++;
f[i] = g[w[i + 1]];
}
for (int i = 1; i <= m; i++) {
scanf("%d%d", &q[i].l, &q[i].r); q[i].id = i;
}
sort(q + 1, q + 1 + m);
int l = 1, r = 0;
for (int i = 1; i <= m; i++) {
int ql = q[i].l, qr = q[i].r;
//在 l - 1 处 挂上一个离线查询
if (r < qr)subs[l - 1].push_back({ i, r + 1, qr, -1 });
while (r < qr) q[i].res += f[r++];
if (r > qr)subs[l - 1].push_back({ i, qr + 1,r ,1 });
while (r > qr) q[i].res -= f[--r];
if (l < ql)subs[r].push_back({ i, l, ql - 1, -1 });
while (l < ql) q[i].res += f[l - 1] + !k, l++;
if (l > ql)subs[r].push_back({ i, ql, l - 1,1 });
while (l > ql) q[i].res -= f[l - 2] + !k, l--;
}
memset(g, 0, sizeof g);
for (int i = 1; i <= n; i++) {
for (int v : nums)g[v ^ w[i]]++;
for (auto& x : subs[i]) {
for (int i = x.l; i <= x.r; i++) {
q[x.id].res += x.t * g[w[i]];
}
}
}
for (int i = 2; i <= m; i++) q[i].res += q[i - 1].res;
for (int i = 1; i <= m; i++)ans[q[i].id] = q[i].res;
for (int i = 1; i <= m; i++)printf("%lld\n", ans[i]);
}
6.9 树套树
一种思想，就是一棵树的节点是另一颗树。
在外面的叫外层树，在里面的叫内层树。
外层树一般是， 树状数组， 线段树
内层树一般是 平衡树 ， STL , 线段树
线段树套STL
/*
* @Author: zhl
* @Date: 2020-11-16 12:50:32
*/
#include<bits/stdc++.h>
#define lo (o<<1)
#define ro (o<<1|1)
#define mid (l+r>>1)
using namespace std;
const int N = 5e4 + 10, inf = 1e9;
multiset<int>s[N << 2];
int A[N];
void build(int o, int l, int r) {
s[o].insert(inf); s[o].insert(-inf);
for (int i = l; i <= r; i++) s[o].insert(A[i]);
if (l == r)return;
build(lo, l, mid);
build(ro, mid + 1, r);
}
void updt(int o, int l, int r, int pos, int v) {
s[o].erase(s[o].lower_bound(A[pos]));
s[o].insert(v);
if (l == r)return;
if (pos <= mid) updt(lo, l, mid, pos, v);
else updt(ro, mid + 1, r, pos, v);
}
int query(int o, int l, int r, int L, int R, int v) {
if (L <= l and r <= R) return *prev(s[o].lower_bound(v));
int ans = -inf;
if (L <= mid)ans = max(ans, query(lo, l, mid, L, R, v));
if (R > mid) ans = max(ans, query(ro, mid + 1, r, L, R, v));
return ans;
}
int n, m;
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)scanf("%d", A + i);
build(1, 1, n);
while (m--) {
int op, a, b, x; scanf("%d", &op);
if (op == 1) {
scanf("%d%d", &a, &b);
updt(1, 1, n, a, b);
A[a] = b;
}
else {
scanf("%d%d%d", &a, &b, &x);
printf("%d\n", query(1, 1, n, a, b, x));
}
}
}
线段树套平衡树
很多棵树的时候可以开一个 root 数组就可以，这样可以不需要传引用，因为在splay的时候会更新 root数组
rotate 不可以任意顺序，会有影响
/*
* @Author: zhl
* @Date: 2020-11-16 13:51:18
*/
#include<bits/stdc++.h>
#define mid (l+r>>1)
#define lo (o<<1)
#define ro (o<<1|1)
using namespace std;
const int N = 2e6 + 10, inf = 0x7fffffff;
struct node {
int s[2], size, p, v;
void init(int _p, int _v) {
p = _p; v = _v; size = 1;
}
}tr[N];
int w[N], n, m, root[N], idx;
void push_up(int u) {
tr[u].size = tr[tr[u].s[0]].size + tr[tr[u].s[1]].size + 1;
}
void rotate(int x) {
int y = tr[x].p, z = tr[y].p;
int k = tr[y].s[1] == x;
tr[z].s[tr[z].s[1] == y] = x; tr[x].p = z;
tr[y].s[k] = tr[x].s[k ^ 1]; tr[tr[x].s[k ^ 1]].p = y; //草这两行顺序不能换
tr[x].s[k ^ 1] = y; tr[y].p = x;
push_up(y), push_up(x);
}
void splay(int x, int k,int rt) {
while (tr[x].p != k) {
int y = tr[x].p, z = tr[y].p;
if (z != k) {
if ((tr[z].s[0] == y) ^ (tr[y].s[0] == x)) rotate(x);
else rotate(y);
}
rotate(x);
}
if (!k)root[rt] = x;
}
void insert(int v, int rt) {
int u = root[rt], p = 0;
while (u) p = u, u = tr[u].s[v > tr[u].v];
u = ++idx;
if (p)tr[p].s[v > tr[p].v] = u;
tr[u].init(p, v);
splay(u, 0, rt);
}
int get_rank(int v, int rt) {
int u = root[rt], res = 0;
while (u) {
if (v > tr[u].v) res += tr[tr[u].s[0]].size + 1, u = tr[u].s[1];
else u = tr[u].s[0];
}
return res;
}
void build(int o, int l, int r) {
insert(-inf, o); insert(inf, o);
for (int i = l; i <= r; i++) {
insert(w[i], o);
}
if (l == r)return;
build(lo, l, mid);
build(ro, mid + 1, r);
}
int query_rank(int o, int l, int r, int L, int R, int x) {
if (L <= l and r <= R)return get_rank(x, o) - 1;
int ans = 0;
if (L <= mid)ans += query_rank(lo, l, mid, L, R, x);
if (R > mid) ans += query_rank(ro, mid + 1, r, L, R, x);
return ans;
}
void updt(int o, int l, int r, int pos, int v){
int u = root[o];
while (u) {
if (tr[u].v == w[pos])break;
if (w[pos] > tr[u].v)u = tr[u].s[1];
if (w[pos] < tr[u].v) u = tr[u].s[0];
}
splay(u, 0, o);
int ls = tr[u].s[0], rs = tr[u].s[1];
while (tr[ls].s[1]) ls = tr[ls].s[1];
while (tr[rs].s[0]) rs = tr[rs].s[0];
splay(ls, 0, o); splay(rs, ls, o);
tr[rs].s[0] = 0;
push_up(rs); push_up(ls);
insert(v, o);
if (l == r)return; //不要忘记结束条件
if (pos <= mid) {
updt(lo, l, mid, pos, v);
}
else {
updt(ro, mid + 1, r, pos, v);
}
}
int get_pre(int x,int rt) {
int u = root[rt], res = -inf;
while (u) {
if (tr[u].v >= x) u = tr[u].s[0];
else res = tr[u].v, u = tr[u].s[1];
}
return res;
}
int get_suc(int x,int rt) {
int u = root[rt], res = -inf;
while (u) {
if (tr[u].v <= x) u = tr[u].s[1];
else res = tr[u].v, u = tr[u].s[0];
}
return res;
}
int query_pre(int o, int l, int r, int L, int R, int x) {
if (L <= l and r <= R)return get_pre(x, o);
int ans = -inf;
if (L <= mid)ans = max(ans, query_pre(lo, l, mid, L, R, x));
if (R > mid) ans = max(ans, query_pre(ro, mid + 1, r, L, R, x));
return ans;
}
int query_suc(int o, int l, int r, int L, int R, int x) {
if (L <= l and r <= R)return get_suc(x, o);
int ans = inf;
if (L <= mid)ans = min(ans, query_suc(lo, l, mid, L, R, x));
if (R > mid) ans = min(ans, query_suc(ro, mid + 1, r, L, R, x));
return ans;
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)scanf("%d", w + i);
build(1, 1, n);
while (m--) {
int op, a, b, k, pos;
scanf("%d", &op);
if (op == 1) {
scanf("%d%d%d", &a, &b, &k);
printf("%d\n", query_rank(1, 1, n, a, b, k) + 1);
}
else if (op == 2) {
scanf("%d%d%d", &a, &b, &k);
int l = 0, r = 1e8;
while (l < r) {
int m = l + r + 1 >> 1;
if (query_rank(1, 1, n, a, b, m) + 1 <= k) {
l = m;
}
else {
r = m - 1;
}
}
printf("%d\n", r);
}
else if (op == 3) {
scanf("%d%d", &pos, &k);
updt(1, 1, n, pos, k);
w[pos] = k;
}
else if (op == 4) {
scanf("%d%d%d", &a, &b, &k);
printf("%d\n", query_pre(1, 1, n, a, b, k));
}
else if (op == 5) {
scanf("%d%d%d", &a, &b, &k);
printf("%d\n", query_suc(1, 1, n, a, b, k));
}
}
}
权值线段树套线段树
之前没有做过权值线段树套外层树，也是第一次写动态开点的完整线段树
在push_down 的时候要动态开点。其实跟普通线段树是一样的。
写之前一定要先想清楚。外层的线段树是将值离散化后建的，外层的线段树可以用 o<<1 ， o<<1|1 ， 这样进行转移。内层的线段树需要动态开点，所以需要数组 lc[N] , rc[N]
要计算开的空间大小。
/*
* @Author: zhl
* @Date: 2020-11-17 13:55:59
*/
#include<bits/stdc++.h>
#define mid (l + r >> 1)
#define lo (o << 1)
#define ro (o << 1 | 1)
using ll = long long;
using namespace std;
const int N = 5e4 + 10, P = N * 17 * 17, M = 4 * N;
int n, m;
int root[M], lc[P], rc[P], lz[P], tot;
ll sum[P];
void push_down(int u,int l,int r) {
if (!lc[u])lc[u] = ++tot;
lz[lc[u]] += lz[u];
if (!rc[u])rc[u] = ++tot;
lz[rc[u]] += lz[u];
sum[lc[u]] += (mid - l + 1) * lz[u];
sum[rc[u]] += (r - mid) * lz[u];
lz[u] = 0;
}
void updt(int& rt, int L,int R, int o = 1, int l = 1, int r = n) {
if (!rt) rt = ++tot;
if (L <= l and r <= R) {
lz[rt] ++;
//sum[rt] += R - L + 1;//我是傻逼草
sum[rt] += r - l + 1;
return;
}
if (lz[rt])push_down(rt, l , r);
if (L <= mid)updt(lc[rt], L, R, lo, l, mid);
if (R > mid)updt(rc[rt], L, R, ro, mid + 1, r);
sum[rt] = sum[lc[rt]] + sum[rc[rt]];
}
ll query(int rt, int L, int R, int o = 1, int l = 1, int r = n) {
if (!rt)return 0;
if (L <= l and r <= R) {
return sum[rt];
}
if (lz[rt])push_down(rt, l, r);
ll ans = 0;
if (L <= mid)ans += query(lc[rt], L, R, lo, l, mid);
if (R > mid) ans += query(rc[rt], L, R, ro, mid + 1, r);
return ans;
}
int cntID, id[N];
void add(int L,int R, int pos, int o = 1, int l = 1, int r = cntID) {
updt(root[o], L, R);
if (l == r)return;
if (pos <= mid)add(L, R, pos, lo, l, mid);
else add(L, R, pos, ro, mid + 1, r);
}
int get_kth(int L,int R,ll k,int o = 1, int l = 1, int r = cntID) {
if (l == r)return id[l];
ll num = query(root[ro], L, R);
if (num >= k) return get_kth(L, R, k, ro, mid + 1, r);
else return get_kth(L, R, k - num, lo, l, mid);
}
struct {
int op, a, b, c;
}q[N];
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
scanf("%d%d%d%d", &q[i].op, &q[i].a, &q[i].b, &q[i].c);
if (q[i].op == 1) {
id[++cntID] = q[i].c;
}
}
sort(id + 1, id + 1 + cntID);
cntID = unique(id + 1, id + 1 + cntID) - id - 1;
for (int i = 1; i <= m; i++) {
if (q[i].op == 1)q[i].c = lower_bound(id + 1, id + 1 + cntID, q[i].c) - id;
}
for (int i = 1; i <= m; i++) {
if (q[i].op == 1) {
add(q[i].a, q[i].b, q[i].c);
}
else {
printf("%d\n", get_kth(q[i].a, q[i].b, q[i].c));
}
}
}
6.10 LCT
\(LCT\) 可以动态维护一个森林
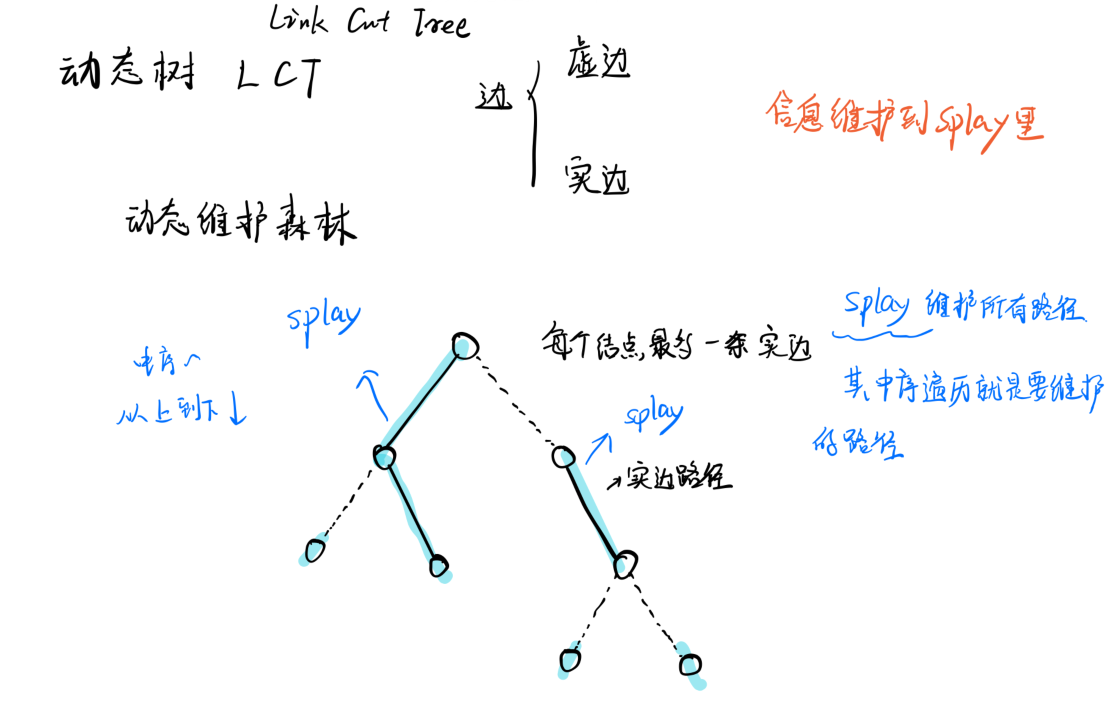
每个节点最多只能连接一条实边 ，被父亲节点指向的实边不属于自己的实边。
实边和虚边是维护的一种方式，实边和虚边在原图中都是真实存在的边。
一棵树中的实边和虚边可以相互变换
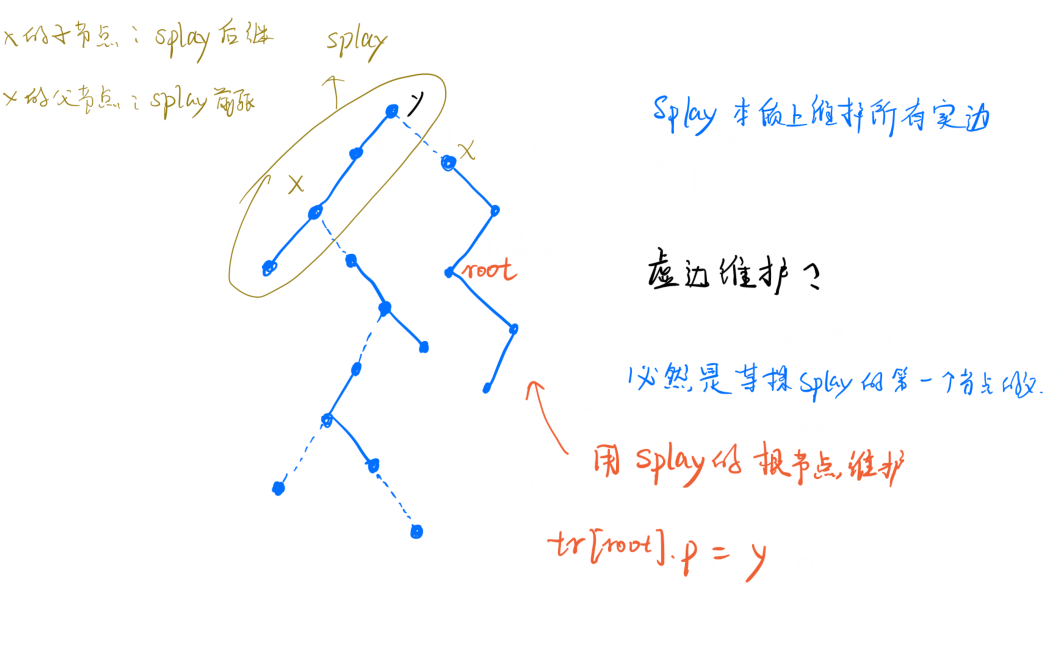
用 \(Splay\) 维护所有的实边
基本操作
Access(x)
将 \(x\) 所在的树的根节点与 \(x\) 之间的路径变成实边路径
并且将 \(x\) 旋转至该实边路径 \(Splay\) 的根节点
不改变原树的结构
make_root(x)
将 \(x\) 变成根节点，这个根节点指的是原树的根节点
find_root(x)
找到 \(x\) 所在树的根节点
将根节点与 \(x\) 之间的路径变成实边路径，并且将 原树的根节点 旋转到 \(Splay\) 的根节点
split(x,y)
将 \(x\) 和 \(y\) 建立一条实边路径
先连通根节点和 \(x\) 成为实体路径，然后将 \(x\) 变成根
然后连通根节点 \(x\) 和 \(y\)
link(x,y)
若 \(x\) , \(y\) 不连通，则建立一条虚边
cut(x,y)
若 \(x\) , \(y\) 存在边，则删除它
/*
* @Author: zhl
* @Date: 2020-11-20 15:08:50
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, m;
struct node {
int s[2], p, v;
int sum, rev;
}tr[N];
int stk[N];
void rev(int x) {
swap(tr[x].s[0], tr[x].s[1]);
tr[x].rev ^= 1;
}
void push_up(int x) {
tr[x].sum = tr[tr[x].s[0]].sum ^ tr[tr[x].s[1]].sum ^ tr[x].v;
}
void push_down(int x) {
if (tr[x].rev) {
rev(tr[x].s[0]); rev(tr[x].s[1]);
tr[x].rev = 0;
}
}
bool is_root(int x) {
return tr[tr[x].p].s[0] != x and tr[tr[x].p].s[1] != x;
}
void rotate(int x) {
int y = tr[x].p, z = tr[y].p;
int k = tr[y].s[1] == x;
if (!is_root(y)) tr[z].s[tr[z].s[1] == y] = x;
tr[x].p = z;
tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
tr[x].s[k ^ 1] = y; tr[y].p = x;
push_up(y), push_up(x);
}
void splay(int x) {
int top = 0, r = x;
stk[++top] = r;
while (!is_root(r)) stk[++top] = r = tr[r].p;
while (top)push_down(stk[top--]);
while (!is_root(x)) {
int y = tr[x].p, z = tr[y].p;
if (!is_root(y)){
if((tr[y].s[0] == x) ^ (tr[z].s[0] == y))rotate(x);
else rotate(y);
}
rotate(x);
}
}
void access(int x) {
/*
将 x 所在的树的根节点与 x 之间的路径变成实边路径
并且将 x 旋转至该实边路径splay的根节点
*/
int z = x;
for (int y = 0; x; y = x, x = tr[x].p) {
splay(x);
tr[x].s[1] = y, push_up(x);
}
splay(z);
}
void make_root(int x) {
/*
将 x 变成 x 所在树中的根节点
*/
access(x);
rev(x);
}
int find_root(int x) {
/*
查询 x 所在树的根节点
将根节点与 x 之间的路径变成实边路径，并且将 原树的根节点 旋转到splay的根节点
*/
access(x);
while (tr[x].s[0])push_down(x), x = tr[x].s[0];
splay(x);
return x;
}
void split(int x, int y) {
/*
将 x 和 y 建立一条实边路径
先连通根节点和 x 成为实体路径，然后将 x 变成根
然后连通根节点 x 和 y
*/
make_root(x);
access(y);
}
void link(int x, int y) {
/*
若 x 和 y 不连通
建立一虚边
*/
make_root(x);
if (find_root(y) != x) tr[x].p = y;
}
void cut(int x, int y) {
/*
若 x， y 存在边
则删除它
*/
make_root(x);
if (find_root(y) == x and tr[y].p == x and !tr[y].s[0]) {
tr[x].s[1] = tr[y].p = 0;
push_up(x);
}
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)scanf("%d", &tr[i].v);
while (m--) {
int t, x, y;
scanf("%d%d%d", &t, &x, &y);
if (t == 0) {
split(x, y);
printf("%d\n", tr[y].sum);
}
else if (t == 1) link(x, y);
else if (t == 2) cut(x, y);
else {
splay(x);
tr[x].v = y;
push_up(x);
}
}
}
魔法森林
求路径上两种属性最大值之和的最小值
/*
* @Author: zhl
* @Date: 2020-11-20 15:08:42
*/
#include<bits/stdc++.h>
#pragma GCC optimize(2)
using namespace std;
const int N = 150010, INF = 1e9;
struct Edge {
int x, y, a, b;
bool operator < (const Edge& rhs)const {
return a < rhs.a;
}
}E[N];
struct node {
int s[2], p, v;
int mx; //最大值的下标
int rev;
}tr[N];
int n, m, fa[N];
int find(int a) { return a == fa[a] ? a : fa[a] = find(fa[a]); }
int stk[N];
void rev(int x) {
swap(tr[x].s[0], tr[x].s[1]);
tr[x].rev ^= 1;
}
void push_up(int x) {
tr[x].mx = x;
for (int i = 0; i < 2; i++) {
if (tr[tr[tr[x].s[i]].mx].v > tr[tr[x].mx].v) {
tr[x].mx = tr[tr[x].s[i]].mx;
}
}
}
void push_down(int x) {
if (tr[x].rev) {
rev(tr[x].s[0]), rev(tr[x].s[1]);
tr[x].rev = 0;
}
}
bool is_root(int x) {
return tr[tr[x].p].s[0] != x and tr[tr[x].p].s[1] != x;
}
void rotate(int x) {
int y = tr[x].p, z = tr[y].p;
int k = tr[y].s[1] == x;
if (!is_root(y)) tr[z].s[tr[z].s[1] == y] = x;
tr[x].p = z;
tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
tr[x].s[k ^ 1] = y; tr[y].p = x;
push_up(y), push_up(x);
}
void splay(int x) {
int top = 0, r = x;
stk[++top] = r;
while (!is_root(r)) stk[++top] = r = tr[r].p;
while (top)push_down(stk[top--]);
while (!is_root(x)) {
int y = tr[x].p, z = tr[y].p;
if (!is_root(y)) {
if ((tr[y].s[0] == x) ^ (tr[z].s[0] == y))rotate(x);
else rotate(y);
}
rotate(x);
}
}
void access(int x) {
int z = x;
for (int y = 0; x; y = x, x = tr[x].p) {
splay(x);
tr[x].s[1] = y, push_up(x);
}
splay(z);
}
void make_root(int x) {
access(x);
rev(x);
}
int find_root(int x) {
access(x);
while (tr[x].s[0])push_down(x), x = tr[x].s[0];
splay(x);
return x;
}
void split(int x, int y) {
make_root(x);
access(y);
}
void link(int x, int y) {
make_root(x);
if (find_root(y) != x) tr[x].p = y;
}
void cut(int x, int y) {
make_root(x);
if (find_root(y) == x and tr[y].p == x and !tr[y].s[0]) {
tr[x].s[1] = tr[y].p = 0;
push_up(x);
}
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
scanf("%d%d%d%d", &E[i].x, &E[i].y, &E[i].a, &E[i].b);
}
sort(E + 1, E + 1 + m);
for (int i = 1; i <= n + m; i++) {
fa[i] = i;
if (i > n) tr[i].v = E[i - n].b;
tr[i].mx = i;
}
int res = INF;
for (int i = 1; i <= m; i++) {
int x = E[i].x, y = E[i].y, a = E[i].a, b = E[i].b;
if (find(x) == find(y)) {
split(x, y);
int t = tr[y].mx;
if (tr[t].v > b) {
cut(E[t - n].x, t); cut(t, E[t - n].y);
link(x, n + i); link(n + i, y);
}
}
else {
fa[find(x)] = find(y);
link(x, n + i); link(n + i, y);
}
if (find(1) == find(n)) {
split(1, n);
res = min(res, a + tr[tr[n].mx].v);
}
}
if (res == INF)puts("-1");
else printf("%d\n", res);
}
6.11 左偏树
说是左偏树，其实叫可并堆更合理
对一个节点来说，它的左右子树的值都要大于它自己的值
定义距离 \(dis\) : 每个节点到空节点的距离
左偏树有一个重要的性质：
- 每个子树的左儿子的 \(dis\) 要大于等于 右儿子的 \(dis\) ，所以直觉上来说就是
“左偏”
- 插入 : \(O(log n)\)
- 求最小值： \(O(1)\)
- 删除最小值： \(O(log n)\)
- 合并两棵树： \(O(log n)\)
/*
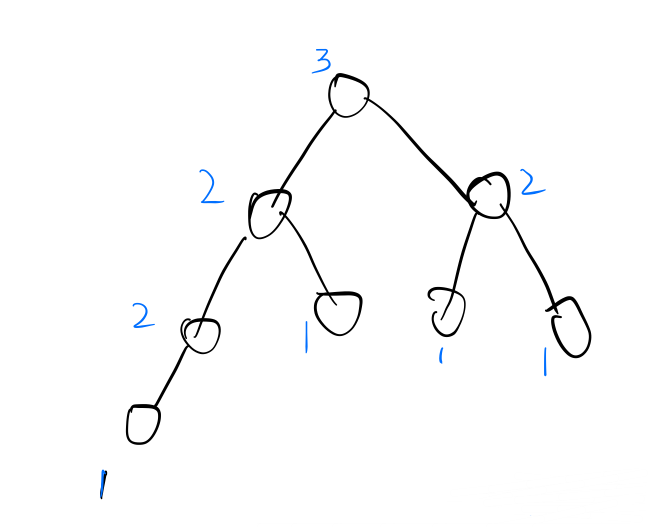
* @Author: zhl
* @Date: 2020-11-21 11:16:27
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int l[N], r[N], v[N], fa[N], idx, dis[N];
int find(int a) {
return a == fa[a] ? a : fa[a] = find(fa[a]);
}
bool cmp(int a, int b) {
if (v[a] != v[b])return v[a] < v[b];
return a < b;
}
int merge(int a, int b) {
if (!a or !b)return a + b;
if (cmp(b, a))swap(a, b);
r[a] = merge(r[a], b);
if (dis[r[a]] > dis[l[a]])swap(l[a], r[a]);
dis[a] = dis[r[a]] + 1;
return a;
}
int n;
int main() {
v[0] = 2e9;
scanf("%d", &n);
while (n--) {
int op, a, b;
scanf("%d%d", &op, &a);
if (op == 1) {
v[++idx] = a;
dis[idx] = 1;
fa[idx] = idx;
}
else if (op == 2) {
scanf("%d", &b);
a = find(a), b = find(b);
if (a != b) {
if (cmp(b, a)) swap(a, b);
fa[b] = a;
merge(a, b);
}
}
else if (op == 3) {
printf("%d\n", v[find(a)]);
}
else {
a = find(a);
if (cmp(r[a], l[a]))swap(l[a], r[a]);
fa[a] = l[a]; fa[l[a]] = l[a];
merge(l[a], r[a]);
}
}
}
6.12 ST表
/*
* @Author: zhl
* @LastEditTime: 2020-12-09 11:02:17
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int f[N][32];
int A[N];
int n, m, x, y;
void init() {
for (int i = 1; i <= n; i++) {
f[i][0] = A[i];
}
for (int j = 1; (1 << j) <= n; j++) {
for (int i = 1; i + (1 << j) - 1 <= n; i++) {
f[i][j] = max(f[i][j - 1], f[i + (1 << (j-1))][j - 1]);
}
}
}
int query(int l, int r) {
int k = log2(r - l + 1);
return max(f[l][k], f[r - (1 << k) + 1][k]);
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", A + i);
}
init();
for (int i = 1; i <= m; i++) {
scanf("%d%d", &x, &y);
printf("%d\n", query(x, y));
}
}
6.13 树链剖分
/*
* @Author: zhl
* @Date: 2020-10-13 20:36:59
*/
#include<bits/stdc++.h>
#define rep(i,a,b) for(int i = a;i <= b;i++)
#define repE(i,u) for(int i = head[u];i;i = E[i].next)
#define mid (l+r>>1)
#define lo (o<<1)
#define ro (o<<1|1)
using namespace std;
const int N = 4e5 + 10;
int A[N];
int n, m, root, mod;
struct Edge {
int to, next;
}E[N << 1];
int head[N], tot;
void addEdge(int from, int to) {
E[++tot] = Edge{ to,head[from] };
head[from] = tot++;
}
int fa[N], sz[N], Tfa[N], dep[N], son[N];
//dfs1处理dep,sz,fa,son(重儿子)
void dfs1(int u, int p) {
fa[u] = p;
dep[u] = dep[p] + 1;
sz[u] = 1;
int mx = -1;
repE(i, u) {
int v = E[i].to;
if (v == p)continue;
dfs1(v, u);
sz[u] += sz[v];
if (sz[v] > mx)mx = sz[v], son[u] = v;
}
}
int cnt;
int id[N], val[N], top[N];
//dfs2 剖分数链
void dfs2(int u, int topf) {
id[u] = ++cnt;
val[cnt] = A[u];
top[u] = topf;
if (!son[u])return;
dfs2(son[u], topf);
repE(i, u) {
int v = E[i].to;
if (v == fa[u] or v == son[u])continue;
dfs2(v, v);
}
}
int sum[N << 2], lz[N << 2];
int x, y, z;
void push_down(int o, int l, int r) {
if (!lz[o])return;
lz[lo] += lz[o];
lz[ro] += lz[o];
sum[lo] = (sum[lo] + lz[o] * (mid - l + 1)) % mod;
sum[ro] = (sum[ro] + lz[o] * (r - mid)) % mod;
lz[o] = 0;
}
void build(int o, int l, int r) {
if (l == r) {
sum[o] = val[l];
return;
}
build(lo, l, mid);
build(ro, mid + 1, r);
sum[o] += sum[lo] + sum[ro];
}
void updt(int o, int l, int r) {
if (x <= l and r <= y) {
lz[o] = (lz[o] + z) % mod;
sum[o] = (sum[o] + z * (r - l + 1)) % mod;
return;
}
push_down(o, l, r);
if (x <= mid)updt(lo, l, mid);
if (y > mid)updt(ro, mid + 1, r);
sum[o] = (sum[lo] + sum[ro]) % mod;
}
int query(int o, int l, int r) {
if (x <= l and r <= y) {
return sum[o];
}
int ans = 0;
push_down(o, l, r);
if (x <= mid)ans = (ans + query(lo, l, mid)) % mod;
if (y > mid)ans = (ans + query(ro, mid + 1, r)) % mod;
return ans;
}
int query_path(int a, int b) {
int ans = 0;
while (top[a] != top[b]) {
if (dep[top[a]] < dep[top[b]])swap(a, b);
x = id[top[a]]; y = id[a];
ans = (ans + query(1, 1, cnt)) % mod;
a = fa[top[a]];
}
if (dep[a] > dep[b])swap(a, b);
x = id[a]; y = id[b];
ans = (ans + query(1, 1, cnt)) % mod;
return ans;
}
void updt_path(int a, int b, int k) {
k %= mod;
while (top[a] != top[b]) {
if (dep[top[a]] < dep[top[b]])swap(a, b);
x = id[top[a]]; y = id[a]; z = k;
updt(1, 1, cnt);
a = fa[top[a]];
}
if (dep[a] > dep[b])swap(a, b);
x = id[a]; y = id[b]; z = k;
updt(1, 1, cnt);
}
int main() {
scanf("%d%d%d%d", &n, &m, &root, &mod);
for (int i = 1; i <= n; i++)scanf("%d", A + i);
for (int i = 1; i < n; i++) {
scanf("%d%d", &x, &y);
addEdge(x, y); addEdge(y, x);
}
dfs1(root, 0);
dfs2(root, root);
build(1, 1, cnt);
while (m--) {
int op; scanf("%d", &op);
int a, b, c;
if (op == 1) {//a,b 路径 + c
scanf("%d%d%d", &a, &b, &c);
updt_path(a, b, c);
}
if (op == 2) {//a,b 路径sum
scanf("%d%d", &a, &b);
printf("%d\n", query_path(a, b));
}
if (op == 3) {//a的subtree + c
scanf("%d%d", &a, &c);
x = id[a]; y = id[a] + sz[a] - 1;
z = c;
updt(1, 1, cnt);
}
if (op == 4) {
scanf("%d", &a);
x = id[a]; y = id[a] + sz[a] - 1;
printf("%d\n", query(1, 1, cnt));
}
}
}
/*
5 50 2 24000
7 3 7 8 0
1 2
1 5
3 1
4 1
*/
6.14 LCA
倍增法
#include<bits/stdc++.h>
#define repE(i,u) for(int i = head[u];i;i = E[i].next)
using namespace std;
const int N = 1e6 + 10;
int f[N][32];
int dep[N];
struct Edge {
int to, next;
}E[N << 1];
int head[N], tot;
void addEdge(int from, int to) {
E[++tot] = Edge{ to,head[from] };
head[from] = tot++;
}
void init(int u, int p) {
dep[u] = dep[p] + 1;
f[u][0] = p;
for (int x = 1; (1 << x) < dep[u]; x++) {
f[u][x] = f[f[u][x - 1]][x - 1];
}
repE(i, u) {
if (E[i].to == p)continue;
init(E[i].to, u);
}
}
int LCA(int x, int y) {
if (dep[x] < dep[y])swap(x, y);
while (dep[x] != dep[y]) {
int u = dep[x] - dep[y];
int v = 0;
while (!(u & (1 << v)))v++;
x = f[x][v];
}
while (x != y) {
int v = 0;
while (f[x][v] != f[y][v])v++;
x = f[x][max(0,v - 1)]; y = f[y][max(0,v - 1)];
}
return x;
}
int n, m, root;
int main() {
scanf("%d%d%d", &n, &m, &root);
for (int i = 1; i < n; i++) {
int x, y; scanf("%d%d", &x, &y);
addEdge(x, y);
addEdge(y, x);
}
init(root, 0);
for (int i = 1; i <= m; i++) {
int x, y; scanf("%d%d", &x, &y);
printf("%d\n", LCA(x, y));
}
}
树链剖分
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
struct Edge {
int to, next;
}E[N << 1];
int head[N], tot;
void addEdge(int from, int to) {
E[++tot] = Edge{ to,head[from] };
head[from] = tot;
}
int n, m, root;
int sz[N], son[N], top[N], dep[N], fa[N];
void dfs1(int u, int p) {
fa[u] = p; sz[u] = 1; dep[u] = dep[p] + 1;
for (int i = head[u]; i; i = E[i].next) {
int v = E[i].to;
if (v == p)continue;
dfs1(v, u);
sz[u] += sz[v];
if (sz[v] > sz[son[u]])son[u] = v;
}
}
void dfs2(int u, int tp) {
top[u] = tp;
if (son[u])dfs2(son[u], tp); else return;
for (int i = head[u]; i;i = E[i].next) {
int v = E[i].to;
if (v == fa[u] or v == son[u])continue;
dfs2(v, v);
}
}
int lca(int a, int b) {
while (top[a] != top[b]) {
if (dep[top[a]] < dep[top[b]])swap(a, b);
a = fa[top[a]];
}
if (dep[a] > dep[b])swap(a, b);
return a;
}
int main() {
scanf("%d%d%d", &n, &m, &root);
for (int i = 1; i < n; i++) {
int a, b; scanf("%d%d", &a, &b);
addEdge(a, b); addEdge(b, a);
}
dfs1(root, 0);
dfs2(root, root);
while (m--) {
int a, b; scanf("%d%d", &a, &b);
printf("%d\n", lca(a, b));
}
}
6.15 树上启发式合并
树上启发式合并 （ DSU on Tree) 是一种优雅的暴力
时间复杂度是 \(O(nlogn)\)
启发式就是基于直觉或经验的意思
树上启发式合并的代码很简单
void dfs(int u,int p,bool keep){
for(u.lightson v in u.son){
dfs(v,u,false);
}
if(have u.heavyson)dfs(u.heavyson,u,true);;
count(); //统计 u 及所有轻儿子的贡献，并计算 u 的答案
if(keep == false) del(); //如果不保留的话，删除记录
}
这段代码多看几遍，自己多想一想
对于当前的节点
u，在执行count()计算节点u的答案的时候，其所有子节点的答案都已经被计算出来，并且只有u的重儿子及其子树的记录没有被删除，所以计算u的答案的时候只要暴力遍历所有的轻儿子及其子树就可以。极其暴力（bushi
CF600E
首先要明白怎么统计答案
int mp[N],mx,sum; //mp是颜色出现次数，mx是最多出现的次数，sum是当前的最优节点的和
mp[color]++;
if (mp[color] > mx){
mx = mp[color];
sum = color;
}
else if (mp[color] == mx) sum += color;
然后就是开始暴力合并（启发式）
ll ans[N], sum, mx, mp[N];
void count(int u, int p,int hson) { //暴力算轻儿子及子树的答案，此时重儿子及其子树的信息还在。
mp[color[u]]++;
if (mp[color[u]] > mx) {
mx = mp[color[u]];
sum = color[u];
}
else if (mp[color[u]] == mx) sum += color[u];
repE(i, u) {
int v = E[i].to;
if (v == p or v == hson)continue;
count(v, u, hson);
}
}
void del(int u, int p) { //删除子树的信息。
mp[color[u]]--;
repE(i, u) {
int v = E[i].to;
if (v == p)continue;
del(v, u);
}
}
void dfs(int u, int p, bool keep) {
repE(i, u) {
int v = E[i].to;
if (v == p or v == son[u])continue;
dfs(v, u, false); //
}
if (son[u])dfs(son[u], u, true);
count(u, p, son[u]); ans[u] = sum;
if (not keep) {
sum = mx = 0;
del(u,p);
}
}
完整代码
#include<bits/stdc++.h>
#define repE(i,u) for(int i = head[u]; ~i;i = E[i].next)
using namespace std;
const int N = 1e5 + 10;
typedef long long ll;
int fa[N], sz[N], dep[N], son[N], color[N];
struct Edge { int to, next; }E[N << 1];
int head[N], tot;
void addEdge(int from, int to) { E[tot] = { to,head[from] }; head[from] = tot++; }
void dfs1(int u, int p) {
fa[u] = p;
dep[u] = dep[p] + 1;
sz[u] = 1;
int mx = -1;
repE(i, u) {
int v = E[i].to;
if (v == p)continue;
dfs1(v, u);
sz[u] += sz[v];
if (sz[v] > mx)mx = sz[v], son[u] = v;
}
}
ll ans[N], sum, mx, mp[N];
void count(int u, int p,int hson) {
mp[color[u]]++;
if (mp[color[u]] > mx) {
mx = mp[color[u]];
sum = color[u];
}
else if (mp[color[u]] == mx) sum += color[u];
repE(i, u) {
int v = E[i].to;
if (v == p or v == hson)continue;
count(v, u, hson);
}
}
void del(int u, int p) {
mp[color[u]]--;
repE(i, u) {
int v = E[i].to;
if (v == p)continue;
del(v, u);
}
}
void dfs(int u, int p, bool keep) {
repE(i, u) {
int v = E[i].to;
if (v == p or v == son[u])continue;
dfs(v, u, false);
}
if (son[u])dfs(son[u], u, true);
count(u, p, son[u]); ans[u] = sum;
if (not keep) {
sum = mx = 0;
del(u,p);
}
}
int n;
int main() {
ios::sync_with_stdio(0);
cin >> n; memset(head, -1, sizeof head);
for (int i = 1; i <= n; i++)cin >> color[i];
for (int i = 1; i < n; i++) {
int a, b; cin >> a >> b;
addEdge(a, b); addEdge(b, a);
}
dfs1(1, 0);
dfs(1, 0, true);
for (int i = 1; i <= n; i++)cout << ans[i] << " \n"[i == n];
}
七、图论
7.1 最短路
Dijkstra
/*
* @Author: zhl
* @LastEditTime: 2020-12-10 11:07:35
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, M = 1e6 + 10;
struct Edge {
int to, next, w;
}E[M];
int head[N], tot;
void addEdge(int from, int to, int w) {
E[tot] = Edge{ to,head[from],w };
head[from] = tot++;
}
void init() {
memset(head, -1, sizeof head);
}
int n, m, s;
int dis[N], vis[N];
typedef pair<int, int> p;
void Dijkstra() {
for (int i = 0; i <= n; i++)dis[i] = 0x7fffffff;
memset(vis, 0, sizeof vis);
priority_queue<p,vector<p>,greater<p>>Q;
Q.push({ 0,s }); dis[s] = 0;
while (not Q.empty()) {
int d = Q.top().first, u = Q.top().second; Q.pop();
if (vis[u])continue;
vis[u] = 1;
for (int i = head[u]; ~i; i = E[i].next) {
int v = E[i].to;
if (not vis[v] and dis[v] > d + E[i].w) {
dis[v] = dis[u] + E[i].w;
Q.push({ dis[v],v });
}
}
}
}
int main() {
init();
scanf("%d%d%d", &n, &m, &s);
for (int i = 1; i <= m; i++) {
int a, b, c; scanf("%d%d%d", &a, &b, &c);
addEdge(a, b, c);
}
Dijkstra();
for (int i = 1; i <= n; i++)printf("%d%c", dis[i], " \n"[i == n]);
}
vector版本
#include<bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10;
typedef pair<int, int> p;
vector<p>G[N];
int dis[N], vis[N], n, m, s;
void Dijkstra() {
for (int i = 0; i <= n; i++)dis[i] = 0x7fffffff;
dis[s] = 0;
priority_queue<p, vector<p>, greater<p>>Q;
Q.push({ 0,s });
while (not Q.empty()) {
int d = Q.top().first, u = Q.top().second; Q.pop();
if (vis[u])continue; vis[u] = 1;
for (p e : G[u]) {
if (not vis[e.first] and dis[e.first] > d + e.second) {
dis[e.first] = d + e.second;
Q.push({ dis[e.first],e.first });
}
}
}
}
int main() {
scanf("%d%d%d", &n, &m, &s);
for (int i = 0; i < m; i++) {
int a, b, c; scanf("%d%d%d", &a, &b, &c);
G[a].push_back({ b,c });
}
Dijkstra();
for (int i = 1; i <= n; i++)printf("%d%c", dis[i], " \n"[i == n]);
}
SPFA
#include<bits/stdc++.h>
#define to first
#define di second
using namespace std;
const int N = 1e5 + 10;
typedef pair<int, int> p;
vector<p>G[N];
int dis[N], inq[N], n, m, s;
deque<int>Q;
void slf() {
if (Q.size() > 2 and dis[Q.front()] > dis[Q.back()])swap(Q.front(), Q.back());
}
void spfa() {
memset(dis, 63, sizeof dis);
Q.push_back(s); inq[s] = 1; dis[s] = 0;
while (not Q.empty()) {
int u = Q.front(); Q.pop_front();
slf();
inq[u] = 0;
for (p e : G[u]) {
int v = e.to, d = e.di;
if (dis[v] > dis[u] + d) {
dis[v] = dis[u] + d;
if (not inq[v]) {
inq[v] = 1;
Q.push_back(v);
slf();
}
}
}
}
}
int main() {
scanf("%d%d%d", &n, &m, &s);
for (int i = 0; i < m; i++) {
int a, b, c; scanf("%d%d%d", &a, &b, &c);
G[a].push_back({ b,c });
}
spfa();
for (int i = 1; i <= n; i++) {
//cout << dis[i] << " \n"[i == n];
printf("%d%c", dis[i], " \n"[i == n]);
}
}
7.2 k短路
来自一年前的模板
#include<iostream>
#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn = 1e5 + 100;
struct E {
int to, w, next;
}Edgez[maxn], Edgef[maxn];
int headz[maxn], headf[maxn];
int cntz, cntf;
typedef pair<int, int> P;
int dis[maxn];
int vis[maxn];
int N, M;
struct Node {
int v, w;
bool operator < (const Node& a)const {
return w + dis[v] > a.w + dis[a.v];
}
};
void init() {
memset(headz, -1, sizeof(headz));
memset(headf, -1, sizeof(headf));
cntz = cntf = 0;
}
void addz(int from, int to, int w) {
Edgez[cntz] = E{ to,w,headz[from] };
headz[from] = cntz++;
}
void addf(int from, int to, int w) {
Edgef[cntf] = E{ to,w,headf[from] };
headf[from] = cntf++;
}
void dij(int s) {
memset(vis, 0, sizeof(vis));
memset(dis, 0x3f, sizeof(dis));
dis[s] = 0;
priority_queue<P, vector<P>, greater<P> >Q;
Q.push(pair<int,int>{ 0,s });
while (!Q.empty()) {
int u = Q.top().second;
Q.pop();
if (vis[u])continue;
vis[u] = 1;
for (int i = headf[u]; i != -1; i = Edgef[i].next) {
int v = Edgef[i].to;
if (dis[u] + Edgef[i].w < dis[v]) {
dis[v] = dis[u] + Edgef[i].w;;
Q.push(pair<int,int>{ dis[v],v });
}
}
}
}
int AStar(int s, int t, int k) {
if (dis[s] == 0x3f3f3f3f) {
return -1;
}
int cnt = 0;
priority_queue<Node>Q;
Q.push(Node{ s,0 });
while (!Q.empty()) {
Node tp = Q.top(); Q.pop();
if (tp.v == t) {
cnt++;
if (cnt == k) {
return tp.w;
}
}
for (int i = headz[tp.v]; i != -1; i = Edgez[i].next) {
Q.push(Node{ Edgez[i].to,Edgez[i].w + tp.w });
}
}
return -1;
}
int main() {
scanf("%d%d", &N, &M);
init();
for (int i = 1; i <= M; i++) {
int from, to, w;
scanf("%d%d%d", &from, &to, &w);
addz(from, to, w);
addf(to, from, w);
}
int s, t, k;
scanf("%d%d%d", &s, &t, &k);
dij(t);
if (s == t) {
k++;
}
cout << AStar(s, t, k) << endl;
}
7.3 网络流
1. 基本概念
流网络
\(G = (V,E)\)
有向图，一个源点，一个汇点。每条边都有一个属性（容量）。
不考虑反向边
可行流
可行流 \(f\) 需要满足
- 容量限制 （ \(0 \le f(u,v) \le c(u,v)\) )
- 流量守恒 （除了源点和汇点，其余点的流入等于流出）
\(|f|\) 表示可行流的流量
\[|f| = \sum_{(s,v)\in E} f(s,v) - \sum_{(s,v)\in E} f(v,s)
\]
最大流
指的是 最大可行流
残留网络
针对流网络的某一条流
记作 \(G_f\) ，是由流 \(f\) 决定的
\(V_f = V\) , \(E_f = E + E\) 的反向边
\[c'(u,v) = \begin{cases}c(u,v) - f(u,v) & (u,v)\in E\\f(u,v)\end{cases}
\]
残留网络 + 残留网络的一个可行流 = 原流网络的一个可行流
增广路径
在残留网络中从源点出发边权都大于0，到汇点结束的简单路径叫做增广路径。
- 增广路径一定是一个可行流
- 增广路径流量大于0
若对于一个可行流 \(f\) ,其 残留网络 \(G_f\) 若不存在增广路，则可以断定 \(f\) 是一个最大流
割
流网络 \(G = (V,E)\)
把点集 \(V\) 分成 \(S\), \(T\) , \(S \cap T = \empty\) , \(S \cup T = V\)
\(s \in S\) , \(t \in T\)
割的容量
所有从 \(S\) 到 \(T\) 的边的容量之和 \(c(S,T) = \sum_{u\in S} \sum_{v \in T} c(u,v)\)
最小割指割的容量的最小值
割的流量
\(f(S,T) = \sum_{u\in S}\sum_{v\in T}f(u,v) - \sum_{v\in T}\sum_{u\in S}f(v,u)\)
对任意的割，任意的一个可行流，割的流量一定小于等于割的容量
$\forall S,T \ \ \forall f , f(S,T) \le c(S,T) $
对任意的割，任意的可行流，一定有割的流量等于可行流的流量
\(\forall S,T\ \ \forall f \\|f| = f(S,T)\)
证明
首先有
\(f(S,T) = -f(T,S)\) , \(f(X,X)=0\)
\(f(S,X \cup Y) = f(S,X) + f(S,Y)\) , \(X \cap Y = \empty\)
\(f(X \cup Y, T) = f(X,T) + f(Y,T) , X \cap Y = \empty\)
\[f(S,T) = f(S,V) - f(S,S)\\=f(S,V)\\=f(s,V) + f(S-s,V)\\=f(s,V) =|f| \]
最大流最小割定理
- 流 \(f\) 是最大流
- 流 \(f\) 的残留网络中不存在增广路
- 存在某个割 \([S,T]\) , \(|f| = c(S,T)\)
三者相互等价
一推二和三推一都比较简单
- ①推②
反证，若存在增广路，则可以更大流量
- ③推①
最大流 \(\ge |f|\)
最大流 \(\le c(S,T) = |f|\)
所以 \(|f|\) = 最大流
最小割 \(\le c(S,T) = |f| \le\) 最大流
此时还有 最小割=最大流
- ②推③
\(S\) , 在 \(G_f\) 中，从 \(s\) 出发沿容量大于0的边走，所有能走到的点
\(T = V - S\) ,因为没有增广路，所以 \(S,T\) 是一个割
\(x\in S,y \in T\) , 有 \(f(x,y) = c(x,y)\) ,反向边 \(f(y,x) = 0\)
所以 \(|f| = c(S,T)\)
/*
* @Author: zhl
* @Date: 2020-10-20 11:09:59
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 2e6 + 10, M = 2e6 + 10, inf = 1e9;
int head[N],cur[N],dis[N],tot;
int n,m,s,t;
struct Edge{int to, next, flow;}E[M<<1];
void addEdge(int from,int to,int w){
E[tot] = {to,head[from],w};head[from] = tot++;
E[tot] = {from,head[to],0};head[to] = tot++;
}
bool bfs(){
queue<int>Q;memset(dis,-1,sizeof dis);
dis[s] = 0;cur[s] = head[s];Q.push(s);
while(!Q.empty()){
int u = Q.front();Q.pop();
for(int i = head[u];~i;i = E[i].next){
int v = E[i].to;
if(dis[v] == -1 and E[i].flow){
Q.push(v);dis[v] = dis[u] + 1;cur[v] = head[v];
if(v == t)return true;
}
}
}
return false;
}
int dfs(int u,int limit){
if(u == t)return limit;
int k,res = 0;
for(int i = cur[u]; ~i and res < limit;i = E[i].next){
int v = E[i].to;cur[u] = i;
if(dis[v] == dis[u] + 1 and E[i].flow){
k = dfs(v,min(E[i].flow,limit-res));
if(!k)dis[v] = -1;
E[i].flow -= k;E[i^1].flow += k;res += k;
}
}
return res;
}
int Dinic(){
int f,res = 0;
while(bfs())while(f=dfs(s,inf))res += f;
return res;
}
2. 基本算法
EK : \(O(nm^2)\)
Dinic: \(O(n^2m)\)
但其实上界非常宽松，一般 EK 能处理 \(10^3-10^4\) 的数据，Dinic \(10^4-10^5\)
EK算法
一般求最大流用不到，求最小费用流的时候 EK是核心算法
dinic
最大流
3.上下界流
无源汇上下界可行流
给有向图 G， 每条边都有一个流量上界和流量下界。若存在可行流，则输出每条边的流量，若不存在输出“NO“
思路：
对于每条边，先流下界，统计每个点的流量，所有点的流量和一定是0，建立一个超级源点连接所有流量为正的点，超级汇点连接流量为负的点，跑最大流，看能不能跑满流。因为所有流量为正的点表示有多，需要流出去，所以要连源点。
/*
* @Author: zhl
* @Date: 2020-10-20 11:09:59
*/
int val[N];
int minF[N];
signed main() {
scanf("%d%d", &n, &m);
memset(head, -1, sizeof(int) * (n + 10));
for (int i = 1; i <= m; i++) {
int a, b, c, d;
scanf("%d%d%d%d", &a, &b, &c, &d);
addEdge(a, b, d - c);
val[a] -= c;
val[b] += c;
minF[i - 1] = c;
}
int sum = 0;
for (int i = 1; i <= n; i++) {
if (val[i] > 0)addEdge(0, i, val[i]), sum += val[i];
if (val[i] < 0)addEdge(i, n + 1, -val[i]);
}
s = 0, t = n + 1;
int maxflow = Dinic();
if (maxflow == sum) {
printf("YES\n");
for (int i = 0; i < m; i++) {
printf("%d\n", E[(2*i)^1].flow + minF[i]);
}
}
else {
printf("NO\n");
}
}
有源汇上下界最大流
还是像无源汇上下界那样。
addEdge(t,s,inf) ，这么一加，然后跑一遍超级源点到超级汇点的可行流
加的这条边的反向边，就是一个 s 到 t 的基础流
然后再删掉这边，在此时的残留网络中跑一遍 s 到 t 的最大流
两个答案加起来就是 有源汇上下界最大流
/*
* @Author: zhl
* @Date: 2020-10-20 11:09:59
*/
#include<bits/stdc++.h>
//#define int long long
using namespace std;
const int N = 1e4 + 10, M = 1e5 + 10, inf = 1e9;
int n, m, s, t, tot, head[N];
int ans, dis[N], cur[N];
struct Edge {
int to, next, flow;
}E[M << 1];
void addEdge(int from, int to, int w) {
E[tot] = Edge{ to,head[from],w };
head[from] = tot++;
E[tot] = Edge{ from,head[to],0 };
head[to] = tot++;
}
int bfs() {
for (int i = 0; i <= n + 1; i++) dis[i] = -1;
queue<int>Q;
Q.push(s);
dis[s] = 0;
cur[s] = head[s];
while (!Q.empty()) {
int u = Q.front();
Q.pop();
for (int i = head[u]; ~i; i = E[i].next) {
int v = E[i].to;
if (E[i].flow && dis[v] == -1) {
Q.push(v);
dis[v] = dis[u] + 1;
cur[v] = head[v];
if (v == t)return 1; //分层成功
}
}
}
return 0;
}
int dfs(int x, int sum) {
if (x == t)return sum;
int k, res = 0;
for (int i = cur[x]; ~i && res < sum; i = E[i].next) {
cur[x] = i;
int v = E[i].to;
if (E[i].flow > 0 && (dis[v] == dis[x] + 1)) {
k = dfs(v, min(sum, E[i].flow));
if (k == 0) dis[v] = -1; //不可用
E[i].flow -= k; E[i ^ 1].flow += k;
res += k; sum -= k;
}
}
return res;
}
int Dinic() {
int ans = 0;
while (bfs()) {
ans += dfs(s, inf);
}
return ans;
}
int val[N];
int minF[N];
signed main() {
int S, T;
scanf("%d%d%d%d", &n, &m, &S, &T);
memset(head, -1, sizeof(int) * (n + 10));
for (int i = 1; i <= m; i++) {
int a, b, c, d;
scanf("%d%d%d%d", &a, &b, &c, &d);
addEdge(a, b, d - c);
val[a] -= c;
val[b] += c;
minF[i - 1] = c;
}
int sum = 0;
for (int i = 1; i <= n; i++) {
if (val[i] > 0)addEdge(0, i, val[i]), sum += val[i];
if (val[i] < 0)addEdge(i, n + 1, -val[i]);
}
s = 0, t = n + 1;
addEdge(T, S, inf);
int maxflow = Dinic();
if (maxflow == sum) {
int base = E[tot - 1].flow;
E[tot - 1].flow = E[tot - 2].flow = 0;
s = S; t = T;
printf("%d\n", base + Dinic());
}
else {
printf("No Solution\n");
}
}
有源汇上下界最小流
跟上面类似，跑
t到s的最大流，减去就可以了
/*
* @Author: zhl
* @Date: 2020-10-20 11:09:59
*/
#include<bits/stdc++.h>
//#define int long long
using namespace std;
const int N = 2e6 + 10, M = 2e6 + 10, inf = 1e9;
int n, m, s, t, tot, head[N];
int ans, dis[N], cur[N];
struct Edge {
int to, next, flow;
}E[M << 1];
void addEdge(int from, int to, int w) {
E[tot] = Edge{ to,head[from],w };
head[from] = tot++;
E[tot] = Edge{ from,head[to],0 };
head[to] = tot++;
}
int bfs() {
for (int i = 0; i <= n + 1; i++) dis[i] = -1;
queue<int>Q;
Q.push(s);
dis[s] = 0;
cur[s] = head[s];
while (!Q.empty()) {
int u = Q.front();
Q.pop();
for (int i = head[u]; ~i; i = E[i].next) {
int v = E[i].to;
if (E[i].flow && dis[v] == -1) {
Q.push(v);
dis[v] = dis[u] + 1;
cur[v] = head[v];
if (v == t)return 1; //分层成功
}
}
}
return 0;
}
int dfs(int x, int sum) {
if (x == t)return sum;
int k, res = 0;
for (int i = cur[x]; ~i && res < sum; i = E[i].next) {
cur[x] = i;
int v = E[i].to;
if (E[i].flow > 0 && (dis[v] == dis[x] + 1)) {
k = dfs(v, min(sum, E[i].flow));
if (k == 0) dis[v] = -1; //不可用
E[i].flow -= k; E[i ^ 1].flow += k;
res += k; sum -= k;
}
}
return res;
}
int Dinic() {
int ans = 0;
while (bfs()) {
ans += dfs(s, inf);
}
return ans;
}
int val[N];
int minF[N];
signed main() {
int S, T;
scanf("%d%d%d%d", &n, &m, &S, &T);
memset(head, -1, sizeof(int) * (n + 10));
for (int i = 1; i <= m; i++) {
int a, b, c, d;
scanf("%d%d%d%d", &a, &b, &c, &d);
addEdge(a, b, d - c);
val[a] -= c;
val[b] += c;
minF[i - 1] = c;
}
int sum = 0;
for (int i = 1; i <= n; i++) {
if (val[i] > 0)addEdge(0, i, val[i]), sum += val[i];
if (val[i] < 0)addEdge(i, n + 1, -val[i]);
}
s = 0, t = n + 1;
addEdge(T, S, inf);
int maxflow = Dinic();
if (maxflow == sum) {
int base = E[tot - 1].flow;
E[tot - 1].flow = E[tot - 2].flow = 0;
s = T; t = S;//只有这里改动了
printf("%d\n", base - Dinic());
}
else {
printf("No Solution\n");
}
}
4.最小割
最大权闭合子图
闭合子图
一个点集，不存在连接点集和点集外的边。
自闭集合，跟外界没有接触，边是自洽的。
最大权闭合子图
点权和最大的闭合子图
把闭合子图的集合映射到流网络的割的集合
原图 \(G(V,E)\)
建一个源点 \(s\) 到所有正权点，容量是点权，建一个汇点 \(t\) 到所有负权点，容量是点权绝对值。原图的所有边不变，容量 \(+\infty\)
原图 \(G\)
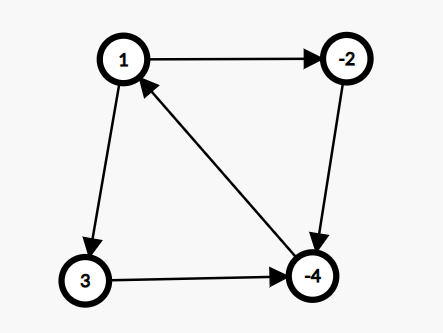
新图 \(G'\)
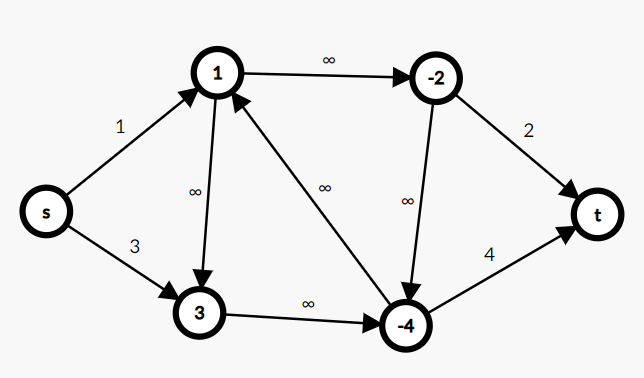
简单割
所有的割边都连接 \(s\) 或 \(t\)
简单割是一个很重要的概念。
现证明 简单割与闭合子图一一对应
对与闭合子图 \(V\) , $ V$ 中的点只能连接 \(s\) 或 \(t\) ,所以是简单割
对于一个简单割\([S,T]\) ，\(S-\{s\}\) 是一个闭合图，因为连接 \(S\) ，\(T\) 的边必定与 \(s\) 或 \(t\) 相连，所有 \(S-{s}\) 中的边只能连接自己
现在考虑数值上的关系
对于闭合子图 \(V\) , \(V^+\) 表示 \(V\) 中所有正权点的点权之和， \(V^-\) 表示所有负权的的点权绝对值之和
则 \(V\) 的权和为
\[s = V^+ - V^-
\]
现在考虑割 \([S,T]\) 的流量， \(S \to T\) 的只有两种边，一种是 \(V\) 到 \(t\) 的边，一种是 \(s\) 到 原图中除去 \(V\) 的其他点, 由于 \(s\) 连接的是正权的点，设原图所有正权点的点权之和是 \(sum\) ，则这部分正权点的点权之和是 \(sum - V^+\)
\[c = V^- + sum - V^+ = sum - s
\]
所以至此，要求最大权闭合子图，也就是求图 \(G'\) 的最小割
建基站需要花费 \(c_i\) , 用户需要 基站 \(a,b\) , 能获利 \(w_i\)
对于每个用户建立两条有向边代表若选了这个用户则这两个基站也要选，跑最大权闭合子图
/*
* @Author: zhl
* @Date: 2020-10-26 16:03:03
*/
#include<bits/stdc++.h>
#define rep(i,a,b) for(int i = a;i <= b;i++)
#define repE(i,u) for(int i = head[u];~i;i = E[i].next)
using namespace std;
const int N = 6e4 + 10, M = 2e5 + 10, inf = 1e8;
int head[N], cur[N], tot, dis[N];
int n, m, s, t;
struct Edge {
int to, next, flow;
}E[M << 1];
void addEdge(int from, int to, int w) {
//cout << from << " -> " << to << " : " << w << endl;
E[tot] = Edge{ to,head[from],w };
head[from] = tot++;
E[tot] = Edge{ from,head[to],0 };
head[to] = tot++;
}
bool bfs() {
memset(dis, -1, sizeof dis);
queue<int>Q; Q.push(s); cur[s] = head[s]; dis[s] = 0;
while (!Q.empty()) {
int u = Q.front(); Q.pop();
repE(i, u) {
int v = E[i].to;
if (dis[v] == -1 and E[i].flow) {
Q.push(v);
dis[v] = dis[u] + 1;
cur[v] = head[v];
if (v == t)return true;
}
}
}
return false;
}
int dfs(int u, int limit) {
if (u == t)return limit;
int k, res = 0;
for (int i = cur[u]; ~i and res < limit; i = E[i].next) {
int v = E[i].to;
cur[u] = i;
if (dis[v] == dis[u] + 1 and E[i].flow) {
k = dfs(v, min(E[i].flow, limit - res));
if (!k)dis[v] = -1;
E[i].flow -= k; E[i ^ 1].flow += k;
res += k;
}
}
return res;
}
int Dinic() {
int f, res = 0;
while (bfs())while (f = dfs(s, inf))res += f;
return res;
}
int val[N];
int main() {
scanf("%d%d", &n, &m);
memset(head, -1, sizeof head);
s = 0; t = n + m + 1;
rep(i, 1, n) {
scanf("%d", val + i);
addEdge(i, t, val[i]);
}
int sum = 0;
rep(i, 1, m) {
int a, b, c; scanf("%d%d%d", &a, &b, &c); sum += c;
val[n + i] = c; addEdge(n + i, a, inf); addEdge(n + i, b, inf);
addEdge(s, n + i, c);
}
printf("%d\n", sum - Dinic());
}
最大密度子图
参考
无向图 \(G(V,E)\) 的密度 \(D = \dfrac {|E|} {|V|}\)
若选择了边 \((u,v)\) 则必须有 \(u \in V , v \in V\)
最大密度子图
具有最大密度的子图，最大化 \(D' = \dfrac {|E'|} {|V'|}\)
根据之前的分数规划
可以二分答案
并且有如下引理
- 任意两个子图的密度差 \(\ge \dfrac 1{n^2}\)
\(\dfrac {m_1}{n_1} - \dfrac {m_2}{n_2} = \dfrac {m_1n_2 - m_2n_1} {n_1n_2} \ge \dfrac 1 {n_1n_2} \ge \dfrac 1 {n^2}\)
现在的主要问题是如何 \(Judge\)
设要检验的值为 \(g\) , 构造函数 $f = |E| - g|V| $ , 现在的目标是使得 \(f\) 最大
有两种方法
1. 最大权闭合子图
目标：
最大化 \(f = |E| - g|V|\)
把无向边 \((u,v)\) 看做一个点连接两条有向边指向 \(u\) 和 \(v\) 原图的点权值设为 \(-g\) ，
边的点为 \(1\) ,这样就转成了最大权闭合子图的问题
2.优化算法（诱导子图最小割）
对于点集 \(V'\) , 显然能选的边要尽可能的都选上
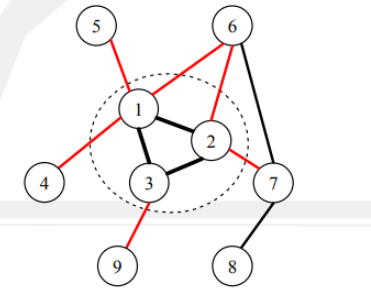
所有能选的边为 \(V'\) 中点的度的和减去割 \([V',\overline{V'}]\) 的容量的一半
\[|E'| = \dfrac {\sum_{v\in V'}deg(v) -c[V',\overline{V'}]}2
\]
\[f = \dfrac 12\big(\sum_{v\in V'}deg(v)-c[V',\overline{V'}] - 2\sum_{v \in V'}g\big) \\ = \dfrac 12\big(\sum_{v\in V'}(deg(v)-2g)-c[V',\overline{V'}] \big)
\]
按如下建图, \(U\) 是一个大常数，保证边权不是负数
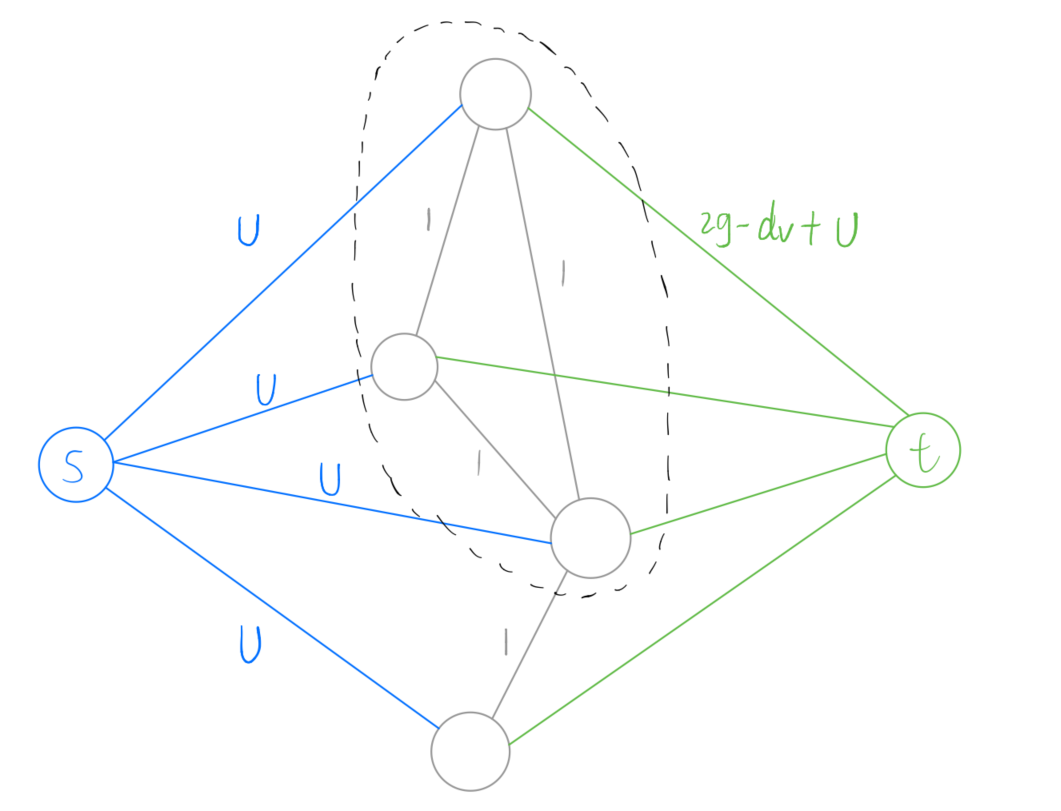
割 \([S,T]\) , \(S = {s} + V'\) ,\(T = {t} + \overline{V'}\)
割的容量 \(c[S,T]\) 有四个部分
\(s\to t\) ： \(0\)
\(s \to \overline{V'}\) : \(\sum_{v \in \overline{V'}}U\)
\(V' \to \overline{V'}\) ： 其实就是 \(c[V',\overline{V'}]\)
\(V' \to t\) ： \(\sum_{v\in V'}U+2g-d_v\)
\[c[S,T] = c[V',\overline{V'}] + Un + \sum_{v \in V'}2g-d_v = Un -2f
\]
所以最大化 \(f\) 即最小化 \(c[S,T]\) ，求最小割就可以了
5. 习题
说是模板，其实题意也不是那么简单易懂。
认真阅读题目后，建出下面的图
做完这个题可以更加理解 有源汇上下界最大流
源点全是出边，汇点全是入边会更好理解。
此时加的addEdge(t,s,inf) 的反向边的流量就是基础流量，然后去掉再跑最大流，两个流加起来。
左边的是 1-n 天， 右边是 1-m 个美少女
问题就是求 s 到 t 的有源汇上下界最大流
注意美少女的编号从 0 开始
/*
* @Author: zhl
* @Date: 2020-10-20 11:09:59
*/
#include<bits/stdc++.h>
//#define int long long
using namespace std;
const int N = 2e6 + 10, M = 2e6 + 10, inf = 1e9;
int n, m, s, t, tot, head[N];
int ans, dis[N], cur[N];
struct Edge {
int to, next, flow;
}E[M << 1];
void addEdge(int from, int to, int w) {
E[tot] = Edge{ to,head[from],w };
head[from] = tot++;
E[tot] = Edge{ from,head[to],0 };
head[to] = tot++;
}
int bfs() {
for (int i = 0; i <= n + m + 3; i++) dis[i] = -1;
queue<int>Q;
Q.push(s);
dis[s] = 0;
cur[s] = head[s];
while (!Q.empty()) {
int u = Q.front();
Q.pop();
for (int i = head[u]; ~i; i = E[i].next) {
int v = E[i].to;
if (E[i].flow && dis[v] == -1) {
Q.push(v);
dis[v] = dis[u] + 1;
cur[v] = head[v];
if (v == t)return 1; //分层成功
}
}
}
return 0;
}
int dfs(int x, int sum) {
if (x == t)return sum;
int k, res = 0;
for (int i = cur[x]; ~i && res < sum; i = E[i].next) {
cur[x] = i;
int v = E[i].to;
if (E[i].flow > 0 && (dis[v] == dis[x] + 1)) {
k = dfs(v, min(sum, E[i].flow));
if (k == 0) dis[v] = -1; //不可用
E[i].flow -= k; E[i ^ 1].flow += k;
res += k; sum -= k;
}
}
return res;
}
int Dinic() {
int ans = 0;
while (bfs()) {
ans += dfs(s, inf);
}
return ans;
}
int val[N];
int minF[N];
signed main() {
while(~scanf("%d%d",&n,&m)){
memset(head,-1,sizeof(int)*(n+m+10));
memset(val,0,sizeof(int)*(n+m+10));
tot = 0;
for(int i = 1;i <= m;i++){
int x;scanf("%d",&x);
addEdge(n+i,n+m+1,inf-x);
val[n+i]-=x;
val[n+m+1]+=x;
}
for(int i = 1;i <= n;i++){
int c,d;
scanf("%d%d",&c,&d);
addEdge(0,i,d);
val[0] -= 0;
val[i] += 0;
for(int j = 1;j <= c;j++){
int u,l,r;
scanf("%d%d%d",&u,&l,&r);
addEdge(i,u+n+1,r-l);
val[i] -= l;
val[u+n+1] += l;
}
}
s = n + m + 2;t = n + m + 3;
int sum = 0;
for(int i = 0;i <= n + m + 1;i++){
if(val[i] > 0){
addEdge(s,i,val[i]);
sum += val[i];
}
if(val[i] < 0)addEdge(i,t,-val[i]);
}
addEdge(n+m+1,0,inf);
int dd = Dinic();
//cout << dd << endl;
//cout << sum << endl;
if(dd == sum){
int res = E[tot-1].flow;
E[tot-1].flow = E[tot-2].flow = 0;
s = 0;t = n + m + 1;
printf("%d\n",res + Dinic());
}
else printf("-1\n");
puts("");
}
}
多源汇最大流
很简单，建一个超级源点连接所有的源点，建一个超级汇点连接所有的汇点。
/*
* @Author: zhl
* @Date: 2020-10-20 11:09:59
*/
#include<bits/stdc++.h>
#define rep(i,a,b) for(int i = a;i <= b;i++)
#define repE(i,u) for(int i = head[u];i;i = E[i].next)
//#define int long long
using namespace std;
const int N = 2e6 + 10, M = 2e6 + 10, inf = 1e9;
int n, m, s, t, tot, head[N];
int ans, dis[N], cur[N];
struct Edge {
int to, next, flow;
}E[M<<1];
void addEdge(int from, int to, int w) {
E[tot] = Edge{ to,head[from],w };
head[from] = tot++;
E[tot] = Edge{ from,head[to],0 };
head[to] = tot++;
}
int bfs() {
for (int i = 0; i <= n + 1; i++) dis[i] = -1;
queue<int>Q;
Q.push(s);
dis[s] = 0;
cur[s] = head[s];
while (!Q.empty()) {
int u = Q.front();
Q.pop();
for (int i = head[u]; ~i; i = E[i].next) {
int v = E[i].to;
if (E[i].flow && dis[v] == -1) {
Q.push(v);
dis[v] = dis[u] + 1;
cur[v] = head[v];
if (v == t)return 1; //分层成功
}
}
}
return 0;
}
int dfs(int x, int sum) {
if (x == t)return sum;
int k, res = 0;
for (int i = cur[x]; ~i && res < sum; i = E[i].next) {
cur[x] = i;
int v = E[i].to;
if (E[i].flow > 0 && (dis[v] == dis[x] + 1)) {
k = dfs(v, min(sum, E[i].flow));
if (k == 0) dis[v] = -1; //不可用
E[i].flow -= k;E[i ^ 1].flow += k;
res += k;sum -= k;
}
}
return res;
}
int Dinic() {
int ans = 0;
while (bfs()) {
ans += dfs(s,inf);
}
return ans;
}
signed main() {
scanf("%d%d%d%d",&n,&m,&s,&t);
memset(head, -1, sizeof(int) * (n + 10));
rep(i,1,s){
int x;scanf("%d",&x);
addEdge(0,x,inf);
}
rep(i,1,t){
int x;scanf("%d",&x);
addEdge(x,n+1,inf);
}
rep(i,1,m){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
addEdge(a,b,c);
}
s = 0,t = n + 1;
printf("%d\n",Dinic());
}
关键边
如果增加某一条边的容量可以增加最大流，则为关键边
跑一个最大流后，从源点bfs，从汇点bfs。交接处的边就是关键边
for (int i = 0; i < tot; i+=2) {
if (!E[i].flow and vis_t[E[i].to] and vis_s[E[i ^ 1].to]) ans++;
}
这里要 i+=2
/*
* @Author: zhl
* @Date: 2020-10-21 09:45:30
*/
#include<bits/stdc++.h>
#define rep(i,a,b) for(int i = a;i <= b;i++)
#define repE(i,u) for(int i = head[u];~i;i = E[i].next)
using namespace std;
const int N = 5e2 + 10, M = 5e3 + 10, inf = 1e9;
struct Edge {
int to, flow, next;
}E[M << 1];
int head[N], tot;
void addEdge(int from, int to, int w) {
E[tot] = Edge{ to,w,head[from] };
head[from] = tot++;
E[tot] = Edge{ from,0,head[to] };
head[to] = tot++;
}
int n, m, s, t;
int dis[N], cur[N];
bool bfs() {
rep(i, 0, n)dis[i] = -1;
queue<int>Q;
Q.push(s); dis[s] = 0; cur[s] = head[s];
while (!Q.empty()) {
int u = Q.front(); Q.pop();
repE(i, u) {
int v = E[i].to;
if (dis[v] == -1 and E[i].flow) {
cur[v] = head[v];
dis[v] = dis[u] + 1;
Q.push(v);
if (v == t)return true;
}
}
}
return false;
}
int dfs(int u, int limit) {
if (u == t)return limit;
int k, res = 0;
for (int i = cur[u]; ~i and res < limit; i = E[i].next) {
int v = E[i].to;
cur[u] = i;
if (dis[v] == dis[u] + 1 and E[i].flow) {
k = dfs(v, min(limit, E[i].flow));
if (k == 0)dis[v] = -1;
E[i].flow -= k; E[i ^ 1].flow += k;
limit -= k; res += k;
}
}
return res;
}
int Dinic() {
int res = 0;
while (bfs())res += dfs(s, inf);
return res;
}
int vis_s[N], vis_t[N];
void Dfs(int u, int* vis, int p) {
vis[u] = 1;
repE(i, u) {
int v = E[i].to;
if (!vis[v] and E[i ^ p].flow) {
Dfs(v, vis, p);
}
}
}
int main() {
scanf("%d%d", &n, &m);
memset(head, -1, sizeof head);
rep(i, 1, m) {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
addEdge(a + 1, b + 1, c);
}
s = 1, t = n;
Dinic();
Dfs(s, vis_s, 0); Dfs(t, vis_t, 1);
int ans = 0;
for (int i = 0; i < tot; i+=2) {
if (!E[i].flow and vis_t[E[i].to] and vis_s[E[i ^ 1].to]) {
ans++;
}
}
printf("%d\n", ans);
}
最大流判定
Poj 2455
\(N\) 个点 ， \(P\) 条双向边，每条边有长度，每条边只能走一次。
需要从 \(1\) 到 \(N\) ，进行 \(T\) 次。问经过的最大边权的最小值。
保证可以在不走重复道路的情况走 \(T\) 次
思路:
二分答案
判定用不超过 \(m\) 的边能不能到 \(T\) 次，跑网络流即可
/*
* @Author: zhl
* @Date: 2020-10-20 11:09:59
*/
#include<bits/stdc++.h>
#define rep(i,a,b) for(int i = a;i <= b;i++)
#define repE(i,u) for(int i = head[u];~i;i = E[i].next)
using namespace std;
const int N = 2e6 + 10, M = 2e6 + 10, inf = 1e9;
struct Edge {
int to, flow, next;
}E[M << 1];
int head[N], tot;
void addEdge(int from, int to, int w) {
E[tot] = Edge{ to,w,head[from] };
head[from] = tot++;
E[tot] = Edge{ from,0,head[to] };
head[to] = tot++;
}
int n, m, s, t, k;
int dis[N], cur[N];
bool bfs() {
rep(i, 0, n)dis[i] = -1;
queue<int>Q;
Q.push(s); dis[s] = 0; cur[s] = head[s];
while (!Q.empty()) {
int u = Q.front(); Q.pop();
repE(i, u) {
int v = E[i].to;
if (dis[v] == -1 and E[i].flow) {
cur[v] = head[v];
dis[v] = dis[u] + 1;
Q.push(v);
if (v == t)return true;
}
}
}
return false;
}
int dfs(int u, int limit) {
if (u == t)return limit;
int k, res = 0;
for (int i = cur[u]; ~i and res < limit; i = E[i].next) {
int v = E[i].to;
cur[u] = i;
if (dis[v] == dis[u] + 1 and E[i].flow) {
k = dfs(v, min(limit, E[i].flow));
if (k == 0)dis[v] = -1;
E[i].flow -= k; E[i ^ 1].flow += k;
limit -= k; res += k;
}
}
return res;
}
vector<pair<int, int> >G[300];
int Dinic() {
int res = 0;
while (bfs())res += dfs(s, inf);
return res;
}
bool judge(int m) {
memset(head, -1, sizeof(int) * (n + 10));
tot = 0;
for (int i = 1; i <= n; i++) {
for (auto e : G[i]) {
if (e.second <= m) {
addEdge(i, e.first, 1);
}
}
}
int maxflow = Dinic();
return maxflow >= k;
}
int main() {
scanf("%d%d%d", &n, &m, &k);
s = 1, t = n;
rep(i, 1, m) {
int a, b, c; scanf("%d%d%d", &a, &b, &c);
G[a].push_back({ b,c });
G[b].push_back({ a,c });
}
int l = 0, r = 1000100;
int ans = inf;
while (l <= r) {
int mid = l + r >> 1;
if (judge(mid)) {
ans = min(ans, mid);
r = mid - 1;
}
else {
l = mid + 1;
}
}
printf("%d\n", ans);
}
网络流24题
由于人类对自然资源的消耗，人们意识到大约在 2300 年之后，地球就不能再居住了。于是在月球上建立了新的绿地，以便在需要时移民。令人意想不到的是，2177 年冬由于未知的原因，地球环境发生了连锁崩溃，人类必须在最短的时间内迁往月球。
现有 \(n\) 个太空站位于地球与月球之间，且有 \(m\) 艘公共交通太空船在其间来回穿梭。每个太空站可容纳无限多的人，而太空船的容量是有限的，第 \(i\) 艘太空船只可容纳 \(h_i\) 个人。每艘太空船将周期性地停靠一系列的太空站，例如 \((1,3,4)\) 表示该太空船将周期性地停靠太空站 \(134134134\dots134134134\)…。每一艘太空船从一个太空站驶往任一太空站耗时均为 \(1\) 。人们只能在太空船停靠太空站(或月球、地球)时上、下船。
初始时所有人全在地球上，太空船全在初始站。试设计一个算法，找出让所有人尽快地全部转移到月球上的运输方案。
思路
按时间分层建图，停留的话就建一条垂直的
inf边（绿边）每一辆飞船按下图橙蓝建图，容量是载人数
/*
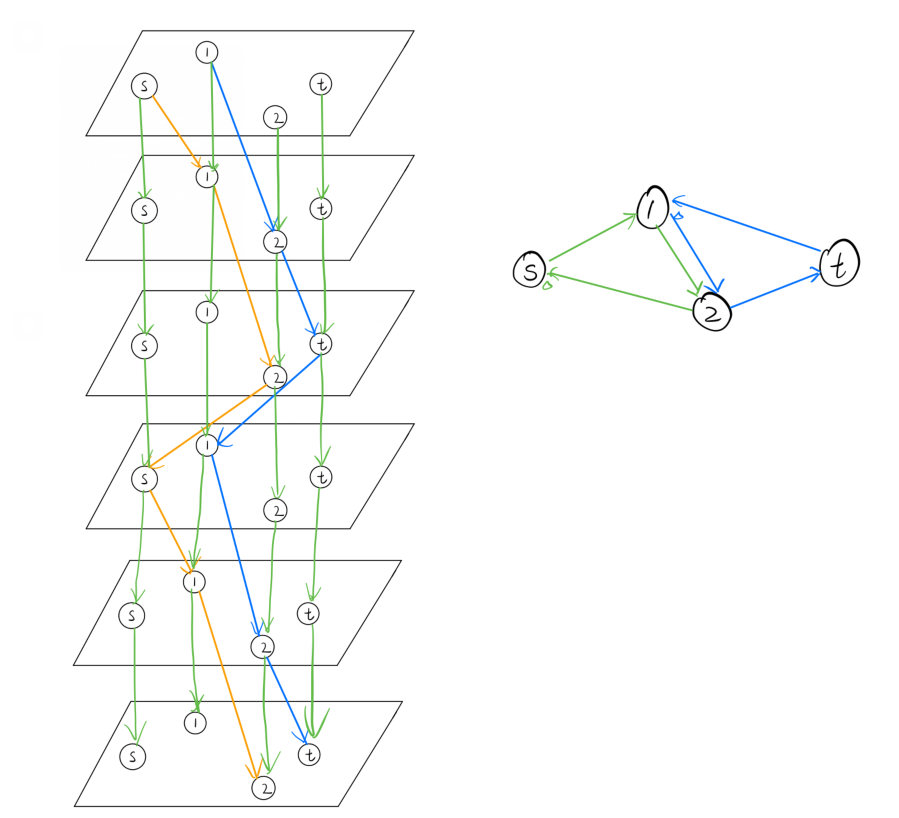
* @Author: zhl
* @Date: 2020-10-20 11:09:59
*/
#include<bits/stdc++.h>
#define rep(i,a,b) for(int i = a;i <= b;i++)
#define repE(i,u) for(int i = head[u];~i;i = E[i].next)
using namespace std;
const int N = 2e6 + 10, M = 2e6 + 10, inf = 1e9;
struct Edge {
int to, flow, next;
}E[M << 1];
int head[N], tot;
void addEdge(int from, int to, int w) {
E[tot] = Edge{ to,w,head[from] };
head[from] = tot++;
E[tot] = Edge{ from,0,head[to] };
head[to] = tot++;
}
int n, m, s, t, ans;
int dis[N], cur[N];
bool bfs() {
rep(i, 0, (n+2)*(ans+1))dis[i] = -1;
queue<int>Q;
Q.push(s); dis[s] = 0; cur[s] = head[s];
while (!Q.empty()) {
int u = Q.front(); Q.pop();
repE(i, u) {
int v = E[i].to;
if (dis[v] == -1 and E[i].flow) {
cur[v] = head[v];
dis[v] = dis[u] + 1;
Q.push(v);
if (v == t)return true;
}
}
}
return false;
}
int dfs(int u, int limit) {
if (u == t)return limit;
int k, res = 0;
for (int i = cur[u]; ~i and res < limit; i = E[i].next) {
int v = E[i].to;
cur[u] = i;
if (dis[v] == dis[u] + 1 and E[i].flow) {
k = dfs(v, min(limit, E[i].flow));
if (k == 0)dis[v] = -1;
E[i].flow -= k; E[i ^ 1].flow += k;
limit -= k; res += k;
}
}
return res;
}
int Dinic() {
int res = 0;
while (bfs())res += dfs(s, inf);
return res;
}
int H[N], k, r;
vector<int>G[30];
int fa[N];
int find(int a) { return a == fa[a] ? a : fa[a] = find(fa[a]); }
void merge(int a, int b) { if (find(a) != find(b))fa[find(a)] = find(b); }
int main() {
scanf("%d%d%d", &n, &m, &k);
rep(i, 0, n + 1)fa[i] = i;
rep(i, 1, m) {
scanf("%d%d", H + i, &r);
rep(j, 1, r) {
int x; scanf("%d", &x); if (x == -1)x = n + 1;
G[i].push_back(x);
}
rep(j, 1, r - 1) {
merge(G[i][0], G[i][j]);
}
}
if (find(0) != find(n + 1)){
printf("0\n");
return 0;
}
ans = 1;
while (1) {
memset(head, -1, sizeof(int)* ((n + 10)* (ans + 1)));
tot = 0;
rep(i, 0, ans - 1) {
rep(j, 1, m) {
int len = G[j].size();
int a = G[j][i % len] + (n + 2) * i;
int b = G[j][(i + 1) % len] + (n + 2) * (i + 1);
addEdge(a, b, H[j]);
}
rep(j, 0, n + 1) {
addEdge((n + 2) * i + j, (n + 2) * (i + 1) + j, inf);
}
}
s = 0, t = (n + 2) * (ans + 1) - 1;
if (Dinic() >= k) {
printf("%d\n", ans);
return 0;
}
ans++;
}
}
拆点
餐饮
农夫约翰一共烹制了 \(F\) 种食物，并提供了 \(D\) 种饮料。
约翰共有 \(N\) 头奶牛，其中第 \(i\) 头奶牛有 \(F_i\) 种喜欢的食物以及 \(D_i\) 种喜欢的饮料。
约翰需要给每头奶牛分配一种食物和一种饮料，并使得有吃有喝的奶牛数量尽可能大。
每种食物或饮料都只有一份，所以只能分配给一头奶牛食用（即，一旦将第 \(2\) 种食物分配给了一头奶牛，就不能再分配给其他奶牛了）。
开始想的错误思路是拆牛，超级源点连所有的牛
正解：
/*
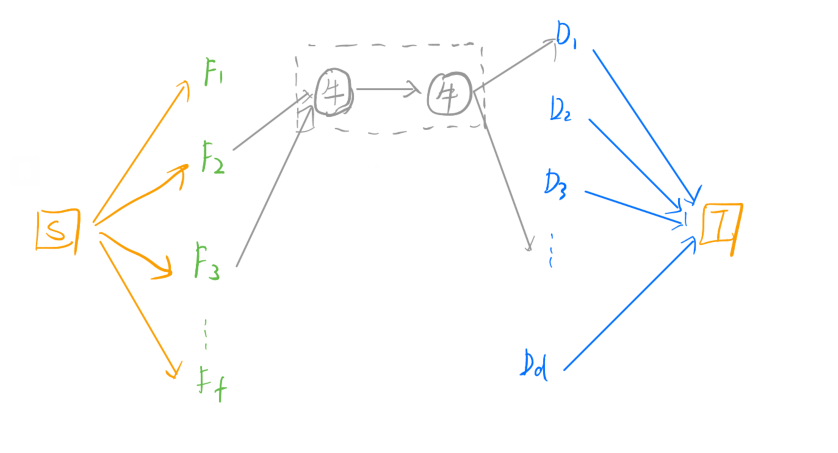
* @Author: zhl
* @Date: 2020-10-20 11:09:59
*/
/*
* 拆点策略： 把一头牛拆成两头，从源点到实物到牛再到饮料再到汇点
*/
#include<bits/stdc++.h>
#define rep(i,a,b) for(int i = a;i <= b;i++)
#define repE(i,u) for(int i = head[u];~i;i = E[i].next)
using namespace std;
const int N = 5e2 + 10, M = 5e3 + 10, inf = 1e9;
struct Edge {
int to, flow, next;
}E[M << 1];
int head[N], tot;
void addEdge(int from, int to, int w) {
E[tot] = Edge{ to,w,head[from] };
head[from] = tot++;
E[tot] = Edge{ from,0,head[to] };
head[to] = tot++;
}
int n, m, s, t, P_nums;//图中总点数[0-P_nums]
int dis[N], cur[N];
bool bfs() {
rep(i, 0, P_nums)dis[i] = -1;
queue<int>Q;
Q.push(s); dis[s] = 0; cur[s] = head[s];
while (!Q.empty()) {
int u = Q.front(); Q.pop();
repE(i, u) {
int v = E[i].to;
if (dis[v] == -1 and E[i].flow) {
cur[v] = head[v];
dis[v] = dis[u] + 1;
Q.push(v);
if (v == t)return true;
}
}
}
return false;
}
int dfs(int u, int limit) {
if (u == t)return limit;
int k, res = 0;
for (int i = cur[u]; ~i and res < limit; i = E[i].next) {
int v = E[i].to;
cur[u] = i;
if (dis[v] == dis[u] + 1 and E[i].flow) {
k = dfs(v, min(limit, E[i].flow));
if (k == 0)dis[v] = -1;
E[i].flow -= k; E[i ^ 1].flow += k;
limit -= k; res += k;
}
}
return res;
}
int Dinic() {
int res = 0;
while (bfs())res += dfs(s, inf);
return res;
}
int f, d;
int main() {
scanf("%d%d%d", &n, &f, &d);
P_nums = f + d + 2 * n + 1;
memset(head, -1, sizeof(int) * (P_nums + 10));
rep(i, 1, n) {
int u = f + d + 2 * (i - 1) + 1;
addEdge(u, u + 1, 1);
int a, b, x;
scanf("%d%d", &a, &b);
rep(j, 1, a) { scanf("%d", &x); addEdge(x, u, 1); }
rep(j, 1, b) { scanf("%d", &x); addEdge(u + 1, f + x, 1); }
}
rep(i, 1, f)addEdge(0, i, 1);
rep(i, f + 1, f + d)addEdge(i, P_nums, 1);
s = 0, t = P_nums;
printf("%d\n", Dinic());
}
给定正整数序列 \(x_1 \dots, x_n\)
- 计算其最长不下降子序列的长度 \(s\) 。
- 如果每个元素只允许使用一次，计算从给定的序列中最多可取出多少个长度为 \(s\) 的不下降子序列。
- 如果允许在取出的序列中多次使用 \(x_1\) 和 \(x_n\)（其他元素仍然只允许使用一次），则从给定序列中最多可取出多少个不同的长度为 \(s\) 的不下降子序列。
这里还是没有太吃透，有点朦胧
/*
* @Author: zhl
* @Date: 2020-10-21 15:19:08
*/
#include<bits/stdc++.h>
#define rep(i,a,b) for(int i = a;i <= b;i++)
#define repE(i,u) for(int i = head[u]; ~i; i = E[i].next)
using namespace std;
const int N = 1e4 + 10, M = 1e5 + 10, inf = 1e9;
struct Edge {
int to, next, flow;
}E[M << 1];
int head[N], tot;
void addEdge(int from, int to, int flow) {
E[tot] = Edge{ to,head[from],flow };
head[from] = tot++;
E[tot] = Edge{ from,head[to],0 };
head[to] = tot++;
}
int n, m, s, t, P_nums;
int dis[N], cur[N];
bool bfs() {
for (int i = 0; i <= P_nums; i++)dis[i] = -1;
queue<int>Q;
Q.push(s); cur[s] = head[s]; dis[s] = 0;
while (!Q.empty()) {
int u = Q.front(); Q.pop();
repE(i, u) {
int v = E[i].to;
if (dis[v] == -1 and E[i].flow) {
dis[v] = dis[u] + 1;
cur[v] = head[v];
Q.push(v);
if (v == t)return true;
}
}
}
return false;
}
int dfs(int u, int limit) {
if (u == t)return limit;
int k, res = 0;
for (int i = cur[u]; ~i and res < limit; i = E[i].next) {
cur[u] = i;
int v = E[i].to;
if (dis[v] == dis[u] + 1 and E[i].flow) {
k = dfs(v, min(limit, E[i].flow));
if (!k)dis[v] = -1;
E[i].flow -= k; E[i ^ 1].flow += k;
limit -= k; res += k;
}
}
return res;
}
int Dinic() {
int res = 0;
while (bfs())res += dfs(s, inf);
return res;
}
int f[N], A[N];
int main() {
scanf("%d", &n);
P_nums = 2 * n + 1;
s = 0, t = 2 * n + 1;
memset(head, -1, sizeof(int) * (2 * n + 100));
rep(i, 1, n)scanf("%d", A + i);
if(n == 1){
puts("1");puts("1");puts("1");
return 0;
}
for (int i = n; i >= 1; i--) {
f[i] = 1;
for (int j = n; j > i; j--) {
if (A[i] <= A[j]) {
f[i] = max(f[i], f[j] + 1);
}
}
}
int ans = 0;
rep(i, 1, n)ans = max(ans, f[i]);
printf("%d\n", ans);
rep(i, 1, n)addEdge(i, i + n, 1);
rep(i, 1, n) {
if (f[i] == ans)addEdge(0, i, 1);
if (f[i] == 1)addEdge(i + n, 2 * n + 1, 1);
}
rep(i, 1, n) {
rep(j, i + 1, n) {
if (A[j] >= A[i] and f[j] + 1 == f[i]) {
addEdge(i + n, j, 1);
}
}
}
printf("%d\n", Dinic());
memset(head, -1, sizeof(int) * (2 * n + 100));
tot = 0;
rep(i, 1, n)addEdge(i, i + n, 1);
rep(i, 1, n) {
if (f[i] == ans)addEdge(0, i, 1);
if (f[i] == 1)addEdge(i + n, 2 * n + 1, 1);
}
rep(i, 1, n) {
rep(j, i + 1, n) {
if (A[j] >= A[i] and f[j] + 1 == f[i]) {
addEdge(i + n, j, 1);
}
}
}
if(f[1] == ans){addEdge(0, 1, inf); addEdge(1, 1 + n, inf);}
if(f[n] == 1){addEdge(n, 2 * n, inf); addEdge(2 * n, 2 * n + 1, inf);}
printf("%d\n", Dinic());
}
企鹅旅行
在南极附近的某个地方，一些企鹅正站在一些浮冰上。
作为群居动物，企鹅们喜欢聚在一起，因此，它们想在同一块浮冰上会合。
企鹅们不想淋湿自己，所以它们只能利用自己有限的跳跃能力，在一块块浮冰之间跳跃移动，从而聚在一起。
但是，最近的温度很高，浮冰上也有了裂纹。
每当企鹅在一块浮冰上发力跳到另一块浮冰上时，起跳的浮冰都会遭到破坏，落点的浮冰并不会因此受到影响。
当浮冰被破坏到一定程度时，浮冰就会消失。
现在已知每块浮冰可以承受的具体起跳次数。
请帮助企鹅找出它们可以会合的所有浮冰。
/*
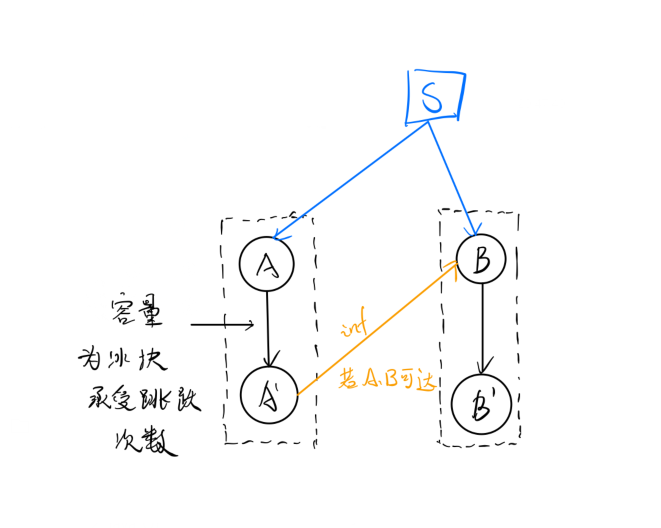
* @Author: zhl
* @Date: 2020-10-21 16:43:14
*/
#include<bits/stdc++.h>
#define rep(i,a,b) for(int i = a;i <= b;i++)
#define repE(i,u) for(int i = head[u];~i;i = E[i].next)
using namespace std;
const int N = 2e2 + 10, M = 2e6 + 10, inf = 1e9;
struct Edge {
int to, flow, next;
}E[M << 1];
int head[N], tot;
void addEdge(int from, int to, int w) {
E[tot] = Edge{ to,w,head[from] };
head[from] = tot++;
E[tot] = Edge{ from,0,head[to] };
head[to] = tot++;
}
int n, m, s, t, P_nums;//图中总点数[0-P_nums]
queue<int>Q;
int dis[N], cur[N];
bool bfs() {
rep(i, 0, P_nums)dis[i] = -1;
while (!Q.empty())Q.pop();
Q.push(s); dis[s] = 0; cur[s] = head[s];
while (!Q.empty()) {
int u = Q.front(); Q.pop();
repE(i, u) {
int v = E[i].to;
if (dis[v] == -1 and E[i].flow) {
cur[v] = head[v];
dis[v] = dis[u] + 1;
Q.push(v);
if (v == t)return true;
}
}
}
return false;
}
int dfs(int u, int limit) {
if (u == t)return limit;
int k, res = 0;
for (int i = cur[u]; ~i and res < limit; i = E[i].next) {
int v = E[i].to;
cur[u] = i;
if (dis[v] == dis[u] + 1 and E[i].flow) {
k = dfs(v, min(limit - res, E[i].flow));
if (k == 0)dis[v] = -1;
E[i].flow -= k; E[i ^ 1].flow += k;
res += k;
}
}
return res;
}
int Dinic() {
int res = 0, f;
while (bfs())while (f = dfs(s, inf)) res += f;
return res;
}
int T; double r;
int x[N], y[N], now[N], G[N];
int cal_dis(int i, int j) {
return 1.0 * (x[i] - x[j]) * (x[i] - x[j]) + (y[i] - y[j]) * (y[i] - y[j]);
}
int main() {
scanf("%d", &T);
while (T--) {
scanf("%d%lf", &n, &r);
memset(head, -1, sizeof head);
tot = 0;
P_nums = 2 * n;
int sum = 0;
rep(i, 1, n) {
scanf("%d%d%d%d", x + i, y + i, now + i, G + i); sum += now[i];
addEdge(i, i + n, G[i]); addEdge(0, i, now[i]);
}
rep(i, 1, n)
rep(j, i + 1, n) {
//if (i == j)continue;
double d = cal_dis(i, j);
if (1.0 * d <= r * r) addEdge(i + n, j, inf), addEdge(j + n, i, inf);
}
int cnt = 0;
rep(i, 1, n) {
s = 0, t = i;
for (int i = 0; i < tot; i += 2) { E[i].flow += E[i ^ 1].flow; E[i ^ 1].flow = 0; }
if (Dinic() == sum) {
if (cnt)printf(" ");
printf("%d", i - 1);
cnt++;
}
}
if (!cnt)printf("-1");
puts("");
}
}
这里有个很神奇的操作
for (int i = 0; i < tot; i += 2) {
E[i].flow += E[i ^ 1].flow;
E[i ^ 1].flow = 0;
}
可以重置边的状态，不需要重新建边
看完题目，我很熟练的建立了一个这样的毒瘤图
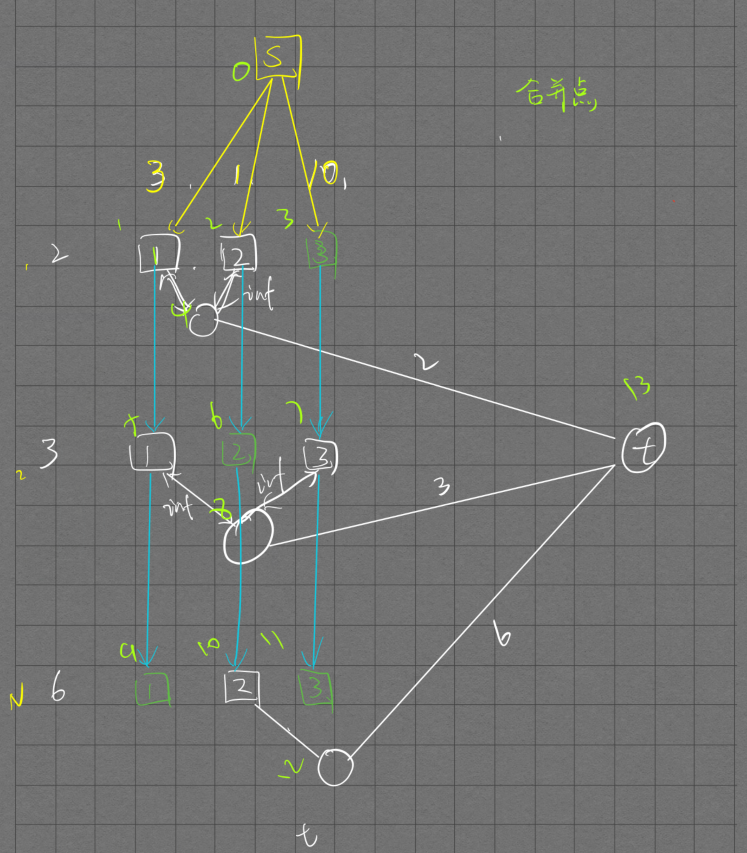
于是我快乐的 AC 了它。
int main() {
scanf("%d%d", &m, &n);
memset(head, -1, sizeof head);
rep(i, 1, m) { scanf("%d", &s); addEdge(0, i, s); }
s = 0, t = n * (m + 1) + 1;
rep(i, 1, n) {
int a, x;
scanf("%d", &a);
int base = (m + 1) * (i - 1);
int r = (m + 1) * i;
rep(j, 1, a) {
scanf("%d", &x);
addEdge(base + x, r, inf);
addEdge(r, base + x, inf);
}
scanf("%d", &x); addEdge(r, t, x);
if (i < n) {
rep(j, 1, m)addEdge(base + j, base + j + m + 1, inf);
}
}
printf("%d\n", Dinic());
}
但是，我眉头一皱，发现事情并不简单
\(5700ms\) ...
算了一下，大概有 \(n*(m+1)+1\) 这么多个点， \(1e5\) ... 边开了 \(1e6\) 才过
虽然说复杂度很宽松 , \(O(n^2m)\) ..
于是我看了一眼题解， 只有 \(n\) 个点
“在面对网络流问题时，如果一时想不出很好的构图方法，不如先构造一个最直观，或者说最“硬来”的模型，然后再用合并节点和边的方法来简直化这个模型。经过简化以后，好的构图思路自然就会涌现出来了。这是解决网络流问题的一个好方法。”
很显然我这个就是最原始的。
实际上这个图是可以合并的
可以把每一层的 $m + 1 $ 个点进行合并成一个点，记录下每个?圈之前的属主。
int main() {
scanf("%d%d", &m, &n);
memset(head, -1, sizeof head);
rep(i, 1, m) scanf("%d", w + i);
s = 0, t = n + 1;
rep(i, 1, n) {
int a, x;
scanf("%d", &a);
rep(j, 1, a) {
scanf("%d", &x);
if(!belong[x])addEdge(s,i,w[x]);
else addEdge(belong[x],i,inf);
belong[x] = i;
}
scanf("%d", &x); addEdge(i,t,x);
}
printf("%d\n", Dinic());
}
OJBK
真是美妙的建图
网络战争
给一个无向图 \(G=(V,E)\) ，求一个边集 \(C\) ，删除 \(C\) 后 \(s\) ，\(t\) 不再连通
最小化
\[\dfrac {\sum_{e\in C}w_e} {|C|}
\]
01分数规划
每个物品价值 \(w_i\) , 花费 \(c_i\)
选一些物品使得
\(\dfrac{\sum w} {\sum c}\) 最小
\[\dfrac {\sum w} {\sum c} < \lambda
\\ \sum w - \lambda \sum c < 0
\\ \sum_i (w_i - \lambda c_i) < 0
\]
至此，可以二分答案 \(\lambda\)
/*
* @Author: zhl
* @Date: 2020-10-22 15:44:57
*/
#include<bits/stdc++.h>
#define rep(i,a,b) for(int i = a;i <= b;i++)
#define repE(i,u) for(int i = head[u]; ~i; i = E[i].next)
using namespace std;
const int N = 2100, M = 10100, inf = 1e9;
struct Edge {
int to, next;
double flow;
}E[M << 1];
int head[N], tot;
void addEdge(int from, int to, double w) {
E[tot] = Edge{ to,head[from],w };
head[from] = tot++;
E[tot] = Edge{ from,head[to],0.0 };
head[to] = tot++;
}
int n, m, s, t;
queue<int>Q;
int dis[N], cur[N];
bool bfs() {
memset(dis, -1, sizeof dis);
while (!Q.empty())Q.pop();
Q.push(s); dis[s] = 0; cur[s] = head[s];
while (!Q.empty()) {
int u = Q.front(); Q.pop();
repE(i, u) {
int v = E[i].to;
if (dis[v] == -1 and E[i].flow) {
cur[v] = head[v];
dis[v] = dis[u] + 1;
Q.push(v);
if (v == t)return true;
}
}
}
return false;
}
double dfs(int u, double limit) {
if (u == t)return limit;
double k, res = 0;
for (int i = cur[u]; ~i and res < limit; i = E[i].next) {
int v = E[i].to;
cur[u] = i;
if (dis[v] == dis[u] + 1 and E[i].flow) {
k = dfs(v, min(limit - res, E[i].flow));
if (k == 0)dis[v] = -1;
E[i].flow -= k; E[i ^ 1].flow += k;
res += k;
}
}
return res;
}
double Dinic() {
double res = 0, f;
while (bfs())while (f = dfs(s, inf)) res += f;
return res;
}
const double eps = 1e-4;
int u[N],v[N],w[N];
bool judge(double x){
memset(head,-1,sizeof head);
tot = 0;
double sum = 0;
rep(i,1,m){
if(w[i] <= x) sum += w[i] - x;
else addEdge(u[i],v[i],w[i]-x),addEdge(v[i],u[i],w[i]-x);
}
return Dinic() + sum <= 0;
}
int main(){
scanf("%d%d%d%d",&n,&m,&s,&t);
rep(i,1,m){
scanf("%d%d%d",u+i,v+i,w+i);
}
double l = 0,r = 1e7;
while(r - l > eps){
double mid = (l + r) / 2;
if(judge(mid))r = mid;
else l = mid;
}
printf("%.2f\n",l);
}
给定一个无向图 \(G=(V,E)\) , 每个顶点都有一个标号，它是一个 \([0,2^{31}−1]\) 内的整数。
不同的顶点可能会有相同的标号。
对每条边 \((u,v)\) ，我们定义其费用 \(cost(u,v)\) 为 \(u\) 的标号与 \(v\) 的标号的异或值。
现在我们知道一些顶点的标号。
你需要确定余下顶点的标号使得所有边的费用和尽可能小。
每一个位其实都是独立的，* 表示没有权值，只要有一条路径从 1 到 0 就至少会产生 1 的贡献
void build(int xx) {
memset(head, -1, sizeof head);
tot = 0;
rep(i, 1, m) {
addEdge(x[i], y[i], 1);
addEdge(y[i], x[i], 1);
}
rep(i, 1, n) {
if (A[i] > 0) {
if ((A[i] >> xx) & 1) addEdge(i, t, inf);
else addEdge(s, i, inf);
}
}
}
int main() {
scanf("%d%d", &n, &m);
rep(i, 1, m) {
scanf("%d%d", x + i, y + i);
}
scanf("%d", &k);
memset(A, -1, sizeof A);
rep(i, 1, k) {
int a, x; scanf("%d%d", &a, &x);
A[a] = x;
}
long long ans = 0;
s = 0, t = n + 1;
rep(i, 0, 30) {
build(i);
ans += (1ll*Dinic() << i);
};
printf("%lld\n", ans);
}
7.4 MST
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int u[N], v[N], w[N], r[N], n, m, fa[N];
int find(int a) { return a == fa[a] ? a : fa[a] = find(fa[a]); }
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
scanf("%d%d%d", u + i, v + i, w + i); r[i] = fa[i] = i;
}
sort(r + 1, r + 1 + m, [&](int a, int b) {
return w[a] < w[b];
});
int cnt = 0; long long ans = 0;
for (int i = 1; i <= m; i++) {
int x = u[r[i]], y = v[r[i]], c = w[r[i]];
if (find(x) == find(y))continue;
x = find(x), y = find(y);
fa[x] = y; ans += c; if (++cnt == n - 1)break;
}
if (cnt != n - 1)puts("orz");
else printf("%lld\n", ans);
}
7.5 Tarjan
时间复杂度： \(O(n)\)
数组含义：
\(dfn[u]\) 时间戳，节点 \(u\) 的访问顺序
\(low[u]\) ， 从节点 \(u\) 出发能访问到的 \(dfn\) 最小的节点
求强连通分量
#include<bits/stdc++.h>
using namespace std;
const int N = 1e4 + 10;
vector<int>G[N];
int n, m;
int dfn[N], low[N], cnt, ans;
stack<int>stk;
void dfs(int u) {
dfn[u] = low[u] = ++cnt;
stk.push(u);
for (int v : G[u]) {
if (not dfn[v]) {
dfs(v);
}
low[u] = min(low[u], low[v]);
}
if (dfn[u] == low[u]) {
if (stk.top() != u)ans++;
while (stk.top() != u)stk.pop();
stk.pop();
}
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
cin >> n >> m;
for (int i = 0; i < m; i++) {
int a, b; cin >> a >> b; G[a].push_back(b);
}
for (int i = 1; i <= n; i++) {
if (!dfn[i])dfs(i);
}
cout << ans << endl;
}
割点
#include<bits/stdc++.h>
using namespace std;
const int N = 2e4 + 10;
vector<int>G[N];
int n, m;
int dfn[N], low[N], cnt, ans, cut[N];
stack<int>stk;
void dfs(int u,int rt) {
dfn[u] = low[u] = ++cnt;
stk.push(u); int ch = 0;
for (int v : G[u]) {
if (not dfn[v]) {
dfs(v, rt);
low[u] = min(low[u], low[v]);
if (low[v] >= dfn[u] and u != rt) cut[u] = 1;
if (u == rt)ch++;
}
else low[u] = min(low[u], dfn[v]);
}
if (ch > 1 and u == rt)cut[u] = 1;
}
int main() {
ios::sync_with_stdio(0); cin.tie(0);
cin >> n >> m;
for (int i = 0; i < m; i++) {
int a, b; cin >> a >> b;
G[a].push_back(b); G[b].push_back(a);
}
for (int i = 1; i <= n; i++) {
if (!dfn[i])dfs(i, i);
}
for (int i = 1; i <= n; i++)ans += cut[i];
cout << ans << endl;
for (int i = 1; i <= n; i++) {
if (cut[i])cout << i << " ";
}cout << endl;
}
缩点
#include<bits/stdc++.h>
using namespace std;
template<typename T = int>
inline const T read()
{
T x = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + ch - '0';
ch = getchar();
}
return x * f;
}
template<typename T>
inline void write(T x, bool ln)
{
if (x < 0) {
putchar('-');
x = -x;
}
if (x > 9) write(x / 10, false);
putchar(x % 10 + '0');
if (ln) putchar(10);
}
const int N = 1e4 + 10;
int n, m;
vector<int>G[N];
int w[N], dfn[N], low[N], cnt, vis[N], col[N];
int f[N], scnt;
stack<int>stk;
void dfs(int u) {
stk.push(u); vis[u] = 1;
dfn[u] = low[u] = ++cnt;
for (int v : G[u]) {
if (not dfn[v]) {
dfs(v);
low[u] = min(low[u], low[v]);
}
else if (vis[v]) low[u] = min(low[u], dfn[v]);
}
if (dfn[u] == low[u]) {
++scnt; int v;
do {
v = stk.top(); stk.pop();
vis[v] = 0;
col[v] = scnt;
f[scnt] += w[v];
} while (v != u);
}
}
int in[N], dp[N];
vector<int>g[N];
int main() {
n = read(),m = read();
for (int i = 1; i <= n; i++)w[i] = read();
for (int i = 1; i <= m; i++) {
int a = read(),b = read();
G[a].push_back(b);
}
for (int i = 1; i <= n; i++) {
if (not dfn[i])dfs(i);
}
for (int i = 1; i <= n; i++) {
int u = col[i];
for (int v : G[i]) {
int x = col[v];
if (x == u)continue;
g[u].push_back(x);
in[x]++;
}
}
queue<int>Q;
for (int i = 1; i <= scnt; i++) {
if (not in[i])Q.push(i);
dp[i] = f[i];
}
int ans = 0;
while (not Q.empty()) {
int u = Q.front(); Q.pop();
for (int v : g[u]) {
dp[v] = max(dp[v], f[v] + dp[u]);
in[v]--;
if (not in[v]) {
Q.push(v);
}
}
}
for (int i = 1; i <= scnt; i++) {
ans = max(ans, dp[i]);
}
printf("%d\n", ans);
}
八、计算几何
三点确认一个圆
最小圆覆盖
/*
* @Author: zhl
* @Date: 2020-11-25 15:24:24
*/
#include<bits/stdc++.h>
#define eps 1e-8
using namespace std;
struct point {
double x, y;
point operator + (const point& b)const {
return { x + b.x,y + b.y };
}
point operator / (const double b)const {
return { x / b,y / b };
}
}p[100005], o;
int n;
double r;
inline double sqr(double x) { return x * x; }
inline double dis(point a, point b){
return sqrt(sqr(a.x - b.x) + sqr(a.y - b.y));
}
inline bool cmp(double a, double b){
return fabs(a - b) < eps;
}
point geto(point a, point b, point c){
double a1, a2, b1, b2, c1, c2;
point ans;
a1 = 2 * (b.x - a.x), b1 = 2 * (b.y - a.y), c1 = sqr(b.x) - sqr(a.x) + sqr(b.y) - sqr(a.y);
a2 = 2 * (c.x - a.x), b2 = 2 * (c.y - a.y), c2 = sqr(c.x) - sqr(a.x) + sqr(c.y) - sqr(a.y);
if (cmp(a1, 0)){
ans.y = c1 / b1;
ans.x = (c2 - ans.y * b2) / a2;
}
else if (cmp(b1, 0)){
ans.x = c1 / a1;
ans.y = (c2 - ans.x * a2) / b2;
}
else{
ans.x = (c2 * b1 - c1 * b2) / (a2 * b1 - a1 * b2);
ans.y = (c2 * a1 - c1 * a2) / (b2 * a1 - b1 * a2);
}
return ans;
}
bool judge(point a) {
return dis(o, a) < r || cmp(dis(o, a), r);
}
int main(){
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%lf%lf", &p[i].x, &p[i].y);
random_shuffle(p + 1, p + 1 + n);
o = p[1];
for (int i = 1; i <= n; i++){
if (judge(p[i]))continue;
//o = (p[i] + p[1]) / 2; r = dis(p[i], p[1]) / 2;
o = p[i], r = 0;
for (int j = 1; j < i; j++){
if (judge(p[j]))continue;
o = (p[i] + p[j]) / 2; r = dis(p[i], p[j]) / 2;
for (int k = 1; k < j; k++){
if (judge(p[k]))continue;
o = geto(p[i], p[j], p[k]);
r = dis(o, p[i]);
}
}
}
printf("%.10lf\n%.10lf %.10lf", r, o.x, o.y);
}
求圆外两个点的最短距离
题意：
三维空间内存在一个球，给球外两个点，问这两个点的最短距离
思路：
只要判断线段与圆是否相交就可以
对于圆 \(O\) 外的两点 \(s,t\) , 线段 \(st\) 与圆 \(O\) 相交的条件为
\[\dfrac {\overrightarrow{st} *\overrightarrow{so}} {|st|} > \sqrt{|so|^2 - r^2} \ \ and \ \ \overrightarrow{to} *\overrightarrow{ts} > 0
\]
第一个条件确定的范围是粉色直线内的区域，但是灰色区域是不合法的
第二个条件是蓝色的圆之外的点，这样就是满足题意的区域了
平面最近点对
分治
/*
* @Author: zhl
* @LastEditTime: 2020-12-11 10:24:45
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
struct point{
double x, y;
void input(){
scanf("%lf%lf", &x, &y);
}
double dis(point b){
return sqrt((x - b.x) * (x - b.x) + (y - b.y) * (y - b.y));
}
}P[N], tmp[N];
int n;
double solve(int l,int r){
double ans = 1e20;
if (l == r)return ans;
if (l + 1 == r)return P[l].dis(P[r]);
int mid = l + r >> 1;
int cnt = 0;
ans = min(solve(l, mid), solve(mid + 1, r));
for(int i = l;i <= r;i++){
if (fabs(P[mid].x - P[i].x) <= ans)tmp[++cnt] = P[i];
}
sort(tmp + 1, tmp + 1 + cnt, [](point a, point b) {
return a.y < b.y;
});
for(int i = 1;i <= cnt;i++){
for(int j = i + 1;j <= cnt;j++){
if (fabs(tmp[i].y - tmp[j].y) > ans)continue;
ans = min(ans, tmp[i].dis(tmp[j]));
}
}
return ans;
}
int main(){
scanf("%d", &n);
for (int i = 1;i <= n;i++)P[i].input();
sort(P + 1, P + 1 + n, [](point a, point b) {
return a.x < b.x;
});
printf("%.4f\n", solve(1, n));
}
反演圆
D. Capture Stars
反演
定义
若 \(OP\cdot OP' = r^2\) , 则称 \(P\) 与 \(P'\) 关于 \(O\) 互为反演，反演半径为 \(r\)
该题反演后，转化为很简单的问题
#include<bits/stdc++.h>
using namespace std;
int T, n, R, r, cnt;
const int N = 1e4 + 10;
double x[N], y[N];
const double eps = 1e-8;
struct node {
double y;
int val;
bool operator < (const node& b)const {
return fabs(y - b.y) < eps ? val > b.val : y < b.y;
}
}A[N<<1];
void insert(int idx) {
double d = fabs(1.0 * R * R / r + R - x[idx]);
double dy = sqrt((1.0 * R * R / r - R) * (1.0 * R * R / r - R) - d * d);
A[cnt++] = { y[idx] + dy ,-1 };
A[cnt++] = { y[idx] - dy,1 };
}
int main() {
scanf("%d", &T);
while (T--) {
cnt = 0;
scanf("%d%d%d", &n, &R, &r);
for (int i = 0; i < n; i++) {
scanf("%lf%lf", x + i, y + i);
double dis = sqrt(x[i] * x[i] + y[i] * y[i]);
double t = 4 * R * R / (dis*dis);
x[i] *= t; y[i] *= t;
insert(i);
}
//x = R*R/r + R
int ans = 0, now = 0;
sort(A, A + cnt);
for (int i = 0; i < cnt; i++) {
now += A[i].val;
ans = max(ans, now);
}
printf("%d\n", ans);
}
}
kuangbin模板
/*
* @Author: zhl
* @LastEditTime: 2020-11-30 15:03:34
*/
// `计算几何模板`
#include<bits/stdc++.h>
using namespace std;
const double eps = 1e-8;
const double inf = 1e20;
const double pi = acos(-1.0);
const int maxp = 1010;
//`Compares a double to zero`
int sgn(double x){
if(fabs(x) < eps)return 0;
if(x < 0)return -1;
else return 1;
}
//square of a double
inline double sqr(double x){return x*x;}
/*
* Point
* Point() - Empty constructor
* Point(double _x,double _y) - constructor
* input() - double input
* output() - %.2f output
* operator == - compares x and y
* operator < - compares first by x, then by y
* operator - - return new Point after subtracting curresponging x and y
* operator ^ - cross product of 2d points
* operator * - dot product
* len() - gives length from origin
* len2() - gives square of length from origin
* distance(Point p) - gives distance from p
* operator + Point b - returns new Point after adding curresponging x and y
* operator * double k - returns new Point after multiplieing x and y by k
* operator / double k - returns new Point after divideing x and y by k
* rad(Point a,Point b)- returns the angle of Point a and Point b from this Point
* trunc(double r) - return Point that if truncated the distance from center to r
* rotleft() - returns 90 degree ccw rotated point
* rotright() - returns 90 degree cw rotated point
* rotate(Point p,double angle) - returns Point after rotateing the Point centering at p by angle radian ccw
*/
struct Point{
double x,y;
Point(){}
Point(double _x,double _y){
x = _x;
y = _y;
}
void input(){
scanf("%lf%lf",&x,&y);
}
void output(){
printf("%.2f %.2f\n",x,y);
}
bool operator == (Point b)const{
return sgn(x-b.x) == 0 && sgn(y-b.y) == 0;
}
bool operator < (Point b)const{
return sgn(x-b.x)== 0?sgn(y-b.y)<0:x<b.x;
}
Point operator -(const Point &b)const{
return Point(x-b.x,y-b.y);
}
//叉积
double operator ^(const Point &b)const{
return x*b.y - y*b.x;
}
//点积
double operator *(const Point &b)const{
return x*b.x + y*b.y;
}
//返回长度
double len(){
return hypot(x,y);//库函数
}
//返回长度的平方
double len2(){
return x*x + y*y;
}
//返回两点的距离
double distance(Point p){
return hypot(x-p.x,y-p.y);
}
Point operator +(const Point &b)const{
return Point(x+b.x,y+b.y);
}
Point operator *(const double &k)const{
return Point(x*k,y*k);
}
Point operator /(const double &k)const{
return Point(x/k,y/k);
}
//`计算pa 和 pb 的夹角`
//`就是求这个点看a,b 所成的夹角`
//`测试 LightOJ1203`
double rad(Point a,Point b){
Point p = *this;
return fabs(atan2( fabs((a-p)^(b-p)),(a-p)*(b-p) ));
}
//`化为长度为r的向量`
Point trunc(double r){
double l = len();
if(!sgn(l))return *this;
r /= l;
return Point(x*r,y*r);
}
//`逆时针旋转90度`
Point rotleft(){
return Point(-y,x);
}
//`顺时针旋转90度`
Point rotright(){
return Point(y,-x);
}
//`绕着p点逆时针旋转angle`
Point rotate(Point p,double angle){
Point v = (*this) - p;
double c = cos(angle), s = sin(angle);
return Point(p.x + v.x*c - v.y*s,p.y + v.x*s + v.y*c);
}
};
/*
* Stores two points
* Line() - Empty constructor
* Line(Point _s,Point _e) - Line through _s and _e
* operator == - checks if two points are same
* Line(Point p,double angle) - one end p , another end at angle degree
* Line(double a,double b,double c) - Line of equation ax + by + c = 0
* input() - inputs s and e
* adjust() - orders in such a way that s < e
* length() - distance of se
* angle() - return 0 <= angle < pi
* relation(Point p) - 3 if point is on line
* 1 if point on the left of line
* 2 if point on the right of line
* pointonseg(double p) - return true if point on segment
* parallel(Line v) - return true if they are parallel
* segcrossseg(Line v) - returns 0 if does not intersect
* returns 1 if non-standard intersection
* returns 2 if intersects
* linecrossseg(Line v) - line and seg
* linecrossline(Line v) - 0 if parallel
* 1 if coincides
* 2 if intersects
* crosspoint(Line v) - returns intersection point
* dispointtoline(Point p) - distance from point p to the line
* dispointtoseg(Point p) - distance from p to the segment
* dissegtoseg(Line v) - distance of two segment
* lineprog(Point p) - returns projected point p on se line
* symmetrypoint(Point p) - returns reflection point of p over se
*
*/
struct Line{
Point s,e;
Line(){}
Line(Point _s,Point _e){
s = _s;
e = _e;
}
bool operator ==(Line v){
return (s == v.s)&&(e == v.e);
}
//`根据一个点和倾斜角angle确定直线,0<=angle<pi`
Line(Point p,double angle){
s = p;
if(sgn(angle-pi/2) == 0){
e = (s + Point(0,1));
}
else{
e = (s + Point(1,tan(angle)));
}
}
//ax+by+c=0
Line(double a,double b,double c){
if(sgn(a) == 0){
s = Point(0,-c/b);
e = Point(1,-c/b);
}
else if(sgn(b) == 0){
s = Point(-c/a,0);
e = Point(-c/a,1);
}
else{
s = Point(0,-c/b);
e = Point(1,(-c-a)/b);
}
}
void input(){
s.input();
e.input();
}
void adjust(){
if(e < s)swap(s,e);
}
//求线段长度
double length(){
return s.distance(e);
}
//`返回直线倾斜角 0<=angle<pi`
double angle(){
double k = atan2(e.y-s.y,e.x-s.x);
if(sgn(k) < 0)k += pi;
if(sgn(k-pi) == 0)k -= pi;
return k;
}
//`点和直线关系`
//`1 在左侧`
//`2 在右侧`
//`3 在直线上`
int relation(Point p){
int c = sgn((p-s)^(e-s));
if(c < 0)return 1;
else if(c > 0)return 2;
else return 3;
}
// 点在线段上的判断
bool pointonseg(Point p){
return sgn((p-s)^(e-s)) == 0 && sgn((p-s)*(p-e)) <= 0;
}
//`两向量平行(对应直线平行或重合)`
bool parallel(Line v){
return sgn((e-s)^(v.e-v.s)) == 0;
}
//`两线段相交判断`
//`2 规范相交`
//`1 非规范相交`
//`0 不相交`
int segcrossseg(Line v){
int d1 = sgn((e-s)^(v.s-s));
int d2 = sgn((e-s)^(v.e-s));
int d3 = sgn((v.e-v.s)^(s-v.s));
int d4 = sgn((v.e-v.s)^(e-v.s));
if( (d1^d2)==-2 && (d3^d4)==-2 )return 2;
return (d1==0 && sgn((v.s-s)*(v.s-e))<=0) ||
(d2==0 && sgn((v.e-s)*(v.e-e))<=0) ||
(d3==0 && sgn((s-v.s)*(s-v.e))<=0) ||
(d4==0 && sgn((e-v.s)*(e-v.e))<=0);
}
//`直线和线段相交判断`
//`-*this line -v seg`
//`2 规范相交`
//`1 非规范相交`
//`0 不相交`
int linecrossseg(Line v){
int d1 = sgn((e-s)^(v.s-s));
int d2 = sgn((e-s)^(v.e-s));
if((d1^d2)==-2) return 2;
return (d1==0||d2==0);
}
//`两直线关系`
//`0 平行`
//`1 重合`
//`2 相交`
int linecrossline(Line v){
if((*this).parallel(v))
return v.relation(s)==3;
return 2;
}
//`求两直线的交点`
//`要保证两直线不平行或重合`
Point crosspoint(Line v){
double a1 = (v.e-v.s)^(s-v.s);
double a2 = (v.e-v.s)^(e-v.s);
return Point((s.x*a2-e.x*a1)/(a2-a1),(s.y*a2-e.y*a1)/(a2-a1));
}
//点到直线的距离
double dispointtoline(Point p){
return fabs((p-s)^(e-s))/length();
}
//点到线段的距离
double dispointtoseg(Point p){
if(sgn((p-s)*(e-s))<0 || sgn((p-e)*(s-e))<0)
return min(p.distance(s),p.distance(e));
return dispointtoline(p);
}
//`返回线段到线段的距离`
//`前提是两线段不相交，相交距离就是0了`
double dissegtoseg(Line v){
return min(min(dispointtoseg(v.s),dispointtoseg(v.e)),min(v.dispointtoseg(s),v.dispointtoseg(e)));
}
//`返回点p在直线上的投影`
Point lineprog(Point p){
return s + ( ((e-s)*((e-s)*(p-s)))/((e-s).len2()) );
}
//`返回点p关于直线的对称点`
Point symmetrypoint(Point p){
Point q = lineprog(p);
return Point(2*q.x-p.x,2*q.y-p.y);
}
};
//圆
struct circle{
Point p;//圆心
double r;//半径
circle(){}
circle(Point _p,double _r){
p = _p;
r = _r;
}
circle(double x,double y,double _r){
p = Point(x,y);
r = _r;
}
//`三角形的外接圆`
//`需要Point的+ / rotate() 以及Line的crosspoint()`
//`利用两条边的中垂线得到圆心`
//`测试：UVA12304`
circle(Point a,Point b,Point c){
Line u = Line((a+b)/2,((a+b)/2)+((b-a).rotleft()));
Line v = Line((b+c)/2,((b+c)/2)+((c-b).rotleft()));
p = u.crosspoint(v);
r = p.distance(a);
}
//`三角形的内切圆`
//`参数bool t没有作用，只是为了和上面外接圆函数区别`
//`测试：UVA12304`
circle(Point a,Point b,Point c,bool t){
Line u,v;
double m = atan2(b.y-a.y,b.x-a.x), n = atan2(c.y-a.y,c.x-a.x);
u.s = a;
u.e = u.s + Point(cos((n+m)/2),sin((n+m)/2));
v.s = b;
m = atan2(a.y-b.y,a.x-b.x) , n = atan2(c.y-b.y,c.x-b.x);
v.e = v.s + Point(cos((n+m)/2),sin((n+m)/2));
p = u.crosspoint(v);
r = Line(a,b).dispointtoseg(p);
}
//输入
void input(){
p.input();
scanf("%lf",&r);
}
//输出
void output(){
printf("%.2lf %.2lf %.2lf\n",p.x,p.y,r);
}
bool operator == (circle v){
return (p==v.p) && sgn(r-v.r)==0;
}
bool operator < (circle v)const{
return ((p<v.p)||((p==v.p)&&sgn(r-v.r)<0));
}
//面积
double area(){
return pi*r*r;
}
//周长
double circumference(){
return 2*pi*r;
}
//`点和圆的关系`
//`0 圆外`
//`1 圆上`
//`2 圆内`
int relation(Point b){
double dst = b.distance(p);
if(sgn(dst-r) < 0)return 2;
else if(sgn(dst-r)==0)return 1;
return 0;
}
//`线段和圆的关系`
//`比较的是圆心到线段的距离和半径的关系`
int relationseg(Line v){
double dst = v.dispointtoseg(p);
if(sgn(dst-r) < 0)return 2;
else if(sgn(dst-r) == 0)return 1;
return 0;
}
//`直线和圆的关系`
//`比较的是圆心到直线的距离和半径的关系`
int relationline(Line v){
double dst = v.dispointtoline(p);
if(sgn(dst-r) < 0)return 2;
else if(sgn(dst-r) == 0)return 1;
return 0;
}
//`两圆的关系`
//`5 相离`
//`4 外切`
//`3 相交`
//`2 内切`
//`1 内含`
//`需要Point的distance`
//`测试：UVA12304`
int relationcircle(circle v){
double d = p.distance(v.p);
if(sgn(d-r-v.r) > 0)return 5;
if(sgn(d-r-v.r) == 0)return 4;
double l = fabs(r-v.r);
if(sgn(d-r-v.r)<0 && sgn(d-l)>0)return 3;
if(sgn(d-l)==0)return 2;
if(sgn(d-l)<0)return 1;
}
//`求两个圆的交点，返回0表示没有交点，返回1是一个交点，2是两个交点`
//`需要relationcircle`
//`测试：UVA12304`
int pointcrosscircle(circle v,Point &p1,Point &p2){
int rel = relationcircle(v);
if(rel == 1 || rel == 5)return 0;
double d = p.distance(v.p);
double l = (d*d+r*r-v.r*v.r)/(2*d);
double h = sqrt(r*r-l*l);
Point tmp = p + (v.p-p).trunc(l);
p1 = tmp + ((v.p-p).rotleft().trunc(h));
p2 = tmp + ((v.p-p).rotright().trunc(h));
if(rel == 2 || rel == 4)
return 1;
return 2;
}
//`求直线和圆的交点，返回交点个数`
int pointcrossline(Line v,Point &p1,Point &p2){
if(!(*this).relationline(v))return 0;
Point a = v.lineprog(p);
double d = v.dispointtoline(p);
d = sqrt(r*r-d*d);
if(sgn(d) == 0){
p1 = a;
p2 = a;
return 1;
}
p1 = a + (v.e-v.s).trunc(d);
p2 = a - (v.e-v.s).trunc(d);
return 2;
}
//`得到过a,b两点，半径为r1的两个圆`
int gercircle(Point a,Point b,double r1,circle &c1,circle &c2){
circle x(a,r1),y(b,r1);
int t = x.pointcrosscircle(y,c1.p,c2.p);
if(!t)return 0;
c1.r = c2.r = r;
return t;
}
//`得到与直线u相切，过点q,半径为r1的圆`
//`测试：UVA12304`
int getcircle(Line u,Point q,double r1,circle &c1,circle &c2){
double dis = u.dispointtoline(q);
if(sgn(dis-r1*2)>0)return 0;
if(sgn(dis) == 0){
c1.p = q + ((u.e-u.s).rotleft().trunc(r1));
c2.p = q + ((u.e-u.s).rotright().trunc(r1));
c1.r = c2.r = r1;
return 2;
}
Line u1 = Line((u.s + (u.e-u.s).rotleft().trunc(r1)),(u.e + (u.e-u.s).rotleft().trunc(r1)));
Line u2 = Line((u.s + (u.e-u.s).rotright().trunc(r1)),(u.e + (u.e-u.s).rotright().trunc(r1)));
circle cc = circle(q,r1);
Point p1,p2;
if(!cc.pointcrossline(u1,p1,p2))cc.pointcrossline(u2,p1,p2);
c1 = circle(p1,r1);
if(p1 == p2){
c2 = c1;
return 1;
}
c2 = circle(p2,r1);
return 2;
}
//`同时与直线u,v相切，半径为r1的圆`
//`测试：UVA12304`
int getcircle(Line u,Line v,double r1,circle &c1,circle &c2,circle &c3,circle &c4){
if(u.parallel(v))return 0;//两直线平行
Line u1 = Line(u.s + (u.e-u.s).rotleft().trunc(r1),u.e + (u.e-u.s).rotleft().trunc(r1));
Line u2 = Line(u.s + (u.e-u.s).rotright().trunc(r1),u.e + (u.e-u.s).rotright().trunc(r1));
Line v1 = Line(v.s + (v.e-v.s).rotleft().trunc(r1),v.e + (v.e-v.s).rotleft().trunc(r1));
Line v2 = Line(v.s + (v.e-v.s).rotright().trunc(r1),v.e + (v.e-v.s).rotright().trunc(r1));
c1.r = c2.r = c3.r = c4.r = r1;
c1.p = u1.crosspoint(v1);
c2.p = u1.crosspoint(v2);
c3.p = u2.crosspoint(v1);
c4.p = u2.crosspoint(v2);
return 4;
}
//`同时与不相交圆cx,cy相切，半径为r1的圆`
//`测试：UVA12304`
int getcircle(circle cx,circle cy,double r1,circle &c1,circle &c2){
circle x(cx.p,r1+cx.r),y(cy.p,r1+cy.r);
int t = x.pointcrosscircle(y,c1.p,c2.p);
if(!t)return 0;
c1.r = c2.r = r1;
return t;
}
//`过一点作圆的切线(先判断点和圆的关系)`
//`测试：UVA12304`
int tangentline(Point q,Line &u,Line &v){
int x = relation(q);
if(x == 2)return 0;
if(x == 1){
u = Line(q,q + (q-p).rotleft());
v = u;
return 1;
}
double d = p.distance(q);
double l = r*r/d;
double h = sqrt(r*r-l*l);
u = Line(q,p + ((q-p).trunc(l) + (q-p).rotleft().trunc(h)));
v = Line(q,p + ((q-p).trunc(l) + (q-p).rotright().trunc(h)));
return 2;
}
//`求两圆相交的面积`
double areacircle(circle v){
int rel = relationcircle(v);
if(rel >= 4)return 0.0;
if(rel <= 2)return min(area(),v.area());
double d = p.distance(v.p);
double hf = (r+v.r+d)/2.0;
double ss = 2*sqrt(hf*(hf-r)*(hf-v.r)*(hf-d));
double a1 = acos((r*r+d*d-v.r*v.r)/(2.0*r*d));
a1 = a1*r*r;
double a2 = acos((v.r*v.r+d*d-r*r)/(2.0*v.r*d));
a2 = a2*v.r*v.r;
return a1+a2-ss;
}
//`求圆和三角形pab的相交面积`
//`测试：POJ3675 HDU3982 HDU2892`
double areatriangle(Point a,Point b){
if(sgn((p-a)^(p-b)) == 0)return 0.0;
Point q[5];
int len = 0;
q[len++] = a;
Line l(a,b);
Point p1,p2;
if(pointcrossline(l,q[1],q[2])==2){
if(sgn((a-q[1])*(b-q[1]))<0)q[len++] = q[1];
if(sgn((a-q[2])*(b-q[2]))<0)q[len++] = q[2];
}
q[len++] = b;
if(len == 4 && sgn((q[0]-q[1])*(q[2]-q[1]))>0)swap(q[1],q[2]);
double res = 0;
for(int i = 0;i < len-1;i++){
if(relation(q[i])==0||relation(q[i+1])==0){
double arg = p.rad(q[i],q[i+1]);
res += r*r*arg/2.0;
}
else{
res += fabs((q[i]-p)^(q[i+1]-p))/2.0;
}
}
return res;
}
};
/*
* n,p Line l for each side
* input(int _n) - inputs _n size polygon
* add(Point q) - adds a point at end of the list
* getline() - populates line array
* cmp - comparision in convex_hull order
* norm() - sorting in convex_hull order
* getconvex(polygon &convex) - returns convex hull in convex
* Graham(polygon &convex) - returns convex hull in convex
* isconvex() - checks if convex
* relationpoint(Point q) - returns 3 if q is a vertex
* 2 if on a side
* 1 if inside
* 0 if outside
* convexcut(Line u,polygon &po) - left side of u in po
* gercircumference() - returns side length
* getarea() - returns area
* getdir() - returns 0 for cw, 1 for ccw
* getbarycentre() - returns barycenter
*
*/
struct polygon{
int n;
Point p[maxp];
Line l[maxp];
void input(int _n){
n = _n;
for(int i = 0;i < n;i++)
p[i].input();
}
void add(Point q){
p[n++] = q;
}
void getline(){
for(int i = 0;i < n;i++){
l[i] = Line(p[i],p[(i+1)%n]);
}
}
struct cmp{
Point p;
cmp(const Point &p0){p = p0;}
bool operator()(const Point &aa,const Point &bb){
Point a = aa, b = bb;
int d = sgn((a-p)^(b-p));
if(d == 0){
return sgn(a.distance(p)-b.distance(p)) < 0;
}
return d > 0;
}
};
//`进行极角排序`
//`首先需要找到最左下角的点`
//`需要重载号好Point的 < 操作符(min函数要用) `
void norm(){
Point mi = p[0];
for(int i = 1;i < n;i++)mi = min(mi,p[i]);
sort(p,p+n,cmp(mi));
}
//`得到凸包`
//`得到的凸包里面的点编号是0$\sim$n-1的`
//`两种凸包的方法`
//`注意如果有影响，要特判下所有点共点，或者共线的特殊情况`
//`测试 LightOJ1203 LightOJ1239`
void getconvex(polygon &convex){
sort(p,p+n);
convex.n = n;
for(int i = 0;i < min(n,2);i++){
convex.p[i] = p[i];
}
if(convex.n == 2 && (convex.p[0] == convex.p[1]))convex.n--;//特判
if(n <= 2)return;
int &top = convex.n;
top = 1;
for(int i = 2;i < n;i++){
while(top && sgn((convex.p[top]-p[i])^(convex.p[top-1]-p[i])) <= 0)
top--;
convex.p[++top] = p[i];
}
int temp = top;
convex.p[++top] = p[n-2];
for(int i = n-3;i >= 0;i--){
while(top != temp && sgn((convex.p[top]-p[i])^(convex.p[top-1]-p[i])) <= 0)
top--;
convex.p[++top] = p[i];
}
if(convex.n == 2 && (convex.p[0] == convex.p[1]))convex.n--;//特判
convex.norm();//`原来得到的是顺时针的点，排序后逆时针`
}
//`得到凸包的另外一种方法`
//`测试 LightOJ1203 LightOJ1239`
void Graham(polygon &convex){
norm();
int &top = convex.n;
top = 0;
if(n == 1){
top = 1;
convex.p[0] = p[0];
return;
}
if(n == 2){
top = 2;
convex.p[0] = p[0];
convex.p[1] = p[1];
if(convex.p[0] == convex.p[1])top--;
return;
}
convex.p[0] = p[0];
convex.p[1] = p[1];
top = 2;
for(int i = 2;i < n;i++){
while( top > 1 && sgn((convex.p[top-1]-convex.p[top-2])^(p[i]-convex.p[top-2])) <= 0 )
top--;
convex.p[top++] = p[i];
}
if(convex.n == 2 && (convex.p[0] == convex.p[1]))convex.n--;//特判
}
//`判断是不是凸的`
bool isconvex(){
bool s[2];
memset(s,false,sizeof(s));
for(int i = 0;i < n;i++){
int j = (i+1)%n;
int k = (j+1)%n;
s[sgn((p[j]-p[i])^(p[k]-p[i]))+1] = true;
if(s[0] && s[2])return false;
}
return true;
}
//`判断点和任意多边形的关系`
//` 3 点上`
//` 2 边上`
//` 1 内部`
//` 0 外部`
int relationpoint(Point q){
for(int i = 0;i < n;i++){
if(p[i] == q)return 3;
}
getline();
for(int i = 0;i < n;i++){
if(l[i].pointonseg(q))return 2;
}
int cnt = 0;
for(int i = 0;i < n;i++){
int j = (i+1)%n;
int k = sgn((q-p[j])^(p[i]-p[j]));
int u = sgn(p[i].y-q.y);
int v = sgn(p[j].y-q.y);
if(k > 0 && u < 0 && v >= 0)cnt++;
if(k < 0 && v < 0 && u >= 0)cnt--;
}
return cnt != 0;
}
//`直线u切割凸多边形左侧`
//`注意直线方向`
//`测试：HDU3982`
void convexcut(Line u,polygon &po){
int &top = po.n;//注意引用
top = 0;
for(int i = 0;i < n;i++){
int d1 = sgn((u.e-u.s)^(p[i]-u.s));
int d2 = sgn((u.e-u.s)^(p[(i+1)%n]-u.s));
if(d1 >= 0)po.p[top++] = p[i];
if(d1*d2 < 0)po.p[top++] = u.crosspoint(Line(p[i],p[(i+1)%n]));
}
}
//`得到周长`
//`测试 LightOJ1239`
double getcircumference(){
double sum = 0;
for(int i = 0;i < n;i++){
sum += p[i].distance(p[(i+1)%n]);
}
return sum;
}
//`得到面积`
double getarea(){
double sum = 0;
for(int i = 0;i < n;i++){
sum += (p[i]^p[(i+1)%n]);
}
return fabs(sum)/2;
}
//`得到方向`
//` 1 表示逆时针，0表示顺时针`
bool getdir(){
double sum = 0;
for(int i = 0;i < n;i++)
sum += (p[i]^p[(i+1)%n]);
if(sgn(sum) > 0)return 1;
return 0;
}
//`得到重心`
Point getbarycentre(){
Point ret(0,0);
double area = 0;
for(int i = 1;i < n-1;i++){
double tmp = (p[i]-p[0])^(p[i+1]-p[0]);
if(sgn(tmp) == 0)continue;
area += tmp;
ret.x += (p[0].x+p[i].x+p[i+1].x)/3*tmp;
ret.y += (p[0].y+p[i].y+p[i+1].y)/3*tmp;
}
if(sgn(area)) ret = ret/area;
return ret;
}
//`多边形和圆交的面积`
//`测试：POJ3675 HDU3982 HDU2892`
double areacircle(circle c){
double ans = 0;
for(int i = 0;i < n;i++){
int j = (i+1)%n;
if(sgn( (p[j]-c.p)^(p[i]-c.p) ) >= 0)
ans += c.areatriangle(p[i],p[j]);
else ans -= c.areatriangle(p[i],p[j]);
}
return fabs(ans);
}
//`多边形和圆关系`
//` 2 圆完全在多边形内`
//` 1 圆在多边形里面，碰到了多边形边界`
//` 0 其它`
int relationcircle(circle c){
getline();
int x = 2;
if(relationpoint(c.p) != 1)return 0;//圆心不在内部
for(int i = 0;i < n;i++){
if(c.relationseg(l[i])==2)return 0;
if(c.relationseg(l[i])==1)x = 1;
}
return x;
}
};
//`AB X AC`
double cross(Point A,Point B,Point C){
return (B-A)^(C-A);
}
//`AB*AC`
double dot(Point A,Point B,Point C){
return (B-A)*(C-A);
}
//`最小矩形面积覆盖`
//` A 必须是凸包(而且是逆时针顺序)`
//` 测试 UVA 10173`
double minRectangleCover(polygon A){
//`要特判A.n < 3的情况`
if(A.n < 3)return 0.0;
A.p[A.n] = A.p[0];
double ans = -1;
int r = 1, p = 1, q;
for(int i = 0;i < A.n;i++){
//`卡出离边A.p[i] - A.p[i+1]最远的点`
while( sgn( cross(A.p[i],A.p[i+1],A.p[r+1]) - cross(A.p[i],A.p[i+1],A.p[r]) ) >= 0 )
r = (r+1)%A.n;
//`卡出A.p[i] - A.p[i+1]方向上正向n最远的点`
while(sgn( dot(A.p[i],A.p[i+1],A.p[p+1]) - dot(A.p[i],A.p[i+1],A.p[p]) ) >= 0 )
p = (p+1)%A.n;
if(i == 0)q = p;
//`卡出A.p[i] - A.p[i+1]方向上负向最远的点`
while(sgn(dot(A.p[i],A.p[i+1],A.p[q+1]) - dot(A.p[i],A.p[i+1],A.p[q])) <= 0)
q = (q+1)%A.n;
double d = (A.p[i] - A.p[i+1]).len2();
double tmp = cross(A.p[i],A.p[i+1],A.p[r]) *
(dot(A.p[i],A.p[i+1],A.p[p]) - dot(A.p[i],A.p[i+1],A.p[q]))/d;
if(ans < 0 || ans > tmp)ans = tmp;
}
return ans;
}
//`直线切凸多边形`
//`多边形是逆时针的，在q1q2的左侧`
//`测试:HDU3982`
vector<Point> convexCut(const vector<Point> &ps,Point q1,Point q2){
vector<Point>qs;
int n = ps.size();
for(int i = 0;i < n;i++){
Point p1 = ps[i], p2 = ps[(i+1)%n];
int d1 = sgn((q2-q1)^(p1-q1)), d2 = sgn((q2-q1)^(p2-q1));
if(d1 >= 0)
qs.push_back(p1);
if(d1 * d2 < 0)
qs.push_back(Line(p1,p2).crosspoint(Line(q1,q2)));
}
return qs;
}
//`半平面交`
//`测试 POJ3335 POJ1474 POJ1279`
//***************************
struct halfplane:public Line{
double angle;
halfplane(){}
//`表示向量s->e逆时针(左侧)的半平面`
halfplane(Point _s,Point _e){
s = _s;
e = _e;
}
halfplane(Line v){
s = v.s;
e = v.e;
}
void calcangle(){
angle = atan2(e.y-s.y,e.x-s.x);
}
bool operator <(const halfplane &b)const{
return angle < b.angle;
}
};
struct halfplanes{
int n;
halfplane hp[maxp];
Point p[maxp];
int que[maxp];
int st,ed;
void push(halfplane tmp){
hp[n++] = tmp;
}
//去重
void unique(){
int m = 1;
for(int i = 1;i < n;i++){
if(sgn(hp[i].angle-hp[i-1].angle) != 0)
hp[m++] = hp[i];
else if(sgn( (hp[m-1].e-hp[m-1].s)^(hp[i].s-hp[m-1].s) ) > 0)
hp[m-1] = hp[i];
}
n = m;
}
bool halfplaneinsert(){
for(int i = 0;i < n;i++)hp[i].calcangle();
sort(hp,hp+n);
unique();
que[st=0] = 0;
que[ed=1] = 1;
p[1] = hp[0].crosspoint(hp[1]);
for(int i = 2;i < n;i++){
while(st<ed && sgn((hp[i].e-hp[i].s)^(p[ed]-hp[i].s))<0)ed--;
while(st<ed && sgn((hp[i].e-hp[i].s)^(p[st+1]-hp[i].s))<0)st++;
que[++ed] = i;
if(hp[i].parallel(hp[que[ed-1]]))return false;
p[ed]=hp[i].crosspoint(hp[que[ed-1]]);
}
while(st<ed && sgn((hp[que[st]].e-hp[que[st]].s)^(p[ed]-hp[que[st]].s))<0)ed--;
while(st<ed && sgn((hp[que[ed]].e-hp[que[ed]].s)^(p[st+1]-hp[que[ed]].s))<0)st++;
if(st+1>=ed)return false;
return true;
}
//`得到最后半平面交得到的凸多边形`
//`需要先调用halfplaneinsert() 且返回true`
void getconvex(polygon &con){
p[st] = hp[que[st]].crosspoint(hp[que[ed]]);
con.n = ed-st+1;
for(int j = st,i = 0;j <= ed;i++,j++)
con.p[i] = p[j];
}
};
//***************************
const int maxn = 1010;
struct circles{
circle c[maxn];
double ans[maxn];//`ans[i]表示被覆盖了i次的面积`
double pre[maxn];
int n;
circles(){}
void add(circle cc){
c[n++] = cc;
}
//`x包含在y中`
bool inner(circle x,circle y){
if(x.relationcircle(y) != 1)return 0;
return sgn(x.r-y.r)<=0?1:0;
}
//圆的面积并去掉内含的圆
void init_or(){
bool mark[maxn] = {0};
int i,j,k=0;
for(i = 0;i < n;i++){
for(j = 0;j < n;j++)
if(i != j && !mark[j]){
if( (c[i]==c[j])||inner(c[i],c[j]) )break;
}
if(j < n)mark[i] = 1;
}
for(i = 0;i < n;i++)
if(!mark[i])
c[k++] = c[i];
n = k;
}
//`圆的面积交去掉内含的圆`
void init_add(){
int i,j,k;
bool mark[maxn] = {0};
for(i = 0;i < n;i++){
for(j = 0;j < n;j++)
if(i != j && !mark[j]){
if( (c[i]==c[j])||inner(c[j],c[i]) )break;
}
if(j < n)mark[i] = 1;
}
for(i = 0;i < n;i++)
if(!mark[i])
c[k++] = c[i];
n = k;
}
//`半径为r的圆，弧度为th对应的弓形的面积`
double areaarc(double th,double r){
return 0.5*r*r*(th-sin(th));
}
//`测试SPOJVCIRCLES SPOJCIRUT`
//`SPOJVCIRCLES求n个圆并的面积，需要加上init\_or()去掉重复圆（否则WA）`
//`SPOJCIRUT 是求被覆盖k次的面积，不能加init\_or()`
//`对于求覆盖多少次面积的问题，不能解决相同圆，而且不能init\_or()`
//`求多圆面积并，需要init\_or,其中一个目的就是去掉相同圆`
void getarea(){
memset(ans,0,sizeof(ans));
vector<pair<double,int> >v;
for(int i = 0;i < n;i++){
v.clear();
v.push_back(make_pair(-pi,1));
v.push_back(make_pair(pi,-1));
for(int j = 0;j < n;j++)
if(i != j){
Point q = (c[j].p - c[i].p);
double ab = q.len(),ac = c[i].r, bc = c[j].r;
if(sgn(ab+ac-bc)<=0){
v.push_back(make_pair(-pi,1));
v.push_back(make_pair(pi,-1));
continue;
}
if(sgn(ab+bc-ac)<=0)continue;
if(sgn(ab-ac-bc)>0)continue;
double th = atan2(q.y,q.x), fai = acos((ac*ac+ab*ab-bc*bc)/(2.0*ac*ab));
double a0 = th-fai;
if(sgn(a0+pi)<0)a0+=2*pi;
double a1 = th+fai;
if(sgn(a1-pi)>0)a1-=2*pi;
if(sgn(a0-a1)>0){
v.push_back(make_pair(a0,1));
v.push_back(make_pair(pi,-1));
v.push_back(make_pair(-pi,1));
v.push_back(make_pair(a1,-1));
}
else{
v.push_back(make_pair(a0,1));
v.push_back(make_pair(a1,-1));
}
}
sort(v.begin(),v.end());
int cur = 0;
for(int j = 0;j < v.size();j++){
if(cur && sgn(v[j].first-pre[cur])){
ans[cur] += areaarc(v[j].first-pre[cur],c[i].r);
ans[cur] += 0.5*(Point(c[i].p.x+c[i].r*cos(pre[cur]),c[i].p.y+c[i].r*sin(pre[cur]))^Point(c[i].p.x+c[i].r*cos(v[j].first),c[i].p.y+c[i].r*sin(v[j].first)));
}
cur += v[j].second;
pre[cur] = v[j].first;
}
}
for(int i = 1;i < n;i++)
ans[i] -= ans[i+1];
}
};
