数论基础知识复习





数论知识点 - 庄昊霖 - 博客园 (cnblogs.com)
一、 迪利克雷卷积
首先记住三个完全积性函数
\[id(n)\ = \ n \\
I(n)\ = \ 1 \\
\epsilon(n) \ = \ [\ n==1\ ]
\]
元函数 \(\epsilon\) 是迪利克雷卷积的单位
定义迪利克雷卷积
\[f*g \ (n) = \sum_{d|n}f(d)g(\dfrac n d)
\]
满足交换律,分配律,结合律
\[d(n) = \sum_{d|n} 1 = I*I \\
\sigma(n) = \sum_{d|n}d = id*I
\]
莫比乌斯函数有个性质
\[u*I = \sum_{d|n}\mu(d) = \epsilon = [n == 1]
\]
设
\[n = p_1^{a_1}p_2^{a_2}...p_k^{a_k}
\]
\[\sum_{d|n}\mu(d)=\sum_{i=0}^k(-1)^iC_k^i=[n==1]
\]
二、 莫比乌斯反演
I:
\[F(n) = \sum_{d|n}f(d) \to f(n)=\sum_{d|n}\mu(d)F(\dfrac nd)
\]
II:
\[F(n)=\sum_{n|d}f(d) \to f(n) = \sum_{n|d}\mu(\dfrac dn)F(d)
\]
三、 杜教筛
设
\[h = f * g
\]
记 \(S(n) = \sum_{i=1}^{n}f(i)\)
\[\sum_{i=1}^{n}h(i)=\sum_{i=1}^{n}\sum_{d|i}g(d)\cdot f(\frac{i}{d})\\\to =\sum_{d=1}^{n}g(d)\cdot\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}f({i})
\]
\[\to \sum_{i=1}^{n}h(i)=\sum_{d=1}^{n}g(d)\cdot S(\lfloor\frac{n}{d}\rfloor)
\]
\[\sum_{i=1}^{n}h(i)=g(1)\cdot S(n)+\sum_{d=2}^{n}g(d)\cdot S(\lfloor\frac{n}{d}\rfloor)
\]
\[\to g(1)S(n)=\sum_{i=1}^{n}h(i)-\sum_{d=2}^{n}g(d)\cdot S(\lfloor\frac{n}{d}\rfloor)
\]
四、 Min25
思想:
\[\sum_{i=1}^nf(i) = \sum_{i \in Prime}f(i) + \sum_{i \notin Prime}f(i)
\]
分为两个部分,第一部分是所有素数,第二部分是所有的合数
第一部分
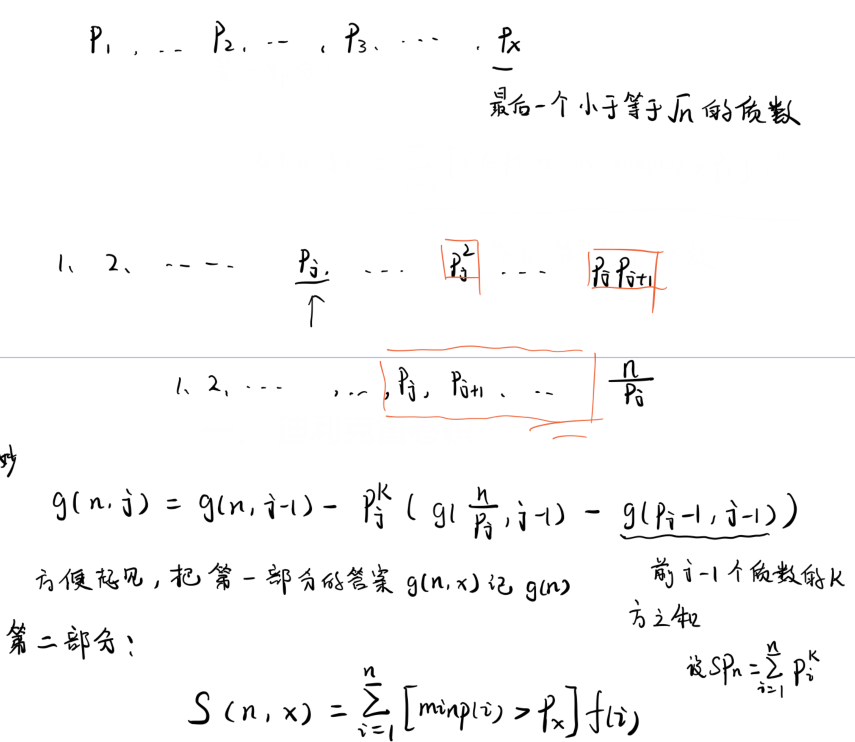
搞来一个这样的函数 \(g(n,j)\)
\[g(n,j) = \sum_{i=1}^n[i \in Prime\ or\ minp(i) > P_j] i^k
\]
所有的素数加上满足\(minp(i) > P_j\) 的所有 \(i\)
\([1-n]\) 中所有质数的 \(k\) 次方之和就是 \(g(n,x)\) ,\(P_x\) 是最后一个小于等于
\(\sqrt n\) 的质数
考虑 \(g(n,j)\) 的转移
\[g(n,j) = g(n,j-1) - P_j^k\bigg(g(\dfrac n {P_j},j-1)\ -g(P_j-1,j-1)\bigg)
\]
这个东西自己在纸上写一些体会一下,注意 \(P_j\) 筛去的第一个数是 \(P_j^2\) , 第二个数不是 \(P_j^2+ P_j\)
第二部分
设
\[S(n,x) = \sum_{i=1}^n[minp(i) > P_x]f(i)
\]
可以把 \(S(n,x)\) 也分成两部分,一部分是所有大于 \(P_x\) 的质数,另一部分是最小质因数大于 \(P_x\) 的合数,枚举最小质因子
\[S(n,x) = g(n) - sp_x + \sum_{p_k^e \le n \&k>n}f(p_k^e)\bigg(S \bigg(\dfrac n {p_k^e}\bigg) + [e \ne 1]\bigg)
\]
当 \(e = 1\) 的时候, \(P_k\) 在前面枚举过了,不等于 \(1\) 时,需要加上 \(P_k^e\)
存下所有可能的 \(\lfloor\dfrac n x \rfloor\) , 做一个映射
\[idx(x)= \begin{cases}ind1[x] , \ \ x\le \sqrt n \\ind2[n/x],\ \ x>\sqrt n\end{cases}
\]

