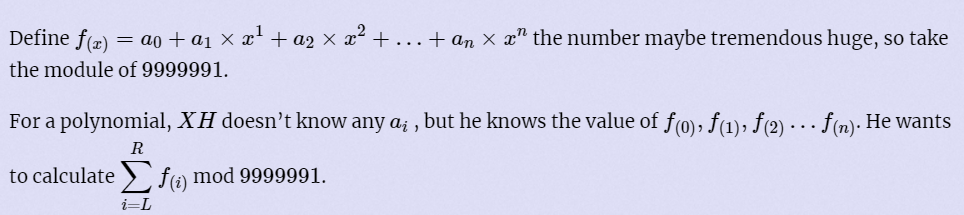拉格朗日插值法

\(n\) 阶的多项式 \(f(x)\) 可以由 \(n+1\) 个点确认。

若现有 \(n+1\) 个点 \((x_i,y_i) \ \ , \ i \in [0,n]\) 在 \(f(x)\) 上

则可以计算任意值 \(k\) 的函数值 \(f(k)\)

\[f(k) = \sum_{i=0}^ny_i\prod_{j\ne i}\dfrac {k-x_j} {x_i - x_j} \]

例如二次函数 \(f(x)\) 经过了 \((1,4) , (2,9) , (3,16)\) 三个点，则带入公式中

\[f(k) = 4\dfrac {(k-2)(k-3)}{(1-2)(1-3)} + 9\dfrac{(k-1)(k-3)}{(2-1)(2-3)} + 16 \dfrac {(k-1)(k-2)}{(3-1)(3-2)} \]

不难看出，当 \(k = x_i\) 的时候， \(f(k) = y_i\) ,且\(f(k)\) 是二次函数。

所以正确性可以保证

这样计算的时间复杂度是 \(O(n^2)\)

特殊情况

若 \(x_i = i\) ， 即 \(n\) 阶多项式 \(f(x)\) 在 \(0,1,2,...,n - 1\) 处的函数值

则

\[f(k) = \sum_{i=0}^ny_i\prod_{j\ne i}\dfrac {k-j} {i - j} \]

我们考虑 \(\prod_{j\ne i}\dfrac {k-j} {i - j}\) 的计算

对于某个 \(k\) ,我们可以预处理出 \(k - j\) 的前缀积和后缀积。分母是 \(i!(n-i)!(-1)^{n-i}\)

时间复杂度 \(O(n)\)

例题： 2019南昌邀请赛 B -Polynomial

先算出 \(f(n+1)\) ,然后就有了 \(S(1),...,S(n+1)\) 就可以用 \(S\) 插值计算 \(S(R) - S(L-1)\)

/*
 * @Author: zhl
 * @Date: 2020-11-12 14:50:58
 */
#include<bits/stdc++.h>
#define int long long
using namespace std;

const int mod = 9999991, N = 1e3 + 10;
int y[N], S[N];

int qpow(int a, int p) {
	int ans = 1;
	while (p) {
		if (p & 1)ans = (ans * a) % mod;
		a = (a * a) % mod;
		p >>= 1;
	}
	return ans;
}

int fac[N], invf[N];
void init() {
	fac[0] = invf[0] = 1;
	for (int i = 1; i < N; i++) {
		fac[i] = i * fac[i - 1] % mod;
	}
	invf[N - 1] = qpow(fac[N - 1], mod - 2);
	for (int i = N - 2; i >= 0; i--) {
		invf[i] = invf[i + 1] * (i + 1) % mod;
	}
}
int pre[N], suf[N];

int cal(int* a, int n, int k) {
	pre[0] = k; suf[n + 1] = 1;
	for (int i = 1; i <= n; i++)pre[i] = pre[i - 1] * (k - i) % mod;
	for (int i = n; i >= 0; i--)suf[i] = suf[i + 1] * (k - i) % mod;

	int ans = 0;
	for (int i = 0; i <= n; i++) {
		int f = invf[n - i] * invf[i] % mod;
		if ((n - i) & 1)f = -f;
		ans = (ans + a[i] * f % mod * (i == 0 ? 1 : pre[i - 1]) % mod * suf[i + 1]) % mod;
		if (ans < 0) ans += mod;
	}
	return ans;
}

int T, n, m;
signed main() {
	init();
	scanf("%lld", &T);
	while (T--) {
		scanf("%lld%lld", &n, &m);
		for (int i = 0; i <= n; i++) {
			scanf("%lld", y + i); if (i > 0) S[i] = (S[i - 1] + y[i]) % mod; else S[i] = y[i];
		}
		y[n + 1] = cal(y, n, n + 1);
		S[n + 1] = (S[n] + y[n + 1]) % mod;
		while (m--) {
			int l, r;
			scanf("%lld%lld", &l, &r);
			int ans = cal(S, n + 1, r) - cal(S, n + 1, l - 1);
			if (ans < 0)ans += mod;
			printf("%lld\n", ans % mod);
		}
	}
}
/*
1
3 2
1 10 49 142
6 7
95000 100000
*/