2019ICPC上海网络赛
D - Counting Sequences I
题意:
给 \(n\) , \(1 \le n \le 3000\)
问满足 \(\sum_{i=1}^na_i = \prod_{i=1}^na_i\)
的方案数,对 \(1e9+7\) 取模
思路:
可以暴力打表,用排列公式
\[\dfrac {N!} {a_1!a_2!...a_m!} \]加上发现的一些剪枝,可以在一分钟左右算出全部答案
#include<cstdio>
#include<iostream>
using namespace std;
const int mod = 1e9 + 7;
const int N = 3005;
typedef long long ll;
ll fac[N], inv[N];
int a[N], n;
ll ans;
ll qpow(ll a, ll b)
{
ll ans = 1;
while (b)
{
if (b & 1) ans = ans * a % mod;
a = a * a % mod;
b >>= 1;
}
return ans;
}
void dfs(int pos, int u, int add, int pro)
{
if (pos > n)
{
if (add == pro)
{
ll tmp = fac[n], cnt = 1;
for (int i = 2; i <= n; i++)
if (a[i] == a[i - 1]) cnt++;
else
{
tmp = tmp * inv[cnt] % mod;
cnt = 1;
}
tmp = tmp * inv[cnt] % mod;
ans = (ans + tmp) % mod;
}
return;
}
if (pro > 2*n) return;
if (u == 1 and (n - pos + 1) + add != pro) return;
if ((n - pos + 1) + add < pro) return;
for (int i = u; i >= 1; i--)
{
a[pos] = i;
dfs(pos + 1, i, add + i, pro * i);
//a[pos] = 0;
}
}
int main()
{
//freopen("D:\\1.txt", "w", stdout);
fac[0] = 1;
for (int i = 1; i < N; i++)
fac[i] = fac[i - 1] * i % mod;
inv[N - 1] = qpow(fac[N - 1], mod - 2);//阶乘的逆元
for (int i = N - 2; i >= 0; i--)
inv[i] = inv[i + 1] * (i + 1) % mod;
putchar('{');
for (n = 2; n <= 3000; n++)
{
ans = 0;
dfs(1, n, 0, 1);
printf("%lld", ans);
if (n != 3000)
putchar(',');
else
putchar('}');
}
return 0;
}
F - Rhyme scheme
题目大意:
用字符表示集合的划分
给定 \(n\) 问第 \(k\) 小的划分
思路:
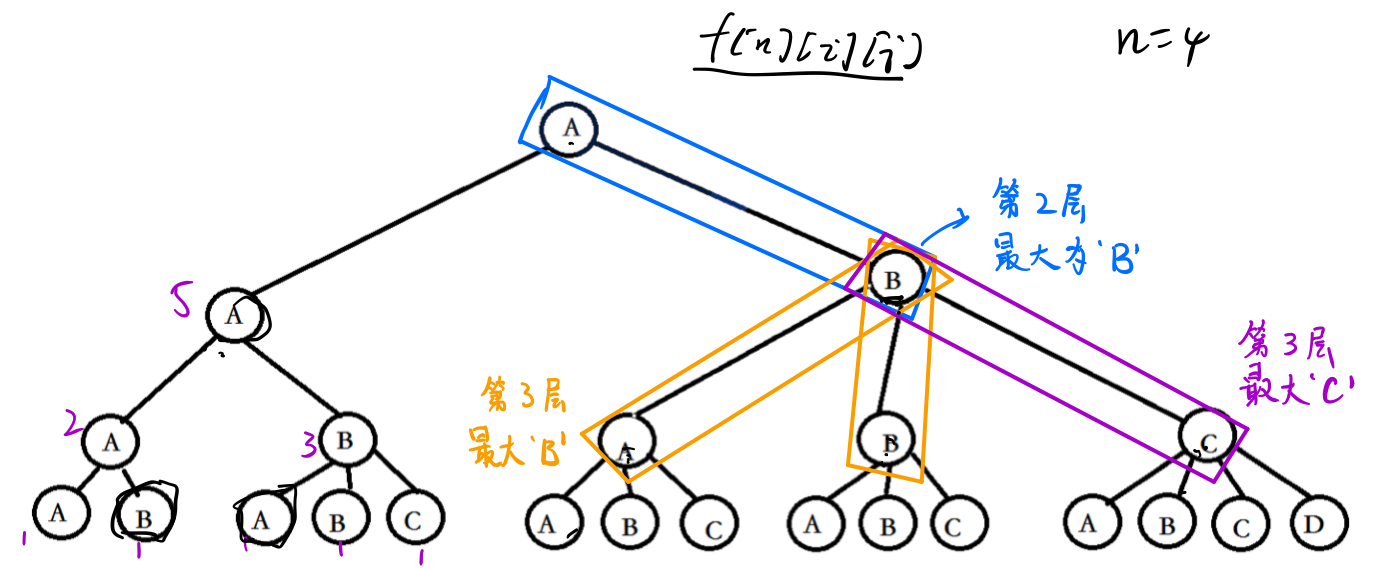
如图,所有的叶子节点从左到右就是 $n = 4 $ 的时候的所有集合划分
设状态表示 \(f[n][i][j]\) 表示的是总层数 \(n\) , 目前层数 \(i\) ,且由根节点到它的路径上最大的字母为 \(j\) 的点的集合 ,集合的属性是该节点下叶子节点的数目
显然当 \(i == n\) 时,\(f[n][i][j]=1\) ,即到了最后一层,都是叶子节点。
否则如上图蓝色标注的 \(B\) 节点,若 最大字母不变则有 \(j\) 棵相同的子树,否则加上一颗增加了的子树。
\(f[n][i][j] = f[n][i+1][j]*j + f[n][i+1][j+1]\)
然后就可以直接用这些信息去找答案了,类似找 \(k\) 大这样。
需要注意 \(B_{26}\) 爆了 $long\ long $
#include<bits/stdc++.h>
using namespace std;
int T, n;
__int128 k;
__int128 f[30][30][30];
void read(__int128& x) {
x = 0;
int f = 1;
char ch = getchar();
while (!(ch >= '0' && ch <= '9')) ch = getchar();
x = x * 10 + ch - '0';
while ((ch = getchar()) >= '0' && ch <= '9')
x = x * 10 + ch - '0';
x *= f;
}
void init() {
for (int n = 1; n <= 26; n++)
for (int i = n; i >= 1; i--)
if (i == n) {
for (int j = 1; j <= i; j++) f[n][i][j] = 1ll;
}
else {
for (int j = 1; j <= i; j++) f[n][i][j] = f[n][i + 1][j] * j + f[n][i + 1][j + 1];
}
}
int main() {
init();
scanf("%d", &T); int c = 0;
while (T--) {
scanf("%d", &n);
read(k);
printf("Case #%d: ", ++c);
int now = 0, j;
for (int i = 1; i <= n; i++) {
for (j = 1; j <= now; j++) {
if (k <= f[n][i][now]){
break;
}
k -= f[n][i][now];
}
putchar('A' + j - 1);
now = max(now, j);
}
puts("");
}
}
C - Triple
题意
给三个数组 \(A,B,C\) 问有多少个 \((i,j,k)\) 使得
\(A_i,B_j,C_k\) 中较小的两个数的和大于等于最大的数
\(1 \le T \le 100\)
\(1 \le A_i,B_i,C_i,n \le 100,000\)
There are at most \(20\) test cases with \(N>1000\)
思路
用容斥思想,所有不和法的方案就是 较小的两数相加小于第三个数的方案。
处理出 所有的 \(A_i + B_j\) ,然后对于每一个 \(C_k\) ,只要加上所有小于 \(C_k\) 的方案数就可以
这里小数据用暴力,大数据用 多项式乘法
/*
* @Author: zhl
* @Date: 2020-11-09 15:23:52
*/
#include<bits/stdc++.h>
#define rep(i,a,b) for(int i = a;i <= b;i++)
#define mem(a,b) memset((a),(b),sizeof(a))
using namespace std;
typedef long long ll;
const double pi = acos(-1.0);
const int N = 6e5 + 10;
struct cp {
double x, y;
cp() {}
cp(double _x, double _y) {
x = _x; y = _y;
}
cp operator + (cp b) {
return cp(x + b.x, y + b.y);
}
cp operator -(cp b) {
return cp(x - b.x, y - b.y);
}
cp operator *(cp b) {
return cp(x * b.x - y * b.y, x * b.y + y * b.x);
}
};
int rev[N];
int bit = 0;
int lim;
void FFT(cp* a, int inv) {
for (int i = 0; i < lim; i++) {
if (i < rev[i]) {
swap(a[i], a[rev[i]]);
}
}
for (int mid = 1; mid < lim; mid <<= 1) {
cp temp(cos(pi / mid), inv * sin(pi / mid));
for (int i = 0; i < lim; i += mid * 2) {
cp omega(1, 0);
for (int j = 0; j < mid; j++, omega = omega * temp) {
cp x = a[i + j], y = omega * a[i + j + mid];
a[i + j] = x + y, a[i + j + mid] = x - y;
}
}
}
}
int T, n, A[N], B[N], C[N], tA[N], tB[N], tC[N];
cp x[N], y[N];
ll sum[N];
ll solve_small(int* a, int* b, int* c) {
for (int i = 0; i <= c[n - 1]; i++)sum[i] = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
sum[a[i] + b[j]]++;
}
}
ll ans = 0;
for (int i = 1; i <= c[n - 1]; i++)sum[i] += sum[i - 1];
for (int i = 0; i < n; i++) ans += sum[c[i] - 1];
return ans;
}
ll solve_big(int* a, int* b, int* c) {
for (int i = 0; i <= lim; i++)x[i] = cp(a[i], 0), y[i] = cp(b[i], 0);
FFT(x, 1); FFT(y, 1);
for (int i = 0; i <= lim; i++)x[i] = x[i] * y[i];
FFT(x, -1);
mem(sum, 0);
ll ans = 0;
for (int i = 0; i <= c[n - 1]; i++)sum[i] = signed(x[i].x / lim + 0.5);
for (int i = 1; i <= c[n - 1]; i++)sum[i] += sum[i - 1];
for (int i = 0; i < n; i++) ans += sum[c[i] - 1];
return ans;
}
int main() {
scanf("%d", &T); int c = 0;
while (T--) {
scanf("%d", &n);
mem(tA, 0); mem(tB, 0); mem(tC, 0);
lim = 1; bit = 0;
while (lim <= (2 * n))lim <<= 1, bit++;
mem(rev, 0);
for (int i = 0; i < lim; i++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
for (int i = 0; i < n; i++)scanf("%d", A + i), tA[A[i]]++; sort(A, A + n);
for (int i = 0; i < n; i++)scanf("%d", B + i), tB[B[i]]++; sort(B, B + n);
for (int i = 0; i < n; i++)scanf("%d", C + i), tC[C[i]]++; sort(C, C + n);
printf("Case #%d: ", ++c);
if (n <= 1000) {
printf("%lld\n", 1ll * n * n * n - solve_small(A, B, C) - solve_small(A, C, B) - solve_small(B, C, A));
}
else {
printf("%lld\n", 1ll * n * n * n - solve_big(tA, tB, C) - solve_big(tA, tC, B) - solve_big(tB, tC, A));;
}
}
}