Ac自动机 & 矩阵
其实不算很难的一个算法
先建一个 Tire树 ,然后bfs构造 fail 指针
\(Fail\) 的含义
若一个节点 \(i\) 的 \(fail[i] = j\) ,则表示从 \(root\) 到 \(j\) 的字符串是 \(root\) 到 \(i\) 的字符串的一个后缀
#include<bits/stdc++.h>
using namespace std;
const int N = 6e6 + 10;
queue<int>q;
struct {
int c[N][26], fail[N], val[N], cnt;
void insert(char* s) {
int len = strlen(s); int now = 0;
for (int i = 0; i < len; i++) {
int v = s[i] - 'a';
if (!c[now][v])c[now][v] = ++cnt;
now = c[now][v];
}
val[now]++;
}
void getFail() {
for (int i = 0; i < 26; i++) {
if (c[0][i])fail[c[0][i]] = 0, q.push(c[0][i]);
}
while (!q.empty()) {
int u = q.front(); q.pop();
for (int i = 0; i < 26; i++) {
if (c[u][i]) {
fail[c[u][i]] = c[fail[u]][i];
q.push(c[u][i]);
}
else c[u][i] = c[fail[u]][i];
}
}
}
int query(char* s) {
int len = strlen(s); int now = 0, ans = 0;
for (int i = 0; i < len; i++) {
now = c[now][s[i] - 'a'];
for (int t = now; t && val[t] != -1; t = fail[t]) {
ans += val[t];
val[t] = -1;
}
}
return ans;
}
}Ac;
int n;
char p[N];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%s", p);
Ac.insert(p);
}
Ac.getFail();
scanf("%s", p);
printf("%d\n", Ac.query(p));
}
Ac自动机 + 矩阵快速幂
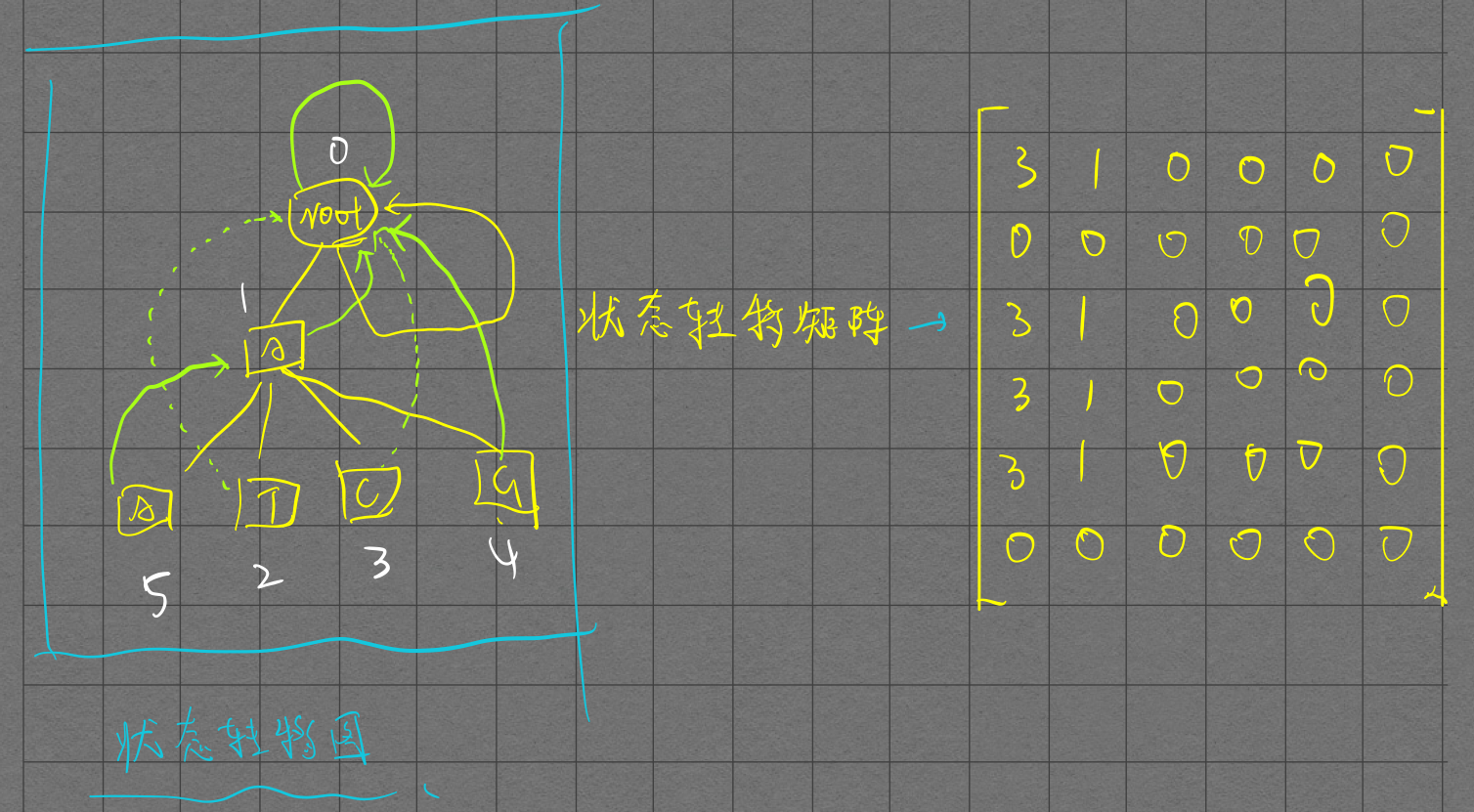
其实Ac自动机的Tire树就是一个状态转移图,构造出状态转移矩阵, \(M_{ij}\) 表示从Tire树上的第 \(i\) 个节点转移到 \(j\) 节点的方案数, \(M^n\) 就是长度为 \(n\) 的串的状态转移矩阵, \(M_{0i}\) 表示从根节点转移到 \(i\) 经过 \(n\) 次的方案数,\(ans= \sum_iM_{0i}\)
在处理Tire树的时候要稍微注意一些小的细节。
主要就是标记的传递
if(val[fail[u]]) val[u] = 1
以输入:
4 3 AT AC AG AA为例
#include<cstdio>
#include<map>
#include<cstring>
#include<queue>
#include<string>
#define int long long
using namespace std;
const int N = 5e5 + 10;
queue<int>q;
const int mod = 1e5;
map<char, int>id;
struct Mat {
int m[100][100], n;
Mat(int _n, int v) {
n = _n;
memset(m, 0, sizeof m);
for (int i = 0; i < n; i++)m[i][i] = v;
}
Mat operator *(const Mat& b)const {
Mat res = Mat(b.n, 0);
int n = b.n;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) {
res.m[i][j] = (res.m[i][j] + m[i][k] * b.m[k][j]) % mod;
}
}
}
return res;
}
};
struct {
int c[N][4], fail[N], val[N], cnt;
void insert(char* s) {
int len = strlen(s); int now = 0;
for (int i = 0; i < len; i++) {
int v = id[s[i]];
if (!c[now][v])c[now][v] = ++cnt;
now = c[now][v];
}
val[now]++;//这里写++好像过不去
//val[now] = 1;
}
void clear() {
memset(c, 0, sizeof c);
memset(val, 0, sizeof val);
cnt = 0;
memset(fail, 0, sizeof fail);
}
void getFail() {
for (int i = 0; i < 4; i++) {
if (c[0][i])fail[c[0][i]] = 0, q.push(c[0][i]);
}
while (!q.empty()) {
int u = q.front(); q.pop();
//***
if (val[fail[u]] == 1) {
val[u] = 1;
}
for (int i = 0; i < 4; i++) {
if (c[u][i]) {
fail[c[u][i]] = c[fail[u]][i];
q.push(c[u][i]);
}
else c[u][i] = c[fail[u]][i];
}
}
}
int query(char* s) {
int len = strlen(s); int now = 0, ans = 0;
for (int i = 0; i < len; i++) {
now = c[now][id[s[i]]];
for (int t = now; t && val[t] != -1; t = fail[t]) {
ans += val[t];
val[t] = -1;
}
}
return ans;
}
Mat getMat() {
//这里是cnt + 1
Mat res = Mat(cnt+1, 0);
for (int i = 0; i <= cnt; i++) {
for (int j = 0; j < 4; j++) {
if (!val[c[i][j]]) {
res.m[i][c[i][j]]++;
}
}
}
return res;
}
}Ac;
Mat qpow(Mat a, int p) {
Mat res = Mat(a.n, 1);
while (p) {
if (p & 1) res = a * res;
a = a * a;
p >>= 1;
}
return res;
}
int n;
char p[N];
signed main() {
char s[] = "ACGT";
for (int i = 0; i < 4; i++)id[s[i]] = i;
int n, m, x;
while (~scanf("%lld%lld", &m, &n)) {
Ac.clear();
for (int i = 0; i < m; i++) {
scanf("%s", p);
Ac.insert(p);
}
Ac.getFail();
Mat mat = Ac.getMat();
mat = qpow(mat, n);
int ans = 0;
for (int i = 0; i < mat.n; i++) {
ans = (ans + mat.m[0][i]) % mod;
}
printf("%lld\n", ans);
}
}
其实就是一个模板题
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 7e5 + 10;
queue<int>q;
const int mod = 1e9 + 7;
struct Mat {
int m[500][500], n;
Mat(int _n,int v) {
n = _n;
memset(m, 0, sizeof m);
for (int i = 0; i < n; i++)m[i][i] = v;
}
Mat operator *(const Mat& b)const {
Mat res = Mat(b.n,0);
int n = b.n;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) {
res.m[i][j] = (res.m[i][j] + m[i][k] * b.m[k][j]) % mod;
}
}
}
return res;
}
};
struct {
int c[N][26], fail[N], val[N], cnt;
void insert(char* s) {
int len = strlen(s); int now = 0;
for (int i = 0; i < len; i++) {
int v = s[i] - 'a';
if (!c[now][v])c[now][v] = ++cnt;
now = c[now][v];
}
//val[now]++;
val[now] = 1;
}
void getFail() {
for (int i = 0; i < 26; i++) {
if (c[0][i])fail[c[0][i]] = 0, q.push(c[0][i]);
//***
else c[0][i] = 0;
}
while (!q.empty()) {
int u = q.front(); q.pop();
//***
if (val[fail[u]] == 1) {
val[u] = 1;
}
for (int i = 0; i < 26; i++) {
if (c[u][i]) {
fail[c[u][i]] = c[fail[u]][i];
q.push(c[u][i]);
}
else c[u][i] = c[fail[u]][i];
}
}
}
int query(char* s) {
int len = strlen(s); int now = 0, ans = 0;
for (int i = 0; i < len; i++) {
now = c[now][s[i] - 'a'];
for (int t = now; t && val[t] != -1; t = fail[t]) {
ans += val[t];
val[t] = -1;
}
}
return ans;
}
Mat getMat() {
//这里 cnt 也能过,但是上面的POJ会wa,这里数据的问题,应该是cnt+1
Mat res = Mat(cnt + 1, 0);
for (int i = 0; i <= cnt; i++) {
for (int j = 0; j < 26; j++) {
if (!val[c[i][j]]) {
res.m[i][c[i][j]]++;
}
}
}
return res;
}
}Ac;
Mat qpow(Mat a, int p) {
Mat res = Mat(a.n, 1);
while (p) {
if (p & 1) res = a * res;
a = a * a;
p >>= 1;
}
return res;
}
int n;
char p[N];
signed main() {
int n, m, x;
scanf("%lld%lld", &n, &m);
for (int i = 0; i < m; i++) {
scanf("%lld%s", &x, p);
Ac.insert(p);
}
Ac.getFail();
Mat mat = Ac.getMat();
mat = qpow(mat, n);
int ans = 0;
for (int i = 0; i < mat.n; i++) {
ans = (ans + mat.m[0][i]) % mod;
}
printf("%lld\n", ans);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号