走过路过不要错过 包你一文看懂支撑向量机SVM

假设我们要判断一个人是否得癌症,比如下图：红色得癌症,蓝色不得.

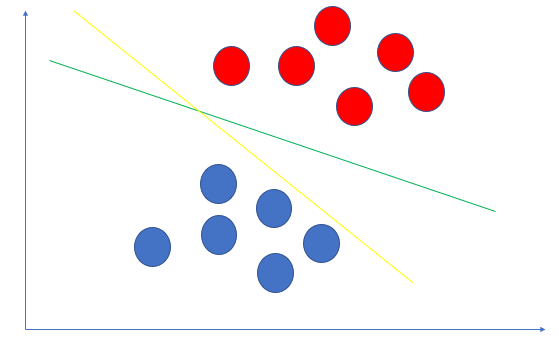
看一下上图,要把红色的点和蓝色的点分开,可以画出无数条直线.上图里黄色的分割更好还是绿色的分割更好呢？直觉上一看,就是绿色的线更好.对吧.

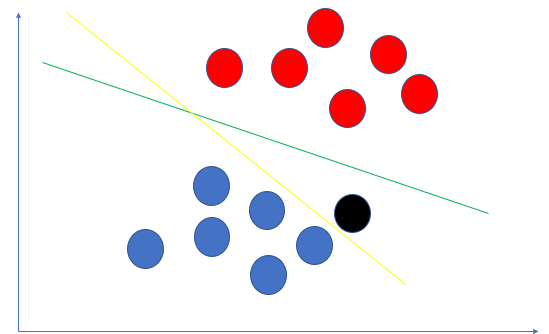
为啥呢？考虑下图,新来了一个黑色点,明显靠蓝色点更近,如果用黄线分割,却把它划分到了红色点这个类别里.

 现在细想一下为什么绿线比黄线分隔效果更好？

  • 黄色线太贴近蓝色点
  • 绿色线到红色点群和蓝色点群距离大致相等.恰好位于两个点群中间的位置

 

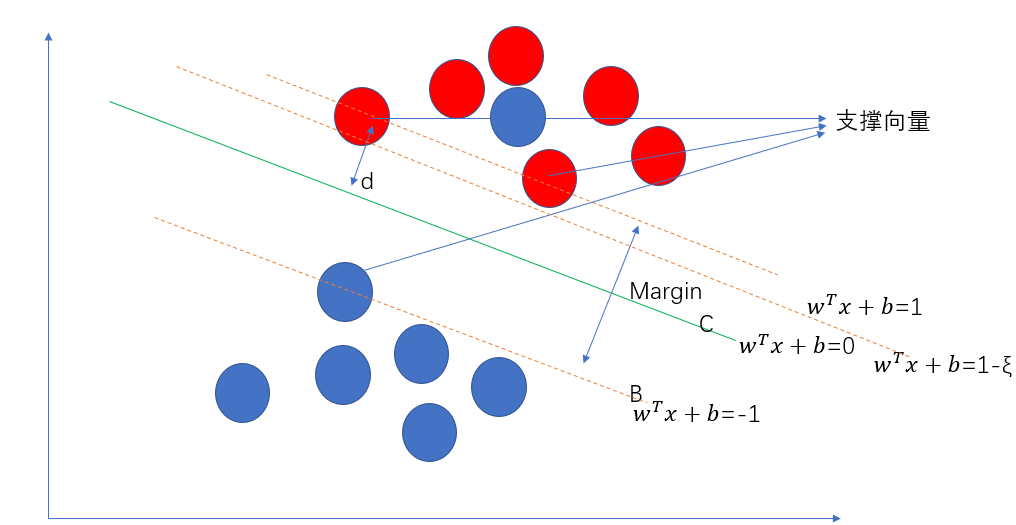
由此我们就引申出了SVM的理论基础：使得距离决策边界最近的点的距离之和最远.  我屮艸芔茻,纳尼？？这都是啥. 别慌,看下图：

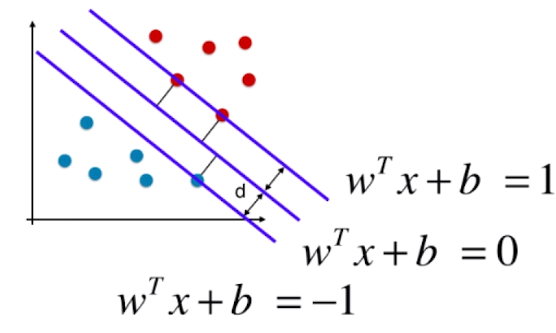
还是上面的问题,什么样的分隔线才是最好的？答案是上图中的绿色线条C.  

  1. 线条A平行于C平行于B.  
  2. d代表距离C最近的点到C的距离.
  3. margin代表A到B的距离,margin=2d.

我们想寻找的最优分割线其实就是使得margin最大,margin最大意味着红色点和蓝色点被尽可能的分开了.  同时这个分隔线又得不偏不倚,既不偏向红点,也不偏向蓝点,

所以C是A，B正中间的线.

也就是说,A穿过的两个红点和B穿过的蓝点决定了C的位置.我们把其称为支撑向量.  这也是SVM叫做支撑向量机算法的由来.

 

Hard Margin SVM

假设数据是线性可分的,则我们找得到一条线将数据一分为二.这种情况下我们称之为hard margin svm。

上图中的C在二维空间(即平面)中是一条线. 推广到N维空间中,是一个N-1维的超平面.我们把这个超平面定义为$w^Tx + b = 0$。则任意一点到该超平面的距离为$\frac {|w^Tx+b|} {||w||^2}$

(用二维平面上点(x,y)到直线ax+by+c=0的距离去思考一下,高维空间就别想象了,毕竟人类这种生物是无法理解超过三维空间的)

超平面上方,红球的label我们定义为y=1,超平面下方,蓝色球的label定义为y=-1.(和逻辑回归一样,SVM本身只能解决二分类问题,当然我们可以通过不断SVM的方式以达到解决多分类的问题,这里略去不表.) 则对任意球,到这个超平面距离都大于d。

在分隔平面上方,$w^Tx^i + b$ > 0,y=1,在分隔平面下方，$w^Tx^i + b$ < 0,y=-1。所以我们有

$$y^i \frac{w^Tx^i + b} {||w||^2} \ge d$$,可以转换为 $$y^i \frac{w^Tx^i + b} {d||w||^2} \ge 1$$. $d||w||^2$是一个标量,所以可以改写成

$$y^i(w_d^Tx^i + b_d)\ge 1$$为了表示的方便,记为$$y^i(w^Tx^i + b) \ge 1$$

所以可得下图所示：

 对于任意的支撑向量$x^i$而言,$d=\frac {|w^Tx^i + b|} {||w||^2} = \frac 1{||w||^2}$。我们的目标是最大化margin，也就是最大化d，也就是最小化$||w||$。实际中,为了求导的方便,通常转换为最小化$\frac 1 2 ||w||^2$

从而我们的svm的求解转换为一个限定条件下的最优化问题.

$$ \left\{\begin{aligned}  {min \frac 1 2 ||w||^2 \\  S.T. \ \ \ y^{(i)}(w^T x^{(i)} + d) \ge 1}   \end{aligned}\right.$$

限定条件下的最优化问题要比全局最优化问题背后的数学推导复杂太多了,不在本篇说明了。以上,我们基本理解了svm的原理.

 

Soft Margin SVM

上面,我们假设数据是线性可分的,即我们找得到直线C分割成2部分.但这种假设太理想了,更多的情况下,我们找不到一条直线分隔出红蓝球.如下图：

 

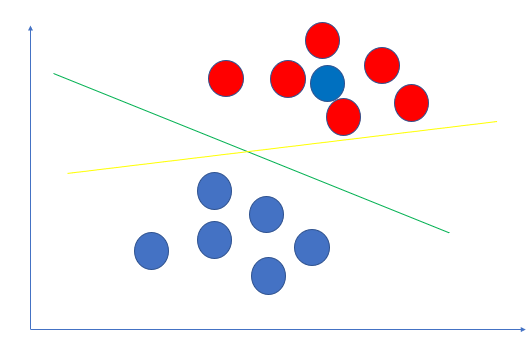
别管红色点中的那个扎眼的蓝色点到底是一个错误的样本还是一个特殊的样本,总之吧,这种情况下,是找不出一条直线分隔出两种点的.也就是线性不可分.

回顾一下上文的约束条件：$$S.T. \\y^i(w^T x^i + d) \ge 1$$，这意味着分隔出来的区域最大.

  • 红色的点在分隔线的上方,y=1,到分隔线的距离>d。
  • 蓝色的点在分隔线的下方,y=-1,到分隔线的距离>d。

现在为了让我们的分隔线有一定的容错性,我们把它改成

$$ S.T. \ \ y^{(i)}(w^T x^{(i)} + d) \ge 1-\zeta_i   \\ \zeta_i \ge 0$$

注意：

  • 这里的$\zeta_i$不是一个常量,对每一个样本点,都有一个$\zeta_i$,即我们的模型对每一个样本都有容错能力.
  • $\zeta_i  \ge 0$，假如<0的话,相当于将A这条线上移.本来满足条件的红色点都变得不满足了.违背了我们的本意：放宽我们的限定条件.

但是我们的系统作为一个整体,不能容忍太多的错误.所以我们的目标优化函数调整为

$$ min \frac 1 2 ||w||^2 + \sum_{i=1}^{m}\zeta_i$$

此时$min \frac 1 2 ||w||^2$ 和$\sum_{i=1}^{m}\zeta_i$的比例是1:1,意味着我们对"寻找完美分隔超平面"和"模型的错误容忍度"同样看重,为了调整这种比例,即调整最优化时侧重的方面,我们的目标优化函数调整为$ min \frac 1 2 ||w||^2 + C\sum_{i=1}^{m}\zeta_i$

从而我们的问题转换为限定条件下的最优化问题$$ \left\{\begin{aligned}  {min \frac 1 2 ||w||^2  + C\sum_{i=1}^{m}\zeta_i \\  S.T. \ \ \ y^{(i)}(w^T x^{(i)} + d) \ge 1-\zeta_i}   \\  \zeta_i>0 \end{aligned}\right.$$

C越大,代表容错空间越小.

 L1/L2正则

上面的$\sum_{i=1}^{m}\zeta_i$即称为L1正则.$\sum_{i=1}^{m}\zeta_i^2$称为L2正则. 

正则项的加入,是为了提高模型的包容能力,也就是泛化能力.上面我们举的例子是数据是线性不可分的.实际上即便是线性可分的

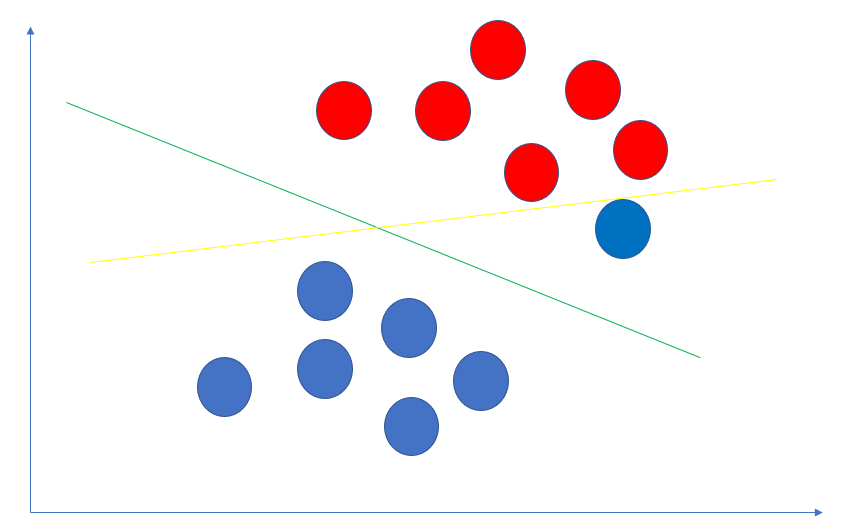
在真实的数据中,红色点群中的那个蓝色点很可能是一个误标记的样本. 如果按照hard margin svm的算法,会选择黄色的线作为分隔. 而实际上绿色的分隔线的模型效果更好,泛化能力更强.

 

多项式特征使用svm

soft margin svm中我们通过对放宽限定条件来解决样本不是线性可分的问题,但是,注意，此时我们的svm模型仍然是线性的.

在逻辑回归和多项式回归两篇博文中我们介绍了如何通过构造新特征,解决数据不存在线性关系的问题.同样的这一思路对svm也是有效的.

from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline

def PolynomialSVC(degree, C=1.0):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("linearSVC", LinearSVC(C=C))
    ])

poly_svc = PolynomialSVC(degree=3)
poly_svc.fit(X, y

 

核函数

上面的先构造多项式特征,再采用线性svm,可以理解为将特征从低维映射到高维,再做线性svm分隔.

 

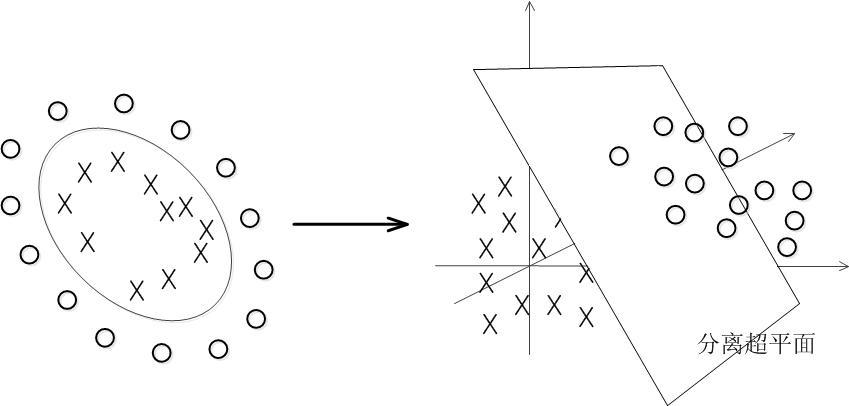
你可以借助这个例子来理解这个过程：你在桌面上(二维空间,平面)有2圈小球,这时候你是找不到直线分隔的,你使劲地砸一下桌子,让球全部飞起来,现在球就到了三维空间中,可以找到一个平面分隔将两类球分隔出来.

 

前面我们说过了svm实际上是一个限定条件下的最优化问题.

$$ \left\{\begin{aligned}  {min \frac 1 2 ||w||^2 \\  S.T. \ \ \ y^{(i)}(w^T x^{(i)} + d) \ge 1}   \end{aligned}\right.$$

实际上在求解的时候是转化成(不要问我怎么转换的,其中用到的数学推导我已经看不明白了.......)

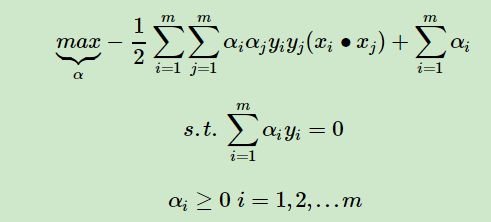
注意到其中的没有？  

试想,如果我们用上述的多项式转换,先把特征转成高维的,比如原有特征有2个,转换为200个,$x_i \dot x_j$将有多少种组合？转换为2000个,20000个呢？此时,为了存储更多的特征,需要用到更多的内存,这还不是最重要的,关键的是带来的计算量增长将是灾难性的.

这时候核函数就闪亮登场了：

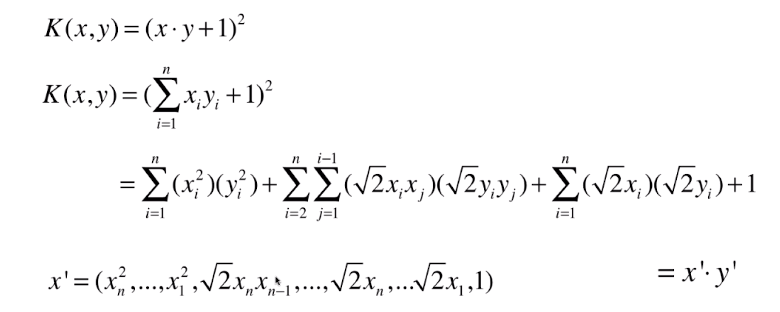
我们把上面公式里的x,y视为原始特征值,从$x \dot y$ ,经过K(x,y)后完成了$x \dot y$到$x' \dot y'$的转换,x'和y'是多项式转换后的新特征, x'和我们做二阶多项式转换后的特征是不是很像,区别只是有的特征前有个$\sqrt {2}$的系数,这个系数对我们模型训练无所谓,因为我们的模型是线性的,无非就是原先的系数矩阵的某一维度除以$\sqrt {2}$就是了.

所以我们可以把公式内的$x_i \dot x_j$用$K(x_i,x_j)$替代.实现低维度到高维度的特征转换后的效果.

注意：我们实现了特征低维度转高维度后再训练的效果,但是$K(x_i,x_j)$的计算仍然是在原有维度的！！！！

核函数就是这样一种trick,帮助我们做到在高维空间(甚至是无限维度空间)运算的trick。并没有真正的做低维到高维的特征转换.核函数也不是svm独有的技巧.事实上,核函数的研究比svm算法的出现早了几十年.

 

上面我们用二阶多项式的例子描述了核函数的原理.

常见的核函数有：

  • 多项式核 $\kappa(x, x_i) = ((x\cdot x_i) + 1)^d$
  • 线性核 $\kappa(x,x_i) = x \cdot x_i$
  • 高斯核 $\kappa(x, x_i) = exp(-\gamma {||x - x_i||^2})$
  • sigmoid核 $\kappa(x, x_i) = tanh(\eta<x, x_i> + \theta)$

高斯核函数

高斯核函数是比较常用的一个核函数,它可以把m*n（m为样本数量,n为样本特征维度）的数据映射成m*m维.当我们的数据的特征维度特别高,而样本数又不多时,就可以了使用这种方法,大大减少计算开销.比如自然语言处理中就常用.

$\kappa(x, x_i) = exp(-\gamma {||x - x_i||^2})$,以2*10的数据为例（2个样本,每个样本10个特征）

x转变为$(\exp(-\gamma {||x - x_1||^2})，\exp(-\gamma {||x - x_2||^2}))$ .即我们以每一个数据点作为参考点（地标点landmark）,加以转换,从而将数据转换为m维.

对比一下高斯分布的函数$f(x) = \frac 1 {\sigma \sqrt {2 \pi}} e^{-\frac {(x-\mu)^2} {2\sigma^2}}$ 。你可以把$\gamma$理解为$-\frac 1 {2\sigma^2}$.学过概率论的话就知道高斯分布图如下：

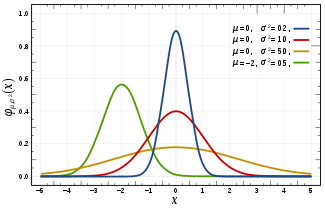
由此,我们知道$\gamma$越大(即$\sigma$越小),分布越集中. 反映到模型中即单个样本的影响越大,最终绘制出的决策边界会围绕着样本点,容易过拟合.如下分别为$\gamma=100$和$\gamma=10$时对同样的数据用svm训练得到的模型的决策边界.

 

 

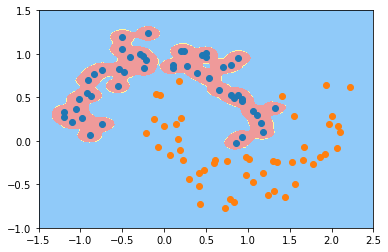
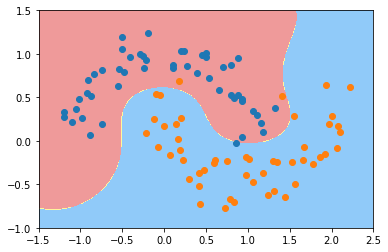
使用svm需要注意的一些事项：

对数据进行标准化，和knn一样,因为涉及到了距离的计算. 不同特征的量纲的不同会带来很大影响.

C越大,对错误分类的容忍性越小.

$\gamma$越大,即标准差越小,决策边界越容易围绕样本,容易过拟合.

 

SVM思想解决回归问题

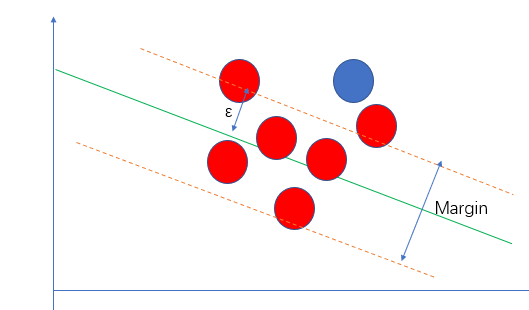
前面讲svm分类原理的时候,提到要使margin区域尽可能大,也就是区域内的点尽可能少,相应的,解决回归问题即要使得margin区域内的点越多越好.

Margin边界到拟合直线的距离称为$\epsilon$是SVM解决回归问题的一个超参数。

sklearn中相应的类是sklearn.svm包中的SVR.

posted @ 2019-01-23 09:18  core!  阅读(727)  评论(0)  编辑  收藏  举报