特征脸是怎么提取的之主成分分析法PCA
机器学习笔记 多项式回归这一篇中,我们讲到了如何构造新的特征,相当于对样本数据进行升维.
那么相应的,我们肯定有数据的降维.那么现在思考两个问题
- 为什么需要降维
- 为什么可以降维
第一个问题很好理解,假设我们用KNN训练一些样本数据,相比于有1W个特征的样本,肯定是训练有1K个特征的样本速度更快,因为计算量更小嘛.
第二个问题,为什么可以降维.一个样本原先有1W个特征,现在减少到1K个,不管如何变换,数据包含的信息肯定是减少了,这是毫无疑问的.但是信息的减少是否意味着我们对于样本的认知能力的下降?这个则未必.

以minist数据集为例,每一个数字图片都由N个像素构成,即样本有N个特征,但是我们不需要精确地知道每一个像素的值,依然能够分辨出这个数字是几,你可以通俗地理解为,比如你把每张图的边边角角都减掉,并不影响你识别这是几。 由此,我们知道,样本特征的重要性并不是一致的,有的重要,也即所谓的主成分.
现在问题则转换为:我们怎么样寻找到一种方法,使得降维后"重要的特征"尽可能地保留,也即降维后信息的丢失最少?
依然从一个极端的例子入手,假设我们有M个样本,每个样本2个特征,特征1的波动幅度很大,特征2的波动幅度很小.

此时,如果要把这M个样本降成1维,采用最简单粗暴的方式,丢弃一个特征,是丢弃feature1呢还是feature2呢?
如果,丢弃feature1的话,我们的样本就只剩下了feature2,而feature2的值在3附近微小的波动,几乎没有变化. 没有变化,机器学习算法就没法从中学习到足够的信息.比如M个样本对应着M个label,这M个label各不相同.来了个新样本,特征值还是3,这时候我们是没法推算出新样本的label的.
对机器学习算法而言,我们希望在合理的范围内,数据的分布越分散越好,即数据的方差越大越好,这样才能学习到足够多的信息.
而这也正是PCA降维的理论基础:我们希望找到一个新的N维坐标系,使得数据在这个新的N维坐标系的前K个坐标轴上分布,方差最大.这样的N维坐标系中的K个坐标轴就是我们所要寻找的K个主成分.
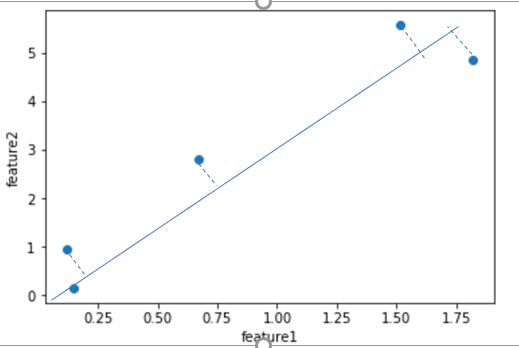
比如对这个图中的蓝色的点而言,我们希望找到一个向量w(图中的蓝色线),使得各点在w上的投影点,方差最大.样本点$X^{(i)}$投影到单位向量w后得到$X_p^{(i)}$,这些新的样本点的方差为$\frac{\sum_{i=1}^m (X_p^{(i)} - \overline X_p)^2)} m$,为了方便计算,在向w投影之前,我们对样本X做demean去均值处理,即每个特征值减去该维度特征的均值,这个操作并不会影响数据的分布.demean后的样本点投影到w后得到的新样本点的方差变为$\frac{\sum_{i=1}^m (X_p^{(i)})^2)} m$.注意这里$X_p^{(i)}$是一个向量.所以我们的方差可以转变为$$Var(X_p) = \frac{\sum_{i=1}^m || X_p^{(i)} ||^2)} m$$

注意,样本点$X^{(i)}$投影到单位向量w后得到$X_p^{(i)}$,由向量点乘的定义我们能够得到$X^{(i)} \cdot w = || X^{(i)}|| \cdot || w|| \cdot \cos \theta = || X^{(i)}|| \cdot \cos \theta = || X_p^{(i)} ||$.由此我们的目标转变为使得$$Var(X_p) = \frac{\sum_{i=1}^m X^{(i)} \cdot w^2)} m$$最大化.
接下来我们用梯度上升法求出这个w。现在先不用管梯度上升法是怎么回事,本篇重点在于理解PCA。梯度下降法梯度上升法以后会再写博文解释.这个w也就是我们的第一主成分.即样本投影到这个方向后,方差最大,损失信息最少.那么现在我们如何求出第二主成分呢?
求出这个w之后,注意w是一个N维向量. 我们就可以得到X在w之外剩余的分量为$X^{’(i)}=X^{(i)}-X_p^{(i)}=X^{(i)}-X^{(i) \cdot w}$,对$X^{’(i)}$,我们再次求出一个w2,使得其在w2上的投影的方差最大,求解方法同上.
我们不断循环这个过程,就可以求解出k个w,记做
$$W_k=\begin{bmatrix} W_1^{(1)}& W_2^{(1)}& … &W_n^{(1)} \\ W_1^{(2)}& W_2^{(2)}& … &W_n^{(2)} \\ … \\ W_1^{(k)}& W_2^{(k)}& … &W_n^{(k)} \\ \end{bmatrix}$$.即$$W_k=\begin{bmatrix} w_1\\ w_2 \\ … \\w_k\\ \end{bmatrix}$$
这个$W_k$即我们求出的新的N维坐标系的前K个坐标轴.
原始数据点在新的N维坐标系的第k个坐标轴的投影距离为$X^{(i)} \cdot w_k$,则原始样本在新的N维坐标系的前K个坐标轴上可以表示为$$X^{‘}=XW_k^T$$。这样我们就把矩阵M*N的矩阵X转换成了M*K的矩阵$X^{'}$,从而达到了降维的目的.
原理部分说完了,我们来看一下sklearn中的具体api使用.
class
sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False, svd_solver=’auto’, tol=0.0, iterated_power=’auto’, random_state=None)[source]¶
常用参数有n_components,代表降维后需要保留的维度数.如果0<n_components<1的话,表示降维后需要保留的方差比例.(你可以通俗地理解为保留的信息占原始信息的百分比)
常用属性:
explained_variance_ : array, shape (n_components,) 解释了新的坐标系中的k个坐标轴的每一个轴所解释的方差.
explained_variance_ratio_ : array, shape (n_components,) 解释了新的坐标系中的k个坐标轴的每一个轴所解释的方差所占百分比.
n_components_:主成分个数.即降到的维度数.
components_ : array, shape (n_components, n_features) 主成分.
这样说显得有点抽象,看个例子你就全明白.
from sklearn.decomposition import PCA pca = PCA(n_components=2) pca.fit(X_train) X_train_reduction = pca.transform(X_train) X_test_reduction = pca.transform(X_test) knn_clf = KNeighborsClassifier() knn_clf.fit(X_train_reduction, y_train)
我们把64维的X_train降成二维的X_train_reduction.
pca.explained_variance_
array([ 175.77007821, 165.73864334])
pca.explained_variance_ratio_
array([ 0.14566817, 0.13735469])
什么意思呢?降维后的X_train_reduction在第一个维度上(第一主成分)的方差为175.77,占比为14.56%.
来看下当我们将n_components传参为原始特征数量时
from sklearn.decomposition import PCA pca = PCA(n_components=X_train.shape[1]) pca.fit(X_train) pca.explained_variance_ratio_ plt.plot([i for i in range(X_train.shape[1])], [np.sum(pca.explained_variance_ratio_[:i+1]) for i in range(X_train.shape[1])]) plt.show()

可以看到前40个维度,(注意不是X_train的前40个维度的特征,是降维后,新的坐标系的前40个坐标轴,即第一主成分到第四十主成分),已经可以表达接近100%的原始信息了.
PCA降维后,我们的数据不像原始数据那样具有可解释性了. 这是PCA的一个缺点. 降维后,在数学的角度上我们可以通过$X=X^{(')}W_k$还原回去得到一个M*N的矩阵,但是这个X与原始的X已经不一样了,因为降维后一定是损失了信息的,所以说只是数学角度上可以还原回去.
PCA降维后,有些时候不但不会降低模型的训练效果,反而提升了训练效果,因为我们损失了一些信息,但是这些不重要的信息可能恰好是影响模型训练的噪音.
PCA的一个典型应用,人脸识别中提取特征脸.
from __future__ import print_function
from time import time
import logging
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.datasets import fetch_lfw_people
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from sklearn.decomposition import PCA
from sklearn.svm import SVC
print(__doc__)
# Display progress logs on stdout
logging.basicConfig(level=logging.INFO, format='%(asctime)s %(message)s')
# #############################################################################
# Download the data, if not already on disk and load it as numpy arrays
lfw_people = fetch_lfw_people(min_faces_per_person=70, resize=0.4)
# introspect the images arrays to find the shapes (for plotting)
n_samples, h, w = lfw_people.images.shape
# for machine learning we use the 2 data directly (as relative pixel
# positions info is ignored by this model)
X = lfw_people.data
n_features = X.shape[1]
# the label to predict is the id of the person
y = lfw_people.target
target_names = lfw_people.target_names
n_classes = target_names.shape[0]
print("Total dataset size:")
print("n_samples: %d" % n_samples)
print("n_features: %d" % n_features)
print("n_classes: %d" % n_classes)
# #############################################################################
# Split into a training set and a test set using a stratified k fold
# split into a training and testing set
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.25, random_state=42)
# #############################################################################
# Compute a PCA (eigenfaces) on the face dataset (treated as unlabeled
# dataset): unsupervised feature extraction / dimensionality reduction
n_components = 150
print("Extracting the top %d eigenfaces from %d faces"
% (n_components, X_train.shape[0]))
t0 = time()
pca = PCA(n_components=n_components, svd_solver='randomized',
whiten=True).fit(X_train)
print("done in %0.3fs" % (time() - t0))
eigenfaces = pca.components_.reshape((n_components, h, w))
print