机器学习笔记 多项式回归

上一篇机器学习笔记里,我们讲了线性回归.线性回归有一个前提：即我们假设数据是存在线性关系的. 然而,理想很丰满,现实很骨感,现实世界里的真实数据往往是非线性的.

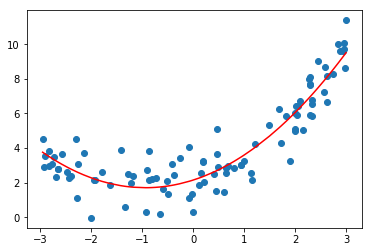
比如你的数据分布,是符合y=0.5$x^2$ + x + 2的.

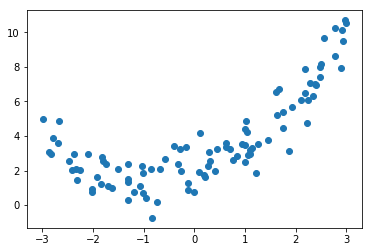
那你用y=ax+b去拟合,无论如何都没法取的很好的效果.

这时候,我们又想继续用上一篇笔记描述的线性回归来解决这个问题,我们要怎么办呢？一个很直观的想法就是,我们想造出一个新的特征$x^2$。那么现在我们拥有了2个特征x,$x^2$，我们就可以把问题转换为求解y=a$x^2$ + bx +c，从而把问题转换成我们熟悉的线性回归问题.

 

通过上面的分析,我们可以看出,我们想做的事情是对样本做升维(即增加样本的特征数目),sklean中完成这一功能的类叫做PolynomialFeatures.

class sklearn.preprocessing.PolynomialFeatures(degree=2, interaction_only=False, include_bias=True)

degree : integer

The degree of the polynomial features. Default = 2.

interaction_only : boolean, default = False

If true, only interaction features are produced: features that are products of at most degreedistinct input features (so not x[1] ** 2, x[0] * x[2] ** 3, etc.).

include_bias : boolean

If True (default), then include a bias column, the feature in which all polynomial powers are zero (i.e. a column of ones - acts as an intercept term in a linear model).

假设你的样本,原本有两个特征[a,b],那么当你进行一次degree=2的升维之后,你将得到5个特征[1,a,b,$a^2$,ab,$b^2$]，其中1又可以看做是$a^0或者b^0$。

关于degree的理解你可以参考一下下面这个例子.from sklearn.preprocessing import PolynomialFeatures

x=pd.DataFrame({'col1': [2], 'col2': [3],'col3':[4]})
print(x)
poly2 = PolynomialFeatures(degree=2)
poly2.fit_transform(x)

>>> array([[ 1.,  2.,  3.,  4.,  4.,  6.,  8.,  9., 12., 16.]])

poly3 = PolynomialFeatures(degree=3)
poly3.fit_transform(x)

>>> array([[ 1.,  2.,  3.,  4.,  4.,  6.,  8.,  9., 12., 16.,  8., 12., 16.,
        18., 24., 32., 27., 36., 48., 64.]])

  poly4 = PolynomialFeatures(degree=3,interaction_only=True)
  poly4.fit_transform(x)

>>> array([[ 1.,  2.,  3.,  4.,  6.,  8., 12., 24.]])

我们的样本有3个特征,值分别为2,3,4,degree=2时,可能的取值有$2^0$,$3^0$,$4^0$(均为1),$2^1,2^2,3^1,3^2,4^1,4^2$,$2*3,2*4,3*4$共10个值.

degree为3时,又新增了$2^3,3^3,4^3$，$2^2*3,2^2*4,3^2*2,3^2*4,4^2*2,4^2*3,2*3*4$共10个.总计20个.

interaction_only=true时,表示新增的特征存在交互性,不存在自己*自己,比如[2,3,4]的交互式输出是[2*3,2*4,3*4,2*3*4].

从上面的分析可以看出来,随着degree的增加,PolynomialFeatures新生成的特征数目是呈指数级别增加的.这将带来模型训练速度的严重下降和模型的过拟合,所以实际上一般很少用多项式回归.

 

---

 

来个具体的例子

import numpy as np  
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures

x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100)

#升维,为样本生成新的特征
poly = PolynomialFeatures(degree=2)
poly.fit(X)
X2 = poly.transform(X)

#对新样本做训练
from sklearn.linear_model import LinearRegression
lin_reg2 = LinearRegression()
lin_reg2.fit(X2, y)
y_predict2 = lin_reg2.predict(X2)

plt.scatter(x, y)
plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')
plt.show()