机器学习笔记 逻辑回归

逻辑回归

逻辑回归和线性回归其实有不少类似的地方,不同的是逻辑回归的$\hat y$是离散的.线性回归的$\hat y$是连续的.

逻辑回归：拟合样本数据发生的概率,根据概率进行分类处理.

逻辑回归,拟合样本发生的概率.
$\hat p = f(x)$,之后根据概率的大小对样本做分类.

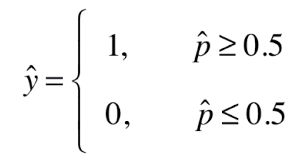
通常,将逻辑回归用来解决分类问题.作为分类算法时,解决的是二分类问题.

在线性回归一文中,我们知道$\hat y = \theta ^T X_b$,但是这个值的取值范围是负无穷到正无穷,如果我们想要表达概率的话,希望找到一个函数,取值范围在0-1.

Sigmoid函数

在一文读懂svm中,我们也提到过这个函数,是常见核函数的一种.以后在讲神经网络的时候也会再看到它.

$\hat p = \sigma(X_b \theta) =\frac 1 {1+e^{-X_b \theta}}$

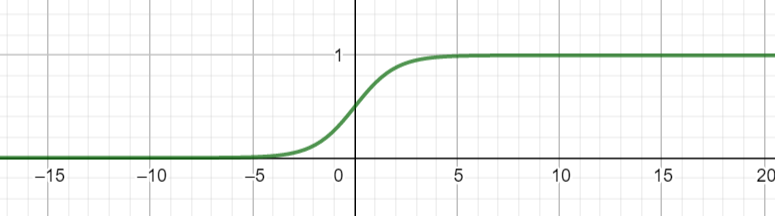
这个函数,我想不用多解释了,学过高中数学的应该都能明白其取值在0-1之间.

通过这个函数,我们可以把一个预测值转化为概率值,所以逻辑回归的概率模型可以表达为$$\hat p = \frac 1 {1+e^{-\theta ^T X_b}}$$.

我们做这样一个假设.

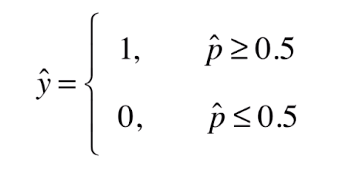
这样当有一个样本x过来,我们可以先计算出$\hat p$，再进而得到一个$\hat y$。

那么此时我们的问题转变为：怎样求得这样的$\theta$，使得我们预测的$\hat y$与真实的y之间误差最小？

 

损失函数

由于我们的$\hat y$有两种情况,是二元的,离散的.所以我们的损失函数也分两种情况

怎么理解？当y=1时,p越小,我们越倾向于把$\hat y$归为0. 这时候错的越离谱.   当y=0时,p越大,我们越认为$\hat y$归为1.

 

符合上述描述的损失函数可以表达如下：

 

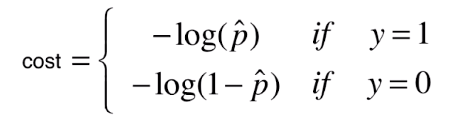
转换为统一的表达形式：

上面是单个样本的cost，这样对一个有着m个样本的系统来说,损失函数可以表达为：

即：

 

求损失函数的梯度

推导不困难,但是有点复杂.......

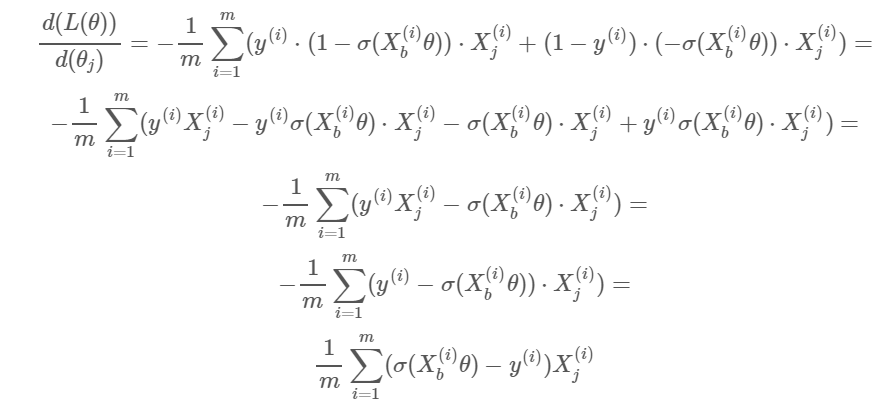
即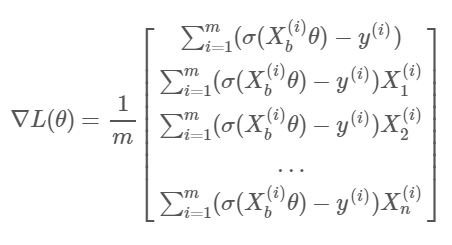，和我们在线性回归中算出的梯度形式很像.

 

有了梯度,就可以用梯度下降法求出使得$J(\theta)$最小的$\theta$。