卷积神经网络CNN

卷积神经网络，在图像识别和自然语言处理中有很大的作用,讲cnn的中文博客也不少,但是个人感觉说的脉络清晰清晰易懂的不多.

无意中看到这篇博客,写的很好,图文并茂.建议英文好的直接去看原文.英文不好的就直接看我这篇,算是读后总结吧.原文里对数学原理的着墨不多,在这篇文章里我会留着相关的标题,待日后慢慢补充这篇文章.

 

卷积神经网络

 

以上是一个cnn的典型结构.包含以下3种结构

• 卷积层
• 池化层
• 全连接层

卷积层

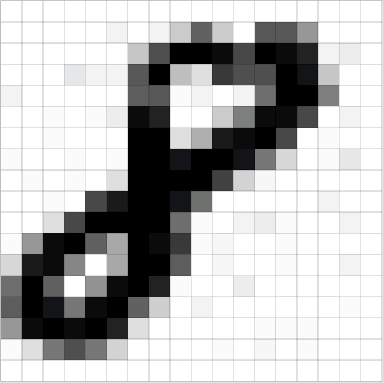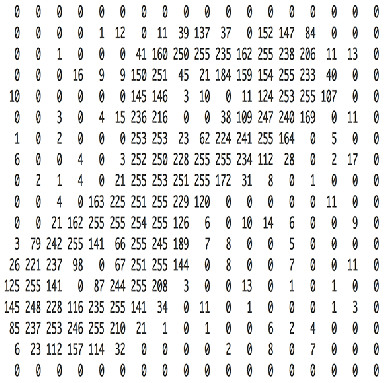
这是数字8的图片,图片其实就是一堆像素点的组合,可以理解为一个M*N的矩阵,矩阵中每一个元素的值就是像素值,取值从0-255.彩色的图有RGB三个通道,可以理解为3个M*N矩阵.为了简化讨论,我们以灰度图为例,灰度图是单通道的.

卷积在做什么

假设我们有一个5*5的图片

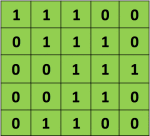
我们有一个3*3的矩阵,在CNN中,我们称之为‘filter‘ or ‘kernel’ or ‘feature detector’。

,

我们用这个kenel对输入的图像做卷积,过程如下所示：

其中,卷积的过程,用filter与input的相应位置相乘再相加.得到新的矩阵的对应元素的值.

然后滑动这个filter矩阵,滑动x个像素,x称之为步长stride(在这个例子中步长=1),算出下一个矩阵对应元素的值.不断重复这个过程. 完整过程如下所示:

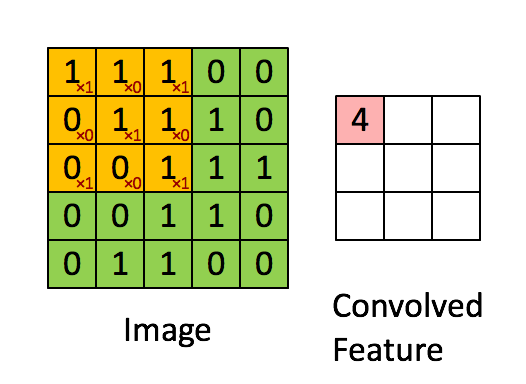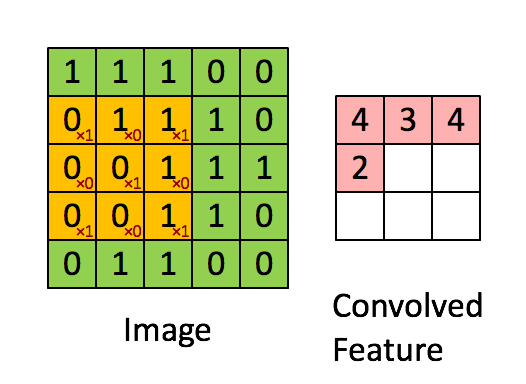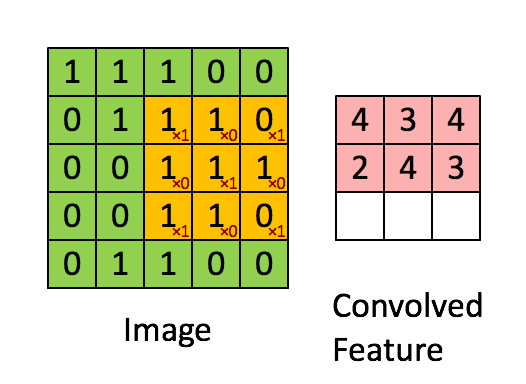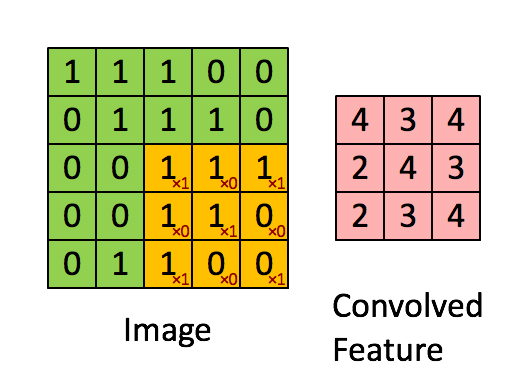
卷积后得到的这个3*3的矩阵称之为‘Activation Map’ or the ‘Feature Map‘.

卷积层完成了特征提取.

 

卷积有什么效果

不同的filter有不同的效果.比如上图展示了边缘检测,锐化,模糊等等.

下图很好的展示了cnn卷积操作做了什么：

不同的filter提取出了图片的不同角度的特征，得到了不同的特征图.注意将上述的图片都理解为一个一个的矩阵.

It is important to note that the Convolution operation captures the local dependencies in the original image.

影响我们得到的特征图的参数有以下几个：

Depth：

depth与filter数量是一致的.不同的独立的filter提取出不同的特征. 比如如下,有3个filter对原始图片进行处理,得到的特征图可以理解为3个叠在一起的矩阵.

 

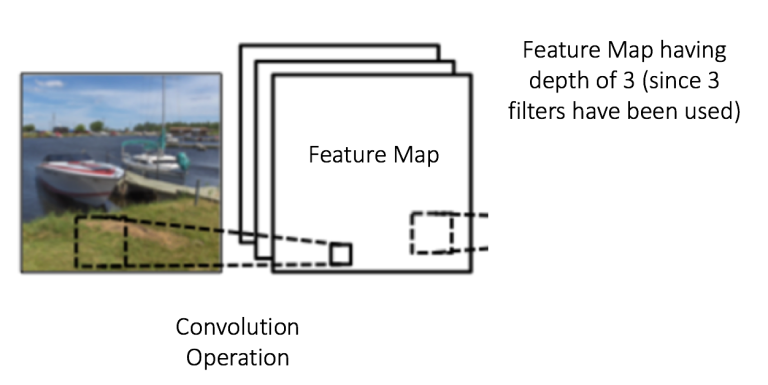
Stride

步长是filter矩阵在输入矩阵上每次滑动的距离.步长越大,最终得到的特征图越小.

Zero-padding 

补零操作,在原始矩阵周围补0. 添加补0的卷积叫wide convolution, 不添加补0的卷积叫 narrow convolution. 

以原始图像为32*32，filter为5*5为例,不做补0的话,得到的特征图矩阵大小为28*28.在神经网络的前几层,我们希望保留尽可能多的信息,好提取更多的特征.即我们希望依然得到一个32*32的矩阵.

https://adeshpande3.github.io/A-Beginner%27s-Guide-To-Understanding-Convolutional-Neural-Networks-Part-2/

Now, let’s take a look at padding. Before getting into that, let’s think about a scenario. What happens when you apply three 5 x 5 x 3 filters to a 32 x 32 x 3 input volume? The output volume would be 28 x 28 x 3. Notice that the spatial dimensions decrease. As we keep applying conv layers, the size of the volume will decrease faster than we would like. In the early layers of our network, we want to preserve as much information about the original input volume so that we can extract those low level features. Let’s say we want to apply the same conv layer but we want the output volume to remain 32 x 32 x 3. To do this, we can apply a zero padding of size 2 to that layer. Zero padding pads the input volume with zeros around the border. If we think about a zero padding of two, then this would result in a 36 x 36 x 3 input volume.

 

卷积为什么有这种效果

卷积为什么可以提取特征,背后的数学原理,日后补充

非线性(ReLU)

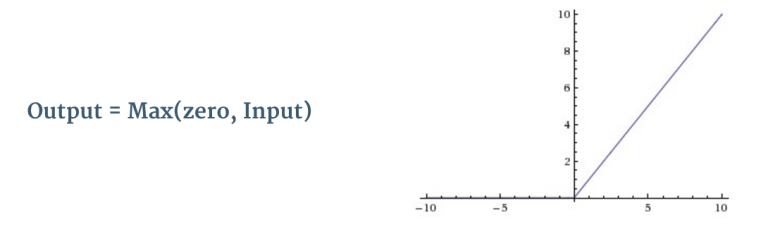
ReLU作用于卷积后得到的特征图. 将矩阵中的负数替换为0.

ReLU为卷积神经网络引入非线性.真实世界里的数据绝大多数是非线性的（卷积是一种线性操作）

The purpose of ReLU is to introduce non-linearity in our ConvNet, since most of the real-world data we would want our ConvNet to learn would be non-linear (Convolution is a linear operation – element wise matrix multiplication and addition, so we account for non-linearity by introducing a non-linear function like ReLU)

对特征图中的每一个像素做ReLU操作后的效果如上图所示.

其他的非线性函数还有tanh,sigmoid。但是实际使用中,大多情况下ReLU效果更好.

 

池化层

上面经过多个filter卷积,以及ReLU处理之后,我们得到了多个特征图.
此时我们想减小特征矩阵的维度,但是又保留下最重要的特征.和上面介绍的卷积过程类似,我们定义一个空间池.池化操作有Max, Average, Sum etc.

Spatial Pooling (also called subsampling or downsampling) reduces the dimensionality of each feature map but retains the most important information. Spatial Pooling can be of different types: Max, Average, Sum etc.

下图展示了用一个2*2的filter做最大池化后的效果:

下图展示了实际的特征图做不同的池化操作的效果：

 

池化有以下4个作用

• 减少特征维度
• 减少参数及运算量,这样模型的复杂度降低,避免过拟合
• 使得神经网络对原始图像的一些小改变可以无视,仍然取的相同的处理效果.  比如原始图片的某个像素从0-->10.假设这个像素周边的像素最大值为20.那做完max池化操作后,我们得到的仍然是20.
• 让我们得到等变的图像.(这句没大理解啥意思).作用就是：无论图片中的物体位于什么位置,我们都能识别.

• makes the input representations (feature dimension) smaller and more manageable  
• reduces the number of parameters and computations in the network, therefore, controlling overfitting [4]  
• makes the network invariant to small transformations, distortions and translations in the input image (a small distortion in input will not change the output of Pooling – since we take the maximum / average value in a local neighborhood).  
• helps us arrive at an almost scale invariant representation of our image (the exact term is “equivariant”). This is very powerful since we can detect objects in an image no matter where they are located (read [18] and [19] for details).

 

全连接层

全连接层是一个在输出层使用了softmax激活函数的多层感知机.

什么是多层感知机

卷积层和池化层的输出的特征图矩阵,代表了输入图像的高层次特征(high-level features).全连接层使用这些高层次特征对输入图片进行分类.

除了用于分类,添加一个全连接层通常也是一种为特征组合添加非线性的方式.对分类任务来说,使用卷积和池化层输出的特征就已经能取得不错的结果,但是把这些特征组合到一起,效果会更好.

全连接层输出的分类概率之和为1.这是由softmax保证的.

什么是softmax

 

CNN的完整过程

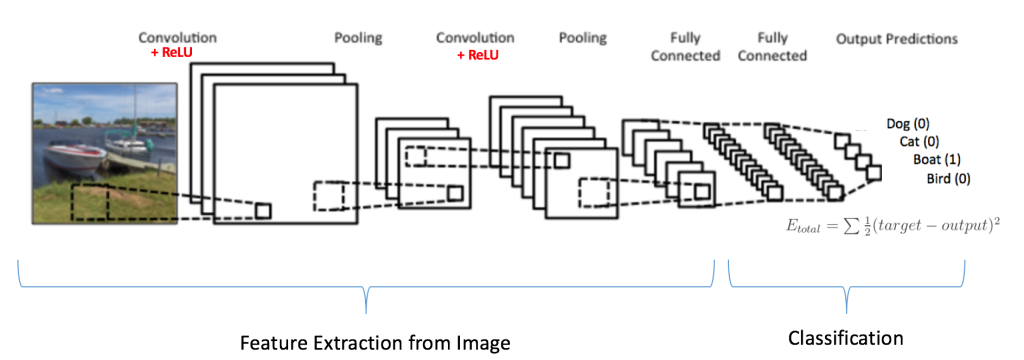
以上述图片识别为例,我们要识别出来这张图应该被分类为dog/cat/boat/bird?

上文说过了,卷积层和池化层的作用是特征提取,全连接层的作用是分类.

整个神经网络的训练过程如下：

• step1:用随机值初始化所有的filter和参数/权重
• step2:CNN接收待识别图片作为输入,经过卷积,ReLU,池化,全连接层的一系列操作后,可以输出分类概率
  • 比如我们得到概率为[0.2, 0.4, 0.1, 0.3]
  • 由于权重值是随机设置的,所以第一次训练后得到的分类概率也是随机的.
• step3:计算分类结果的错误.
  • 　 Total Error = ∑  ½ (target probability – output probability) ²
• step4:用反向传播算法计算Total Error 对网络中所有权值的梯度，利用梯度下降更新所有filter/权重值和参数值，使输出误差最小。
  • 　　权重根据它们对总误差的贡献按比例进行调整
  •        对同一图片再进行训练,这时候得到的概率可能是[0.1, 0.1, 0.7, 0.1]，距离正确的目标[0, 0, 1, 0]又更近一步了.这说明神经网络通过调整weights/filters的值已经更好地学到了图片的信息.
  •        在训练过程中,filters,filter size，cnn的结构这些是在step1之前就确定的,不会在训练过程中改变.只有filter矩阵的值和连接的权重会更新.
• step5:对训练集中的所有图片重复step2-step4.

这样我们的神经网络的filter/parameters/weights这些就确定下来了,当来了一个新的图片,我们就可以按照前面说的卷积-池化-全连接这个过程处理图片对其进行分类.

 

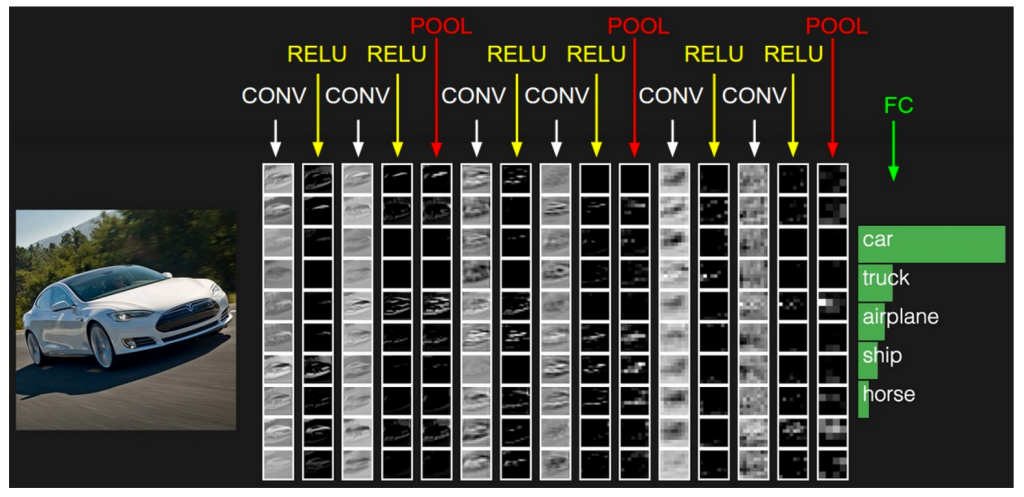
几点要注意的：

• 上面的例子里我们使用了2个卷积层+池化层,实际上这个次数是没有限制的.
• 并不是一定要一个卷积层接一个池化层,池化层前面可以有多个卷积层.

 

 手写数字识别示例

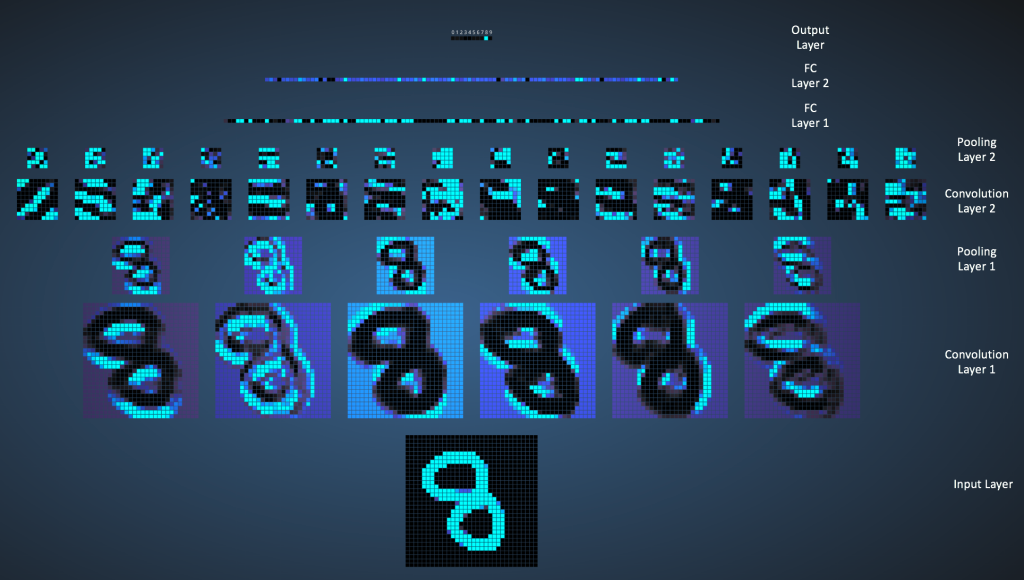
这是一个1024个像素点(32*32)的图片。

卷积层1有6个filter，每个filter是5*5矩阵(stride=1)。 28*28

池化层1做2*2 max pooling(stride=2)。            

可以看出来做max pooling之后,图片留下了最亮的点.

卷积层2有6个filter，每个filter是5*5矩阵(stride=1)。

池化层2做2*2 max pooling(stride=2)。

 

接下来是3个全连接层

• 第一个连接层有120个神经元
• 第二个连接层有100个神经元
• 第三个连接层(也叫输出层),有10个神经元,代表数字0-9.

 

---

 

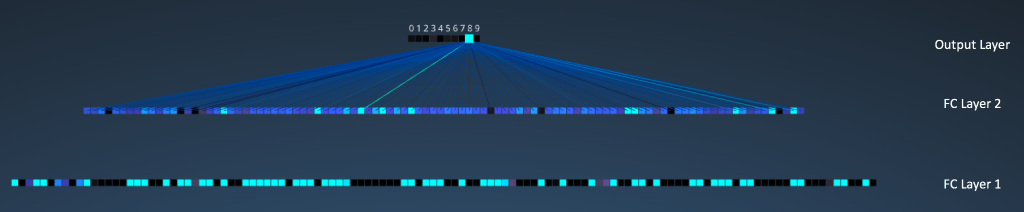
cnn识别手写数字集

model = Sequential()

model.add(Conv2D(filters = 32, kernel_size = (5,5),padding = 'Same',activation ='relu', input_shape = (28,28,1)))
model.add(Conv2D(filters = 64, kernel_size = (5,5),padding = 'Same', activation ='relu'))
model.add(MaxPool2D(pool_size=(2,2)))
model.add(Flatten())
model.add(Dense(256, activation = "relu"))
model.add(Dropout(0.2))
model.add(Dense(10, activation = "softmax"))

model.compile(optimizer = "SGD" , loss = "categorical_crossentropy", metrics=["accuracy"])

model.fit(X_train, Y_train, batch_size=100, verbose=1,epochs=5,validation_data=(X_val, Y_val))

完整代码见https://github.com/sdu2011/nlp/blob/master/keras.ipynb.