使用seaborn探索泰坦尼克号上乘客能否获救
titanic数据集是个著名的数据集.kaggle上的titanic乘客生还率预测比赛是一个很好的入门机器学习的比赛.
数据集下载可以去https://www.kaggle.com/c/titanic/data.
本身写这个系列笔记是作为自己机器学习的记录,也为了加深自己对机器学习相关知识的理解.但是写了前两篇seaborn的笔记以后,感觉缺乏实际的比赛数据的例子,写起来比较枯燥,读的人看的可能也很枯燥,浏览量也寥寥.读的人可能看完了会有一种，"哦，这样啊，原来如此,懂了懂了",然鹅,一拿到真实的数据,还是一筹莫展,无从下手.
所以,今天就拿真实的数据来学习一下seaborn要怎么用.怎么在开始正式的机器学习算法之前探索我们的数据关系.
titanic数据集给出了891行，12列已经标记的数据.即我们已知train.csv中891名乘客是否生还.我们需要预测test.csv中的418名乘客是否能够生还.
首先看一眼我们的数据.
| Variable | Definition | Key |
|---|---|---|
| survival | Survival | 0 = No, 1 = Yes |
| pclass | Ticket class | 1 = 1st, 2 = 2nd, 3 = 3rd |
| sex | Sex | |
| Age | Age in years | |
| sibsp | # of siblings / spouses aboard the Titanic | |
| parch | # of parents / children aboard the Titanic | |
| ticket | Ticket number | |
| fare | Passenger fare | |
| cabin | Cabin number | |
| embarked | Port of Embarkation | C = Cherbourg, Q = Queenstown, S = Southampton |
意思是一名名字叫harris的22岁男性乘客,乘坐三等仓,船上有1个兄弟姐妹/配偶,0个父母/子女,在Southampton上船,票价7.25,在此次灾难中没有生还.
拿到数据,我有几个简单的设想
- 票的级别越高,越容易获救 其实就是有钱有地位的容易获救
- 票价越高越容易获救 同上
- 兄弟姐妹或者父母子女多,容易获救 因为可以互相帮助
- 女性更容易获救
- 孩子更容易获救
好了,下面用seaborn来画画图,观察一下我们的数据,看看我拿到数据后第一想法对不对.
我主要用catplot 和 displot来绘图.
先来看看Pclass和Survived的关系.
catplot顾名思义,主要用来绘制分类数据(Categorical values).kind表示绘制什么样的图,bar,box,violin等等.
sns.catplot(x="Pclass",y="Survived", kind="bar", data=titanic_train);
以此为例,我们的数据集中Pclass的取值共有3种,1,2,3,分别表示一等票,二等票,三等票.
当我们选择bar图时,y轴绘制出的是一个矩形,表示的是"Survived"这个数据的均值.(默认是均值,也可以调整为中位值).由于我们的Survived取值只有0(遇难了),1(获救了).那么均值等于获救比例.
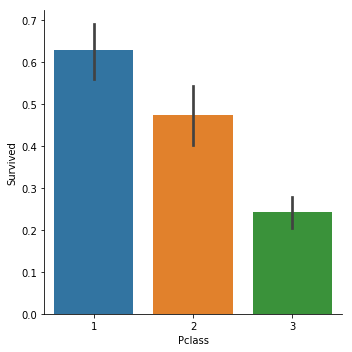
很明显1等票的生还率更高.
再来看下票价和生还之间的关系.
票价的数据各种各样,不像Pclass就3种.
sns.catplot(y="Fare",x="Survived", kind="bar", data=titanic_train);
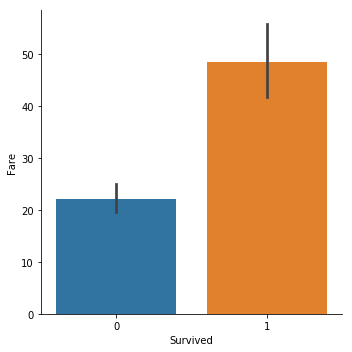
很明显,获救的人平均票价更高.
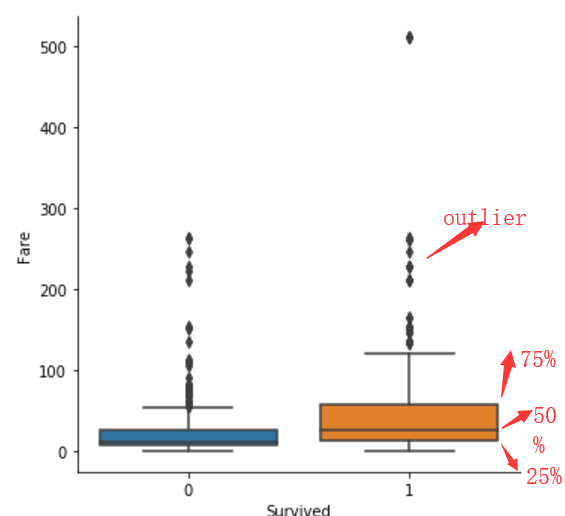
fare的值很多,我们想看看具体有哪些,大致的分布,可以用box.
sns.catplot(y="Fare",x="Survived", kind="box", data=titanic_train);
box绘图,会绘制出一个箱体,并标注出数据的25%（Q1）,50%(Q2),75%(Q3)及outlier处的位置.
其中怎么判断哪些点是属于异常值呢？根据IQR=Q3-Q1. 距离Q1或Q3的距离超过1.5IQR的就算是异常.
比如,下图的Q1=12 Q2=26 Q3=57.那么IQR=Q3-Q1=45. 超过Q3+1.5IQR=57+67.5=124.5的就会被算成异常点.会用黑色的小菱形绘制出来.
如果我们想要绘制出概率估计图.则可以用displot，或者kdeplot.这个在之前的文章里介绍过了.
sns.kdeplot(titanic_train["Fare"][(titanic_train["Survived"] == 1) & (titanic_train["Fare"].notnull())], shade=1, color='red')
sns.kdeplot(titanic_train["Fare"][(titanic_train["Survived"] == 0) & (titanic_train["Fare"].notnull())], shade=1, color='green');
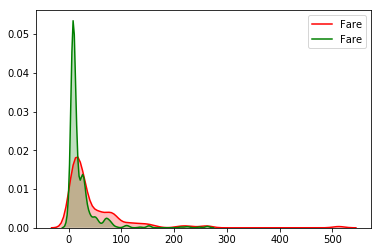
可以得到同样的结论,票价高的,获救概率更高一点.
注意:知识点来了
不止这一点,我们还看到,fare的分布并不是正态分布的,分布的极其不规则,也就是所谓的数据偏移,可以看到高收入的分布概率是很低的,但是高收入的样本分布确并不少,即假如我们把100认为高票价,一个人的票价是100以上的概率是很低的,但是在100-500之间分布的确很多,各种各样的都有.那机器学习算法在处理这个数据的时候就要注意了,要对数据做处理,可以用log函数做转换,或者你把0-20,20-50,50-100,100+的分别归类为1(很低),2(一般),3(较贵),4(很贵),用这种思想也可以.
实际上,对这个数据的处理,让我最终的预测率直接提高了2个百分点.
titanic_train["Fare"].skew()
可以通过这个skew()来检测数据的偏移度.如果数据偏移度比较高的话,如果skew()>0.75,一般需要对数据做分布变换,可以使用log变换.
这个skew()>0.75中的0.75怎么来的,我不太清楚,可能是一种经验值.我们的这个例子中skew()值已经接近5了.
下面来验证我们的猜想3,家人越多越容易得救
sns.catplot(x="SibSp",y="Survived", kind="bar", data=titanic_train);
sns.catplot(x="Parch",y="Survived", kind="bar", data=titanic_train);
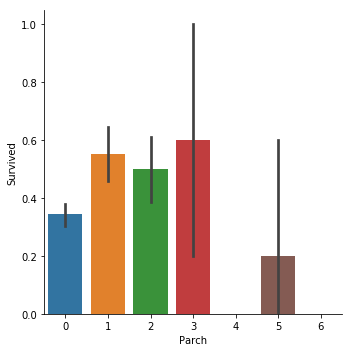
可以看到和我们的猜想并不一致,当有一个兄弟姐妹的时候,获救概率大概有0.55.而有4个兄弟姐妹的时候,获救概率反而只有0.15了.
在父母子女上,也是类似的,当父母子女达到5个的时候,获救概率反而低了.
titanic_train["family"] = titanic_train["SibSp"] + titanic_train["Parch"] + 1
sns.catplot(x="family",y="Survived", kind="bar", data=titanic_train);
我们创建一个新特征,家庭成员数,可以看到,当家庭人数比较少的时候,生还概率大.当家庭过于庞大,生还概率更低了.
猜想,是不是人少的时候,可以互相帮助,人多了,寻找家人会更困难,导致本可以获救的最终因为寻找家人也没活下来？
接下来看我们的猜想4,女人更容易获救
sns.catplot(x="Sex",y="Survived", kind="bar", data=titanic_train);
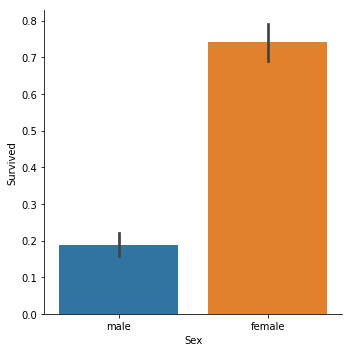
结论显而易见,女性获救概率高得多,lady first。
再来探索一下年龄与获救的关系,验证我们的猜想5.
sns.catplot(y="Age",x="Survived", kind="bar", data=titanic_train);
生还乘客的平均年龄是低了一点,但是两者区别不大,也都在正常区间,似乎看不出来什么.
我们来看看概率估计.
sns.kdeplot(titanic_train["Age"][(titanic_train["Survived"] == 1) & (titanic_train["Age"].notnull())], shade=1, color='red')
sns.kdeplot(titanic_train["Age"][(titanic_train["Survived"] == 0) & (titanic_train["Age"].notnull())], shade=1, color='green');
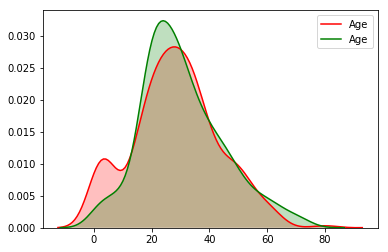
这个图就很明显了,在age很小的时候,红线(获救)明显有个波峰.说明在这个年级段,获救概率更高. 在age很大的时候(60岁以上),
绿线在红线之上,说明老人更可能遇难.
至此我们的5个猜想基本被验证,除了猜想3. 说明直觉还是比较准的嘛.
现在还剩下Name,Ticket,Cabin,Embarked这4个特征与Survived的关系没有验证.
其中Name,Ticket,Cabin都是不规则的字符串,需要做更多的特征工程,找到其中的规律以后,才好观察数据之间的关系.Embarked的取值只有S,C,Q3种.我们来看下Embarked与Survived的关系.
老套路：
sns.catplot(y="Survived", x = "Embarked",data = titanic_train, kind="bar")
C = Cherbourg, Q = Queenstown, S = Southampton
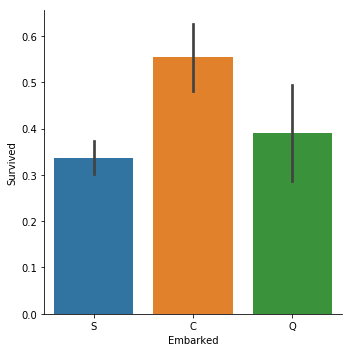
说实话,这个真的非常出乎我的意料.我原以为,是否生还和上船港口没有关系,三者的生还概率应该是基本一样才对.
然后我就开始胡思乱想了,总不能Cherbourg登船的人命好吧,越想越没道理.或者说Cherbourg登船的人都坐在船的某个位置，受到冰山撞击比较小？又或者只是因为样本数量太少了,是个偶然的巧合？
然后我想到是不是这个港口登船的都是有钱人？
sns.catplot(y="Fare", x = "Embarked",data = titanic_train, kind="bar")
sns.catplot(x="Pclass", hue="Embarked", data=titanic_train,kind="count")
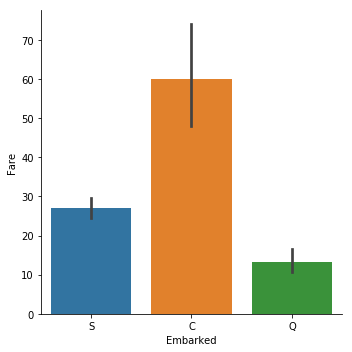
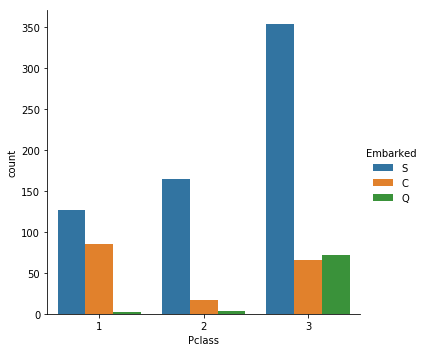
这么一看,还真是.所以Embarked=C的乘客生还概率高不是什么偶然.
所以这就引发了一个问题,数据之间其实有关联的,比如Embarked和Fare就有一定的相关性.我们可以用heatmap来探索各个特征数据之间的相关性.
sns.heatmap(titanic_train.corr(),annot=True,fmt ='.2f')
titanic_train.corr()计算出来的是各个特征的皮尔逊相关系数.皮尔逊相关系数。 wiki上解释一大堆,说实在的里面很多数学和统计学上的公式我没看懂.其实我们也不需要搞的特别清楚这些数学公式. 说白了,皮尔逊相关系数就是求两个向量之间的距离或者说夹角,越小越相关.(这个说法不严谨,但是原理上这么理解是没问题的).皮尔逊相关系数求出来在-1到1之间.
因为是求向量之间距离,所以展示的只有特征值是数字型的特征,Embarked特征的值是字符,所以没展示.你可以把字符映射成数字,比如S-->1,C-->2,Q-->3，再计算皮尔逊相关系数.当然这样做是有问题的.因为,S,C,Q本来不存在大小关系,这么映射以后存在了大小关系.这里涉及到一个one-hot编码问题.有兴趣的自己搜索一下,这篇就先不讲了.
ok,以上就是本篇文章使用seaborn探索titanic数据的内容,更多有趣有用的关于数据预处理可视化,关于seaborn使用等着大家去学习探索.希望这篇文章对大家有帮助和启发.
