DFS 序求 LCA
写在前面
DFS 序吊打欧拉序，赢！
定义
- DFS 序：表示对一棵树进行深度优先搜索得到的 结点序列
- 时间戳 DFN： 表示每个结点在 DFS 序中的位置。
算法内容
先给出结论：
不妨假设 \(\operatorname{dfn}(u)< \operatorname{dfn}(v)\)。
当 \(u\neq v\) 时，\(u, v\) 的 LCA 即为在 DFS 序中，处于 \([\operatorname{dfn}(u)+1, \operatorname{dfn}(v)]\) 之间深度最小的结点的父亲；
如果\(u=v\)，则它们的 LCA 即为 \(u\)
证明如下：
假设 \(\operatorname{dfn}(u)< \operatorname{dfn}(v)\)。 分类讨论：
1. 如果 \(u\) 不是 \(v\) 的祖先
记 \(\operatorname{LCA}(u, v)\) 为 \(u, v\) 的最近公共祖先。
令 \(d=\operatorname{LCA}(u, v)\)，DFS 的顺序显然为 \(d\rightarrow u\rightarrow d \rightarrow v\)。
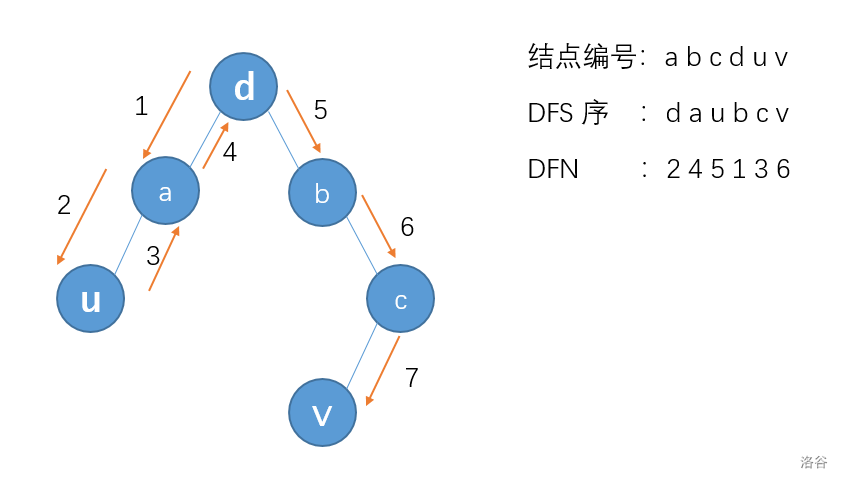
一个很重要的性质是： \(d\) 及其祖先不会出现在 \(u\rightarrow v\) 的 DFS 序中，这是易证的。
设 \(d\) 的儿子中，子树包含 \(v\) 的儿子为 \(v'\)（图中为 \(b\)）。显然，\(v'\) 应该在 \(u\rightarrow v\) 的 DFS 序之间。
这说明，我们只需要求在 \(\operatorname{dfn}(u)\) 到 \(\operatorname{dfn}(v)\) 之间深度最小的任意一个结点，其父亲即为 \(\operatorname{LCA}(u, v)\)。
2. 如果 \(u\) 是 \(v\) 的祖先
将查询区间从 \([\operatorname{dfn}(u), \operatorname{dfn}(v)]\) 变为 \([\operatorname{dfn}(u)+1, \operatorname{dfn}(v)]\) 即可。
容易发现，第二个区间也能满足情况 \(1\) 的正确性。
代码
本代码来自 Alex-Wei 的博客，仅根据个人码风习惯做了部分修改。
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 5e5 + 3;
int n, m, R, dn, dfn[MAXN], mi[19][MAXN];
vector<int> G[MAXN];
inline int get(int x, int y) {return dfn[x] < dfn[y] ? x : y;}
void dfs(int id, int f) {
mi[0][dfn[id] = ++dn] = f;
for(int it : G[id]) if(it != f) dfs(it, id);
}
inline int lca(int u, int v) {
if(u == v) return u;
if((u = dfn[u]) > (v = dfn[v])) swap(u, v);
int d = __lg(v - u ++);
return get(mi[d][u], mi[d][v - (1 << d) + 1]);
}
int main() {
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
cin >> n >> m >> R;
for(int i = 2, u, v; i <= n; ++ i) cin >> u >> v, G[u].push_back(v), G[v].push_back(u);
dfs(R, 0);
for(int i = 1; i <= __lg(n); ++ i) for(int j = 1; j + (1 << i) - 1 <= n; ++ j) mi[i][j] = get(mi[i - 1][j], mi[i - 1][j + (1 << i - 1)]);
for(int i = 1, u, v; i <= m; ++ i) cin >> u >> v, cout << lca(u, v) << endl;
}
写在最后（摘自 Alex-Wei 的博客）
对比 DFS 序和欧拉序，不仅预处理的时间常数砍半（欧拉序 LCA 的瓶颈恰好在于预处理，DFS 是线性），空间常数也砍半（核心优势），而且还更好写（对于一些题目就不需要再同时求欧拉序和 DFS 序了），也不需要担心忘记开两倍空间，可以说前者从各个方面吊打后者。
对比 DFS 序和倍增，前者单次查询复杂度更优。
对于 DFS 序和四毛子，前者更好写，且单次查询常数更小（其实差不多）。
对于 DFS 序和树剖，前者更好写，且单次查询复杂度更优（但树剖常数较小）。
将 DFS 序求 LCA 发扬光大，让欧拉序求 LCA 成为时代的眼泪！
