莫队学习笔记

蒟蒻终于开始学莫队了，为了印象深刻，写篇文章来及时复习

离线莫队

先丢个问题：给你一个序列长度为\(n\)，有\(m\)次询问，每次询问你\([l,r]\)这个区间内有多少个不同的数

很多数据结构都可以解决这个问题，但我们不用

先考虑怎么暴力，每次询问时对区间扫一遍，复杂度为\(O(nm)\)

这种暴力方法似乎不能优化，那么考虑换一种方法

用两个指针\(l,r\)分别指向\([l,r]\)这个区间的左端点和右端点，\(cnt[i]\)表示\(i\)这个数在\([l,r]\)这个区间的出现次数，画个图深刻理解下

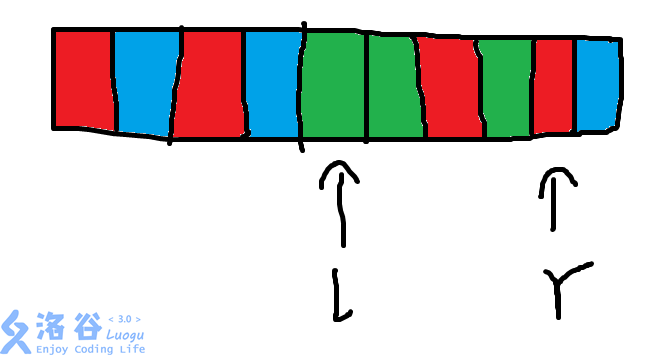
把数字用颜色来替代应该更容易看

现在\(l,r\)指向的这个区间内，\(cnt_{\text{绿}}=3,cnt_{\text{红}}=2,cnt_{\text{蓝}}=0\)，颜色种数\(tmp=2\)

我们把\(r\)指针往右移一个单位，\(r\)指向了蓝方块

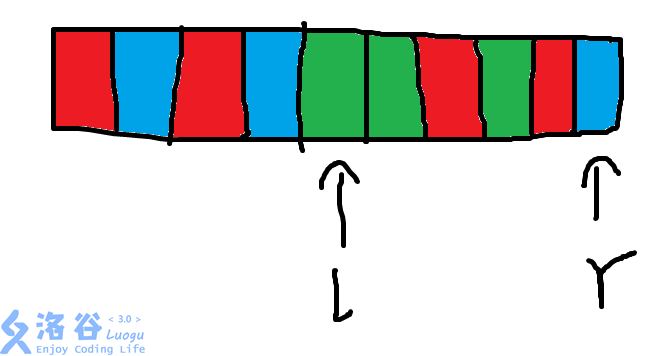
于是\(cnt_{\text{蓝}}=1\)，而蓝色在之前的区间没有出现过，所以相应的\(tmp\)也要\(+1=3\)，区间\([l,r]\)的颜色种数做出来了

这是扩大区间，对于缩小区间也是同理的，如果\(cnt_{\text{某个颜色}}\)减为\(0\)了，说明这个区间没有这个颜色，那么\(tmp\)也要\(-1\)

Part-Code

inline void add(int x)    //扩大区间
{
    tmp+=(++cnt[a[x]]==1);
}
inline void del(int x)     //减小区间
{
    tmp-=(--cnt[a[x]]==0);
}
while (l>q[i].l)add(--l);
while (r<q[i].r)add(++r);
while (l<q[i].l)del(l++);
while (r>q[i].r)del(r--);    //移动指针

但是这种暴力方法对时间复杂度并没有任何优化，仍然是\(O(nm)\)

我们考虑怎么优化

• 把操作都读下来，按左端点排序。不行，这样子仍然会被卡成\(O(nm)\)

• 将序列分成\(\sqrt n\)个长度为\(\sqrt n\)的块，对于左端点在同一个块里，将其按右端点排序，不在同一块里的按左端点排序。这样就保证了在每个块里的\(r\)指针都是向右移的，而\(l\)指针移超不过\(\sqrt n\)，所以时间复杂度为\(O(n\sqrt n)\)

Part-Code

int cmp(node x,node y)
{
    return ((x.l/blo)==(y.l/blo))?(x.r<y.r):(x.l<y.l);
}

• 然后还有一种卡常的排序方式——奇偶性排序，对左端点在同一个块里的询问，如果块的编号是奇数块，那么按升序排，偶数块则按降序排。这样排序的好处是在处理完左端点在一个块里的询问后，不用再从右移到左，所以理论上可以比上一个快一倍

Part-Code

inline int cmp(node x,node y)
{
    return (x.ll==y.ll)?((x.ll%2==1)?(x.r<y.r):(x.r>y.r)):(x.l<y.l);
}

• 最后想说的就是块的大小和时间复杂度是玄学的，所以没有必要非得是\(\sqrt n\)，对于随机情况来说，将块的大小定为\(\frac{n}{\sqrt{\frac{2m}{3}}}\)是快一点的

习题

1. P1972HH的项链

这道题是裸的莫队题，但是现在不卡常吸氧是过不去了

2. P2709小B的询问

这个是询问区间出现次数的平方和，只需要考虑一下平方的性质就好了

3. P3901数列找不同

题目每次问你区间内的数是否两两不同

还是一道很裸的板子题啊，更新答案时判断一下不同数的个数和区间长度是否相等就好了，这题暴力好像也能过

4. P4113采花

询问区间内出现两次以上的数的个数，但是这个数据范围莫队会t，可以当作莫队练练手

正解是树状数组，用维护出现一次的思想去想两次，一次的可以去做做P1972，总之多会几个方法比只会暴力好的啦

5. P4137mex

询问区间内未出现的最小自然数

这个题似乎跟之前的不太一样，但是由于数据水，我们仍然可以用莫队水过去

考虑加点，如果这个点没出现过，那么这个点会影响到答案，我们把答案每次\(++\)，暴力找到未出现过的

而删点的时候，如果这个点删去之后就没了，那么可以和答案取个\(min\)

复杂度，emmmm，很玄学，能过完全就是数据水

6. P3709大爷的字符串题

询问区间内的众数的出现次数

依旧维护每个数的出现次数，移动边界的时候注意一下众数个数不是唯一的，根据其性质更新答案就好了

7. P3674小清新人渣的本愿

三种询问，区间内是否存在两个数相加得\(x\)，两个数相减得\(x\)，相乘得\(x\)

不会bitset专门跑去学的

我们用\(bitset:S\)来维护区间内的数是否出现，拿\(A-B=x\)来说，移项变为\(A=x+B\)，也就是如果\(S\&(S<<x)\)不为零，说明可以

加法也同理，我们维护一个\(N-x\)的\(bitset\)，继续用这个思路来做

而对于乘法，因为一个数\(x\)的因子最大到\(\sqrt x\)，我们直接暴力枚举因子，看有没有出现就可以了

带修莫队

其实就是加了个一个单点修改的操作，而离线莫队肯定是不能带修改的，那么我们继续考虑如何处理修改操作

• 我们对每次询问区间\([l,r]\)加一个版本\(t\)，每次访问的也就是\([l,r,t]\)，\(t\)实际上是表示在第\(t\)次修改后的序列，处理的时候\(t\)和\(l,r\)一样跳就行了，要注意一点就是如果要跳到的版本的修改位置在\([l,r]\)中，要修改\(cnt_{a_{x}}\)

• 要对修改和查询操作分别存储，修改操作要记录当前修改的位置\(x\)的之前的颜色，这样便于返回上一个版本；查询操作多存一个时间\(t\)就好了

Part-Code

void jia1s(int x)      //到下一个版本
{
	if (l<=p[x].x&&r>=p[x].x)del(p[x].x);
	a[p[x].x]=p[x].z;   //更新
	if (l<=p[x].x&&r>=p[x].x)add(p[x].x);
}
void jian1s(int x)     //到上一个版本
{
	if (l<=p[x].x&&r>=p[x].x)del(p[x].x);
	a[p[x].x]=p[x].lx;
	if (l<=p[x].x&&r>=p[x].x)add(p[x].x);
}
while (t<q[i].t)jia1s(++t);
while (t>q[i].t)jian1s(t--);  移动t指针

• 排序跟离线的是差不多的，多了一点就是如果右端点在一个块里，要按\(t\)升序排序，同样的，这个排序也可以按奇偶性排序。

Part-Code

int cmp(node x,node y)   普通排序
{
    return (x.ll==y.ll)?(x.rr==y.rr?x.t<y.t:x.r<y.r):x.l<y.l;
}
int cmp(node x,node y)   奇偶性排序
{
	return (x.ll==y.ll)?((x.rr==y.rr)?(x.t<y.t):((x.ll%2==1)?(x.r<y.r):(x.r>y.r))):(x.l<y.l);
}

• 块的大小的话一般选取\(n^{\frac{2}{3}}\)，块的个数就是\(n^{\frac{1}{3}}\)，左右端点所在块的种数都为\(n^{\frac{1}{3}}\)，然后和单个块的移动复杂度\(O(n)\)乘起来之后复杂度就是\(O(n^{\frac{5}{3}})\)

习题

1. P1903数颜色

裸的带修莫队，当然也可以树套树

卡卡常，吸个氧才能过，数据对莫队太不友好了

树上莫队

原来我们的莫队是处理线性结构，这次把它搬到了树上，那么做法是否一样呢？

其实是基本上一样的，只不过我们要把树转化为线性结构，这就需要欧拉序，我们从根对这棵树进行\(dfs\)，点进栈时记一个时间戳\(st\)，出栈时再记一个时间戳\(ed\)，画个图理解一下

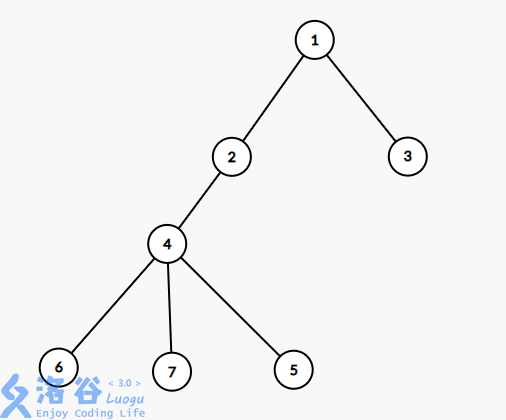
这棵树的欧拉序为\((1,2,4,5,5,6,6,7,7,4,2,3,3,1)\)，那么每次询问的节点\(u,v\)有两种情况

1. \(u\)在\(v\)的子树中（\(v\)在\(u\)的子树中同理），比如\(u=6,v=2\)，我们拿出\((st[2],st[6])\)这段区间\((2,4,5,5,6)\)，\(5\)出现了两次，因为搜索的时候\(5\)不属于这条链，所以进去之后就出去了，而出现一次的都在这条链上，就都可以统计

2. \(u\)和\(v\)不在同一个子树中，比如\(u=5,v=3\)，这次拿出\((ed[5],st[3])\)这段区间\((5,6,6,7,7,4,2,3)\)，要保证\(st[u]<st[v]\)，出现两次的可以忽略，然而这次只统计了\(5,4,2,3\)，所以最后再统计上\(lca\)就好了

• 至于如何忽略掉区间内出现了两次的点，这个很简单，我们多记录一个\(use[x]\)，表示\(x\)这个点有没有被加入，每次处理的时候如果\(use[x]=0\)则需要添加节点；如果\(use[x]=1\)则需要删除节点，每次处理之后都对\(use[x]\)异或\(1\)就可以了

• 上面说的欧拉序之类的东西都可以用树剖做出来，然后就做完了

• 因为\(st,ed\)的大小都是\(n\)，所以取块的大小时要用\(2n\)，而不是\(n\)

习题

1. SP10707COT2

裸的树上莫队，注意下权值很大要离散化就好了

2. P4689[Ynoi]这是我自己的发明

由乃oi题个个都很毒瘤

询问两个点子树中权值相等的数对个数，支持换根操作

首先我们要知道还完根后对于一个点\(x\)，我们应该如何去找其子树，有三种情况：

我们默认树根是\(1\)，每次记录下换的根\(rt\)

• \(x=rt\)，子树是整棵树

• \(lca(x,rt)\ne x\)，直接访问\(x\)的子树

• \(lca(x,rt)=x\)，子树为与\(x\)的相邻的点中和\(rt\)最近的点的补集

既然已经会处理换根的操作，那么询问也就很好做了

我们用\(f_{l,r\cap L,R}\)来表示\(l-r\)与\(L-R\)这两个区间的答案，\(f_{1,n\cap1,i}\)可以预处理出来，然后对于不同种情况，大力容斥一波，剩下的只需要求\(f_{l,r\cap L,R}\)，转换成\(4\)个莫队求解就可以了

树上带修莫队

其实只需要把树上莫队和带修莫队结合起来就好了，然后要注意一点

• 在更新版本的时候，我们不能像以前一样判断在不在\([l,r]\)这个区间内更新值，而是看这个位置有没有被选，这应该非常好理解

Part-Code

void jia1s(int x)     //到下一个版本
{
	if (use[p[x].x])   //被选了
	{
		calc(p[x].x);
		a[p[x].x]=p[x].z;
		calc(p[x].x);
	}
	else a[p[x].x]=p[x].z;
}
void jian1s(int x)    //到上一个版本
{
	if (use[p[x].x])   //被选了
	{
		calc(p[x].x);
		a[p[x].x]=p[x].lx;
		calc(p[x].x);
	}
	else a[p[x].x]=p[x].lx;
}

• 取块的大小注意下是\(2n\)就好了，排序什么的跟之前是一样的

习题

P4074糖果公园

这个题询问树上两点路径之间\(\sum_i\sum_jV_i\times W_j\)，\(i\)为出现的糖果的种类，\(j\)为出现的次数，所以很显然就是用莫队维护了

注意一下统计答案时的操作就好了

---

如果有其他莫队的题我会慢慢放上来的QAQ