洛谷 P4779 【模板】单源最短路径（标准版）

一个蒟蒻简单地说下这道题

题目

给你一个有向图，求出从这个点到其他所有点的最短路径（边权不为负）

思路

一看到最短路，就想到了spfa和dijkstra算法，于是随随便便就写了出来。

---

dijkstra怎么写？

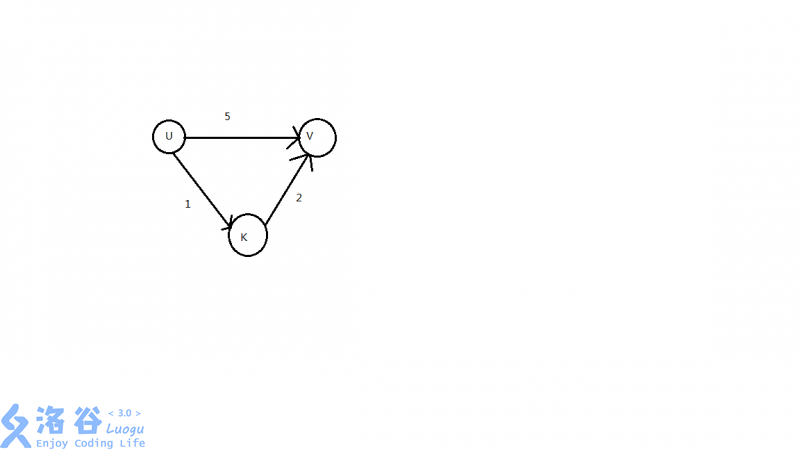
在一个有向图中，我们从起点出发，找出和它的距离最小（也就是dis）的点，再取出所有与这个点相连的边，做一遍松弛。

什么是松弛？

如果从点u到点v的路径中，有一个中转点k使得k.cost+dis[v}<dis[v]，那么就刷新dis[v]，即dis[v]=k.cost+dis[v]。

这样子dijkstra的时间复杂度为O(n^2)。

代码如下

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
struct edge
{
    int to,cost;
};
int n,m,st,dis[100001],vis[100001];
vector <edge> s[100001];
vector <edge>::iterator it; 

int main()
{
    cin>>n>>m>>st;
    for (int i=1;i<=n;i++)
    	dis[i]=2147483647;
    edge a;
    int b;
    for (int i=1;i<=m;i++)
    {
        cin>>b>>a.to>>a.cost;
        s[b].push_back(a);
    }
    dis[st]=0;
    for (int i=1;i<=n;i++)
    {
        int zd=2147483647,k=0;
        for (int j=1;j<=n;j++)
            if (!vis[j]&&dis[j]<zd)
            {
                zd=dis[j];
                k=j;
            }
        if (k==0)
            break;
        vis[k]=1;
        for (it=s[k].begin();it!=s[k].end();it++)
            if (dis[k]+(*it).cost<dis[(*it).to])
                dis[(*it).to]=dis[k]+(*it).cost;
    }
    for (int i=1;i<=n;i++)
        cout<<dis[i]<<" ";
    return 0;
}

---

可是

关于spfa，它死了

在一些数据中很容易被卡掉，所以就不具体介绍了，如果想写spfa可以去P3371。

TLE！

这是为什么呢，我们看下数据，n<=1e5,如果单纯的跑dijkstra，而时间复杂度是O（n^2），所以肯定会T。

我们考虑下对于每次找出与起点相连的dis最小的点，时间复杂度为O(n),能不能优化呢？当然是可以。

堆

这就要用到了我们万能的堆，用堆访问最小的dis时间复杂度为O（log（n）），所以堆优化dijkstra的时间复杂的为O（(m+n)log（n）），这个题就够用了。而这并不能掩盖我不会写别种的优化的事实。

代码如下

#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <utility>
using namespace std;
struct edge
{
	int to,cost;
};
struct cmp
{
	int u,d;
	bool operator<(const cmp &a) const
	{
		return d>a.d;
	}
};
int n,m,st,vis[100001];
vector <edge> s[100001];
vector <edge>::iterator it;
priority_queue <cmp> dis;
int main()
{
    cin>>n>>m>>st;
    dis.push((cmp){st,0});
    for (int i=1;i<=n;i++)
    	vis[i]=2147483647;
	edge a;
	int b;
	for (int i=1;i<=m;i++)
	{
		cin>>b>>a.to>>a.cost;
		s[b].push_back(a);
	}
	vis[st]=0;
	dis.push((cmp){st,vis[st]});
	while (!dis.empty())
	{
		cmp k=dis.top();
		dis.pop();
		if (vis[k.u]!=k.d)
			continue;
		for (it=s[k.u].begin();it!=s[k.u].end();it++)
			if (vis[k.u]+(*it).cost<vis[(*it).to])
			{
				vis[(*it).to]=vis[k.u]+(*it).cost;
				dis.push((cmp){(*it).to,vis[(*it).to]});
			}
	}
	for (int i=1;i<=n;i++)
		cout<<vis[i]<<" ";
    return 0;
}

蒟蒻的第一篇题解，码风不好，讲的也不清楚，希望大家多多包涵。