Trie与可持久化Trie
经过两天的奋斗,我终于点满了Trie树的技能树
Trie树(字典树)
顾名思义,对于一个字符串,将其各个字符建成树,其中包含一定的父子关系(第\(i\)个字符是第\(i+1\)个字符的父亲),像这样,当对若干个字符串进行建树操作时,两两字符串的公共部分就会沿着树走下来,在不同处分叉,这个显然是很好理解的。
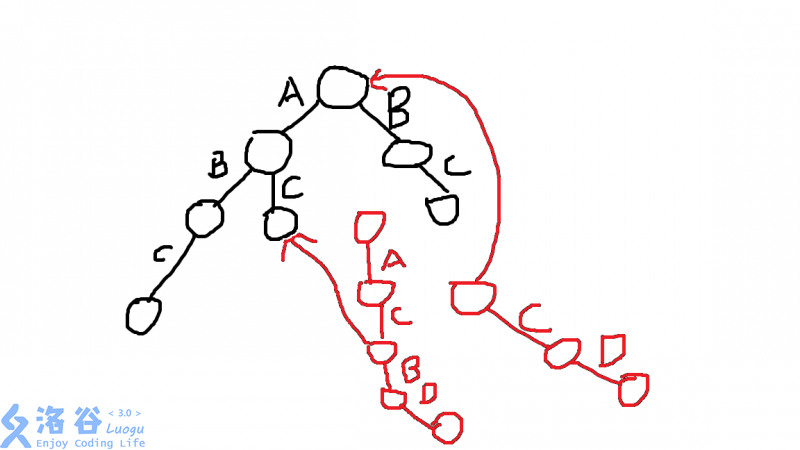
我们看着个图,原先的Trie树已经有了\(ABC\),\(AC\),\(BC\)这三个串(根节点为空)。当要插入\(CD\)这个串时,由于原来的树没有以\(C\)为字节点的子树,那么就只能将这个串插到根节点下面;而插入\(ACBD\)这个串时,由于原树已经有了一条\(AC\)的路径,那么我们只需要把\(BD\)接到\(C\)后面即可。
这个操作看起来简单,其实用代码实现起来也是很简单的。
int insert(char *ch) //trie[u][x]表示u节点的x字符指针指向的节点
{
int u=0,l=strlen(ch+1);//u为初始指针指向根节点
for (int i=1;i<=l;++i)
{
int x=ch[i]-'A'; //每次取出字符串中的第i位
if (!trie[u][x])trie[u][x]=++tot; //如果Trie中没有x这个节点,那就插进去
u=trie[u][x]; //往下走
}
p[u]=1; //给结尾打标记
return 0;
}
那么查询操作也是同理,从选取字符串的每一位,从树根往下遍历就可以了。
int query(char *ch)
{
int u(0),l=strlen(ch+1);//u位初始指针指向根节点
for (int i=1;i<=l;++i)
{
int x=ch[i]-'A'; //取出
if (!trie[u][x])return 0; //指针指向空,表示匹配不成功,直接退出
u=trie[u][x]; //往下走
}
return p[u]; //返回结尾标记值
}
时间复杂度:单次\(O(l)\)。空间复杂度:\(O(\sum_{i=1}^{N}l[i]*B)\)(\(B\)为字符集大小)
习题
给出\(N\)个字符串,看是否有一个串\(A\)为串\(B\)的前缀。
因为我们在Trie树插入操作中已经对每一串字符串都打上了标记,所以满足答案的关系只有两种,一种是插入的串是之前的串的前缀,那么只要看在插入过程中是不是没有新增节点,另一种是插入的串包括之前的串,也就是之前的串是插入的串的前缀,这个只要看看有没有走到打了标记的点就好了。
完整代码 把清空写炸了害我交了好几次
给出\(N\)个单词,和\(M\)个句子,问每个句子中包含这些单词的最长前缀是多少。
考虑对着\(M\)个单词建一个Trie树,\(f[i]\)表示前\(i\)个字符是否可行,便可以每次访问\([j+1,l](0\leq j< l)\),在访问过程中访问到标记,就可以直接更新\(f[i]\),复杂度\(O(NM)\).
完整代码 不在\(query\)函数中更新\(f[i]\)复杂度是\(O(N^2M)\),会TLE!
给出\(N\)个01串,和\(M\)个01串,问这\(M\)个串的每一个串中满足和这\(N\)个串其中的一个串有着相同的前缀(前者是后者的前缀或后者是前者的前缀)。
再用一个数组\(q[u]\)来记录经过\(u\)节点有多少个01串,用\(p[u]\)来记录以\(u\)节点结尾的01串有多少个,我们先每次往后访问,用\(p[u]\)来更新\(ans\),答案显而易见也只有两种可能,一种是走到一个指向空的节点,这时候只要返回\(ans\)就好了,另一种是这个串包含了路径上的所有串,这时要返回\(ans+q[u]-p[u]\)(因为有重复计算,这个自己模拟下感性理解就好了)。
完整代码 没啥好说的emmmm
01Trie
Trie树就只能对着字符串一顿胡乱操作?答案肯定不是。有一类题,让你求出一些数中\(A\oplus B\)的最大值。我们很容易想到用枚举暴力去求,但是复杂度\(O(N^2)\)着实让人受不了,于是就可以用01Trie进行求解。
就拿刚才的题目——最大异或数对来说,考虑把所有的数转成二进制插入Trie树中,那么接下来有一种贪心的策略:因为对于两个二进制数,只有这一位上不同,也就是一个是\(0\)一个一个是\(1\)才会取\(1\),否则取\(0\),那么在找数的过程中贪心的走和当前位相反的那一位,如果相反那一位指向空,就只能走下面这一位,这样子就找到了序列中和这一个数最大的异或值,只需要从\([1,N]\)的各个数找一个最大的答案即可。
这样说太抽象,我们看下面这张图:
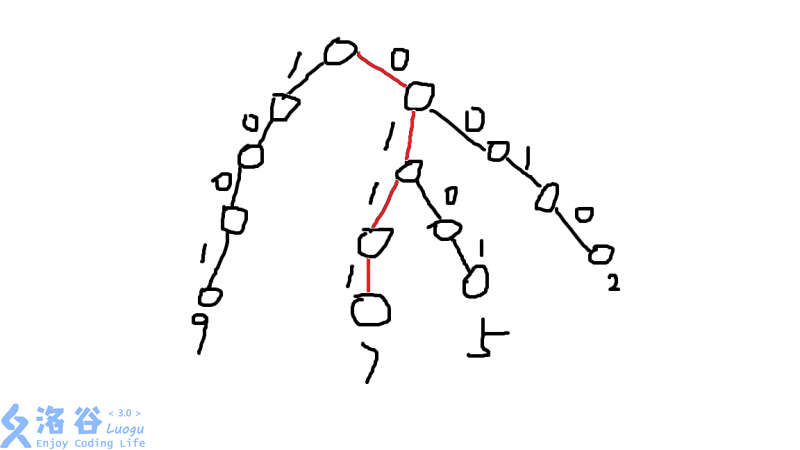
我们把\(9(1001)\),\(7(0111)\),\(5(0101)\),\(2(0010)\)依次插入树中(最高位补足0),当我们要找和\(9\)异或的最大值,只需要贪心的走反路就可以啦,没有反路那就只能往下走了。感性理解感性理解
而由于题目的数据一般会比较大,我们需要建一个\(30\)位的01Trie。
代码实现起来也很简单
int query(int x)
{
int u(0),an(0); //an记录当前数x与序列中的数的异或最大值
for (int i=30;i>=0;i--) //从高到低位走
{
int ch=(x>>i)&1; //取出
if (trie[u][!ch])u=trie[u][!ch],an+=1<<i;
//如果可以走反路,就走反路,更新an
else u=trie[u][ch]; //走不了就只能往下走了
}
return an;
}
时空复杂度:单次\(O(log\text{值域})\),总共\(O(Nlog\text{值域})\),已经可以满足很多题的需要了。
完整代码 一定要按题目数据来开树的长度!
习题
在一个有\(N\)个元素的序列\(A\)中,找出\((A[l1]\oplus A[l1+1]\oplus …\oplus A[r1])+(A[l2]\oplus A[l2+1]\oplus…\oplus A[r2])\)的最大值,其中,\(1\le l1\le r1<l2\le r2\le N\)。
设\(l[i]\)表示\(1\le l\le r\le i\),最大的\(A[l]\oplus A[l+1]\oplus…\oplus A[r]\),\(r[i]\)表示\(i\le l\le r\le N\)最大的\(A[l]\oplus A[l+1]\oplus…\oplus A[r]\),那么答案为最大的\(l[i]+r[i+1]\)。
我们首先要知道一个异或的性质:对于一个序列\(A\)的区间\([l,r]\),都有\(A[l]\oplus A[l+1]\oplus…\oplus A[r]=(A[1]\oplus A[2]\oplus…\oplus A[l-1])\oplus(A[1]\oplus A[2]\oplus…\oplus A[r])\)
于是设\(x[i]\)表示\(A[0]\oplus A[1]\oplus…\oplus A[i](A[0]=0)\),所以\(l[i]=max(x[i]\oplus x[j])(0\le j<i)\),\(r[i]=max(x[i]\oplus x[j])(i<j\le N)\)
然后这个题就很好做啦。
完整代码 数组开大千万别RE
给定一棵\(N\)个点的带权树,结点下标从\(1\)开始到\(N\)。寻找树中找两个结点,求最长的异或路径。(异或路径指的是指两个结点之间唯一路径上的所有边权的异或)
题意感性理解好了
先\(dfs\)跑出所有节点到根节点的异或路径丢进\(xorr\)数组中,问题便转化成了求最大的\(xorr[i]\oplus xorr[j](i,j\in N,i\ne j)\),是不是似曾相识呢,没错,这道题就变成了最大异或数对啦!
完整代码 我竟然写炸了快读???
可持久化数据结构——主席树
主席树?????这个Trie有什么关系吗?别着急,当然是有关系啦。没关系我也不会去学啊(大雾
主席树,全名可持久化线段树,是一种支持对历史版本修改和访问的数据结构,主要思想就是对其每个版本都建一棵线段树。
然而这样子空间和时间都受不了,而我们想每次建新的线段树过程中,并不是所有元素都不一样,许多元素都是上个版本继承过来的,于是只要把这些碎片拼在一起,就是主席树了。
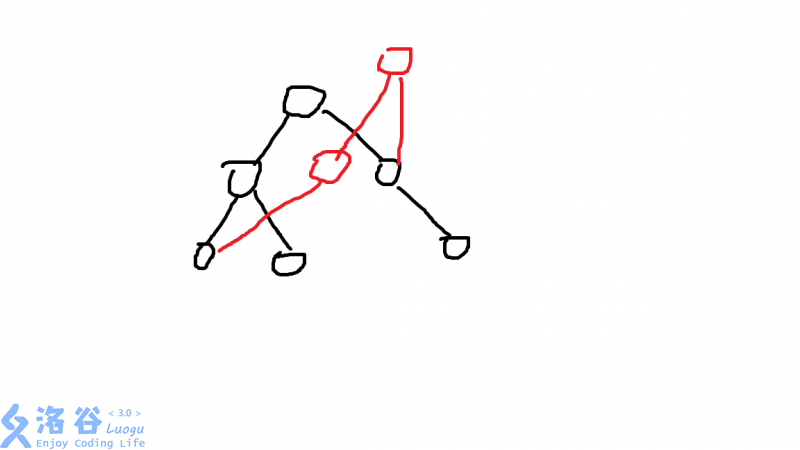
我们看这个图片,假设黑色的是第一个版本,红色的是第二个版本,也就是新的版本,当新建红色这个树时,只需要继承上个版本的一些元素,再修改并重新拼接元素就可以了,这样时空复杂度都是很优秀的。
板子题——可持久化数组
基本操作就拿这个题来说吧。
存储变量
struct ff
{
int lc,rc,val; //存放左子树,右子树,权值
}s[40000500];
int n,m,a[40000500],rt[40000500],node_cnt; //a表示序列,rt是根,node_cnt是节点数
建树
void build(int &k,int l,int r)
{
k=++node_cnt; //新的一个节点
if (l==r)
{
s[k].val=a[l];
return;
}
int mid=l+r>>1;
build(s[k].lc,l,mid); //更新左子树
build(s[k].rc,mid+1,r); //更新右子树
}
和线段树的建树方式差不了多少,就不详细说了。
修改
int change(int k,int l,int r,int x,int cnt)
{
int root=++node_cnt; //更新也要新建节点
s[root]=s[k]; //继承
if (l==r)
{
s[root].val=cnt; //点修改
return root;
}
int mid=l+r>>1;
if (x<=mid)s[root].lc=change(s[root].lc,l,mid,x,cnt); //更新左子树
else s[root].rc=change(s[root].rc,mid+1,r,x,cnt); //更新右子树
return root;
}
也和线段树是差不多的。
访问
int query(int k,int l,int r,int x)
{
if (l==r)return s[k].val; //点访问
int mid=l+r>>1;
if (x<=mid)return query(s[k].lc,l,mid,x);//如果在左边,就找左子树
else return query(s[k].rc,mid+1,r,x); //如果在右边,就找右子树
}
这就是主席树啦!是不是很简单。
完整代码 我再也不乱用没返回值的函数了,然后再次感谢评论区的大佬:qwaszx(dsq),Mital。
另一道板子题——可持久化线段树1
先对序列排序+离散化,然后在离散化的数组的基础下建一颗空的主席树,对于每一个区间\([1,i]\)插入到主席树,访问的时候只要将主席树\([1,r]-[1,l-1]\)就是区间\([l,r]\)了,推荐去看这篇博客,因为我不太会讲。还不是没理解
完整代码 数组一定不要开小了!
可持久化Trie
学完主席树,就可以学可持久化Trie啦,我们先看这道题——最大异或和
有一个序列\(A\),每次可以进行两种操作,一是在序列尾插入一个数,序列长度\(N\)变为\(N+1\),二是在区间\([l,r]\)中找到一个\(p\),满足\(l\le p\le r\),并使得\(A[p]\oplus A[p+1]\oplus…\oplus A[N]\oplus x\)最大,输出这个最大值。
首先,我们把这个式子拆开,也就变成了\((A[1]\oplus A[2]\oplus…\oplus A[N])\oplus(A[1]\oplus A[2]\oplus…\oplus A[p-1])\oplus x\),似乎很简单,但是这道题还有一个在末尾插入的操作,就需要我们用到可持久化Trie了。
其实可持久化Trie和主席树的思想是类似的,实现方式也有相同之处,就是对每一个前缀异或建一个01Trie,该继承的继承,该修改的修改,这样就完成了。
插入
void insert(int x)
{
int rt=root[node_cnt]; //取出上一个根节点的信息
root[++node_cnt]=++node; //新建节点
for (register int i=24;i>=0;i--)
{
int ch=(x>>i)&1; //取出
size[node]=size[rt]+1; //长度增加
trie[node][ch]=node+1; //给节点编号
trie[node][!ch]=trie[rt][!ch]; //继承上一个根节点的部分子树信息
rt=trie[rt][ch]; //往下走
node++;
}
size[node]=size[rt]+1;
}
访问
void query(int l,int r,int x)
{
int lc=root[l],rc=root[r],ans=0; //取出左右子树
for (register int i=24;i>=0;i--)
{
int ch=(x>>i)&1; //取出
if (size[trie[rc][!ch]]-size[trie[lc][!ch]]>0)
//如果反路有路可走
lc=trie[lc][!ch],rc=trie[rc][!ch],ans|=1<<i;
//走反路并更新答案
else
lc=trie[lc][ch],rc=trie[rc][ch];
//否则只能往下走
}
write(ans);
putchar(10);
}
时空复杂度:总共:\(O(31(N+M))\)
代码应该是比较好理解的
对于这个题,每次插入一次前缀异或,共\(N+\)访问中位添加操作的次数,访问时只要访问区间\([l-1,r]\)的答案就好了。
完整代码 不会卡常的我写了点奇怪的卡常+\(O2\)竟然跑到了最优解\(Rank57\)???
今年省选还考了一道Trie树的题——异或粽子,相信参加省选的dalao看到这么简单的题都切掉了,我这个初四蒟蒻反正看到题是不会做。
这道题其实是让你求在长度为\(N\)的序列\(A\)中,前\(K\)大的\(A[l]\oplus A[l+1]\oplus…\oplus A[r](1\le l\le r\le N)\),的和。
反正我刚开始是不会做,在dsq神仙的帮助和指点下,彻底的大彻大悟。
其实就是先对序列\(A\)进行一个前缀异或得到序列\(sum\),然后只要求\(K\)对最大的\(sum[i]\oplus sum[j](0\le i\le j\le N)\),就好了。
那么我们该怎么求呢,在我迷茫无助之时,dsq给我指点了道题序列合并。
拿这道题来说,我们要对序列\(A\),\(B\)升序排序,然后将\(A[i]+B[1]\)丢进小根堆中,每次取出堆顶,然后把\(A[i]+B[2]\)丢进去,如果丢过了,那就丢\(A[i]+B[3]\),同理往下,就做完啦。
回到这道题,仔细一样是不是和那道题的思想一样呢?我们用堆存值,编号(也就是\(i\))和第几大就好了。
可是怎么求第\(k\)大的值呢?我们依旧建一个01Trie,访问便用到了平衡树(然而我并不会平衡树)的思想,在建树的时候多存一个\(size[u]\)记录\(u\)的子树大小,在访问时看能不能走反路,如果可以走,那就要看看\(k\)和\(size[trie[u][!ch]]\)大小,如果\(k\le size[trie[u][!ch]]\),那么答案在反着的那条路径,我们就走,并更新\(ans\)值,否则答案就在不走反的那条路径,走,并且\(k\)要减去\(size[trie[u][!ch]]\),这个就很显然了。
也可以选择去看dsq的题解。
完整代码 一定要开longlong
字符串真是个美妙的东西,我感受到了真正的算法之美,等到5.5回学校巨想对班主任喊一声:“老东西,你教的文化课最没用啦!”


 浙公网安备 33010602011771号
浙公网安备 33010602011771号