BUAA北航面向对象OO第一单元总结

OO第一单元总结

目录

• OO第一单元总结
  • 前言
  • 第一次作业
    • 目标
    • HW1基本思路
    • UML类图
    • 代码规模
    • 复杂度分析
      • 方法复杂度
        • 分析
      • 类复杂度
        • 分析
    • 优化策略
  • 第二次作业
    • 目标
    • HW2基本思路
    • UML类图
    • 代码规模
    • 复杂度分析
      • 方法复杂度
        • 分析
      • 类复杂度
        • 分析
    • 优化策略
  • 第三次作业
    • 目标
    • HW3基本思路
    • UML类图
    • 代码规模
    • 复杂度分析
      • 方法复杂度
        • 分析
      • 类复杂度
        • 分析
    • 优化策略
  • 整体架构分析
  • 数据生成及自动化评测
    • 第一次作业
      • 数据生成
      • 代码示例
      • 自动化评测
    • 第二次作业
      • 数据生成
        • 代码示例
      • 自动化评测
        • 代码示例
    • 第三次作业
      • 数据生成
        • 代码示例
      • 自动化评测
  • 自我程序bug分析及测试手段
    • 自我程序bug分析
      • 第一次作业
      • 第二次作业
      • 第三次作业
    • 测试手段
      • 第一次作业
      • 第二次作业
      • 第三次作业
  • 他人程序bug分析
    • 第一次作业
    • 第二次作业
    • 第三次作业
  • hack别人程序bug策略
    • 第一次作业
    • 第二次作业
    • 第三次作业
    • hack策略分析
  • 心得体会
  • 鸣谢

前言

本次OO第一单元总结将从如下几个部分展开:

1.三次作业迭代开发思路

2.整体架构分析

3.自动化生成数据及自动化测评实现思路

4.自我程序bug分析及测试手段

5.他人程序bug分析

6.hack别人程序bug策略

7.心得体会

8.鸣谢

复杂度分析利用IDEA的MetricsReloaded插件，代码规格统计利用IDEA的static插件

第一次作业

目标

通过对表达式结构进行建模，完成单变量多项式的括号展开，初步体会层次化设计的思想

HW1基本思路

​ 虽然笔者在寒假较为充分地预习了JAVA，但在面对第一次作业时仍然感到有一点无从下手，感到难度巨大，尤其是在面对一种叫做“递归下降”的前所未闻的方法时，笔者一度认为笔者过不了中测。可是事实证明课程组对作业的安排和设置是合理的，在潜下心来研究递归下降法后，笔者发现这种方法并没有想象中的这么难，只是一种基于文法的递归调用。当要解析一个表达式的时候，可以递归下降解析表达式中的每一个项；当要解析项的时候，可以递归下降每一个因子。解析每一个因子的时候，根据当前的token解析分类解析每一个因子(幂函数，常数，表达式因子)。这样一来，利用递归下降便可以很自然地处理括号嵌套的情况。因此，从第一次作业到第三次作业，笔者都能狗处理嵌套括号的情况(自己有空玩玩(1+(1+x)**2)**2也挺爽的)

​ 在理解了这一点后，笔者又遇到了一个难点，应该采取什么数据结构来表示每个对象的状态？由于当时笔者仍然是面向过程思维(现在似乎也没有改善多少oao)，简单地采取了采用HashMap<Integer, BigInteger>来保存每个x的指数和系数，虽然对于第一次作业这是完全没有问题的，但是对于第二次作业便捉襟见肘，不得不重构了。

UML类图

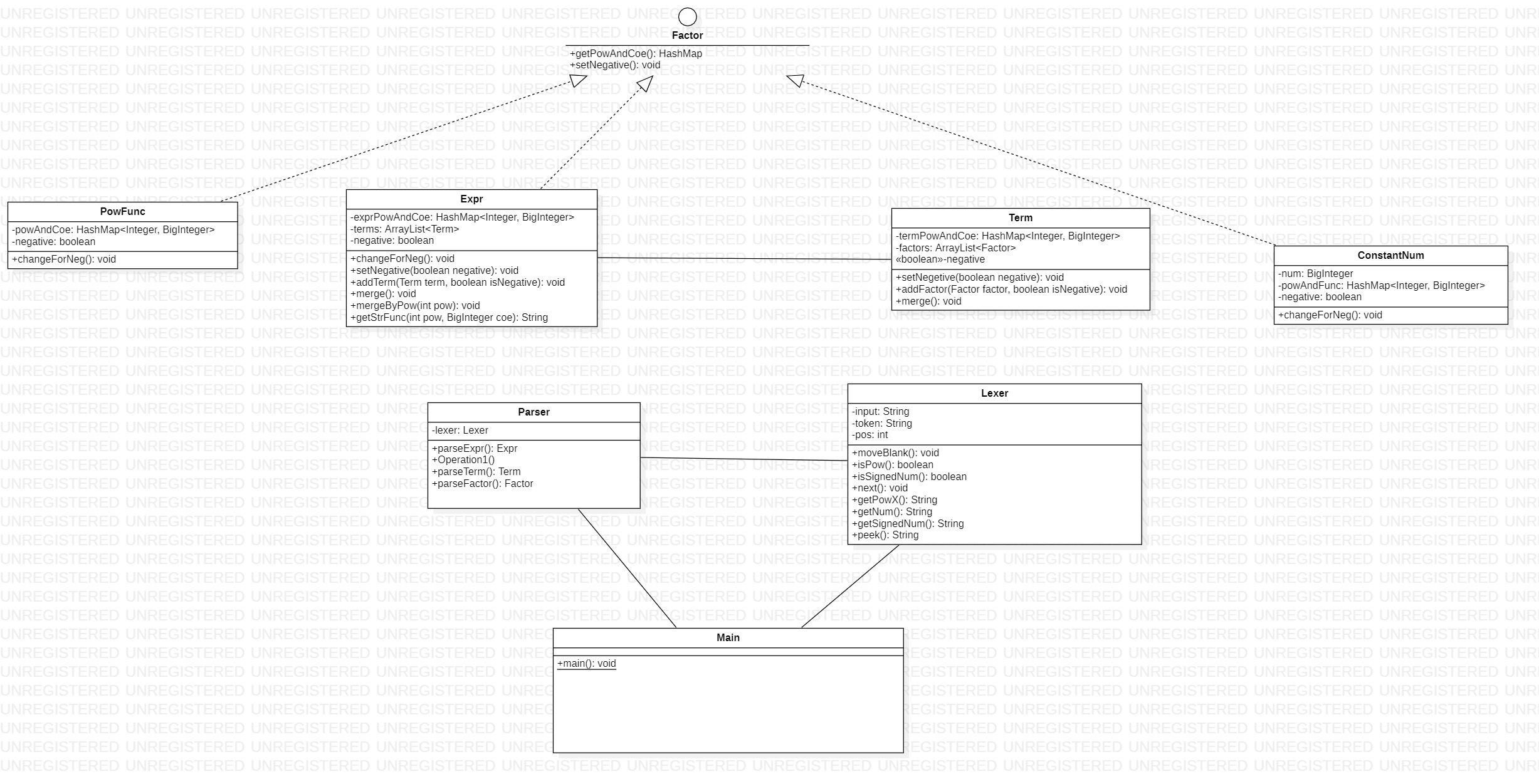
PowFunc、Expr、ConstantNum实现Factor接口便于实现多态进行递归调用，parser类依赖Lexer进行文法解析

代码规模

一共写了474行代码，似乎并不算多？

复杂度分析

方法复杂度

先解释一下ev(G)、 iv(G)、 v(G)的含义

ev(G)是基本复杂度，是用来衡量程序非结构化程度的，非结构成分降低了程序的质量，增加了代码的维护难度，使程序难于理解。因此，基本复杂度高意味着非结构化程度高，难以模块化和维护。实际上，消除了一个错误有时会引起其他的错误。

Iv(G)是模块设计复杂度，是用来衡量模块判定结构，即模块和其他模块的调用关系。软件模块设计复杂度高意味模块耦合度高，这将导致模块难于隔离、维护和复用。模块设计复杂度是从模块流程图中移去那些不包含调用子模块的判定和循环结构后得出的圈复杂度，因此模块设计复杂度不能大于圈复杂度，通常是远小于圈复杂度。

v(G)是圈复杂度，用来衡量一个模块判定结构的复杂程度，数量上表现为独立路径的条数，即合理的预防错误所需测试的最少路径条数，圈复杂度大说明程序代码可能质量低且难于测试和维护，经验表明，程序的可能错误和高的圈复杂度有着很大关系。

from: https://blog.csdn.net/weixin_30346033/article/details/97099084

Method	CogC	ev(G)	iv(G)	v(G)
ConstantNum.ConstantNum(String)	0	1	1	1
ConstantNum.changeForNeg()	3	1	3	3
ConstantNum.getPowAndCoe()	0	1	1	1
ConstantNum.setNegative(boolean)	0	1	1	1
Expr.Expr()	0	1	1	1
Expr.addTerm(Term, boolean)	0	1	1	1
Expr.changeForNeg()	3	1	3	3
Expr.getPowAndCoe()	0	1	1	1
Expr.getStrFunc(int, BigInteger)	11	3	7	8
Expr.merge()	3	1	3	3
Expr.mergeByPow(int)	7	1	5	5
Expr.setNegative(boolean)	0	1	1	1
Expr.toString()	8	1	5	5
Lexer.Lexer(String)	0	1	1	1
Lexer.getNum()	2	1	3	3
Lexer.getPowX()	5	1	4	4
Lexer.getSignedNum()	0	1	1	1
Lexer.isPow()	1	1	2	2
Lexer.isSignedNum()	1	1	3	3
Lexer.moveBlank()	3	2	2	4
Lexer.next()	8	2	6	7
Lexer.peek()	0	1	1	1
Main.main(String[])	3	3	2	3
Parser.Parser(Lexer)	0	1	1	1
Parser.parseExpr()	8	1	6	6
Parser.parseFactor()	11	4	6	6
Parser.parseTerm()	4	1	4	4
PowFunc.PowFunc(String)	2	1	2	2
PowFunc.changeForNeg()	3	1	3	3
PowFunc.getPowAndCoe()	0	1	1	1
PowFunc.setNegative(boolean)	0	1	1	1
Term.Term()	0	1	1	1
Term.addFactor(Factor, boolean)	0	1	1	1
Term.getPowAndCoe()	0	1	1	1
Term.merge()	14	1	7	7
Term.setNegetive(boolean)	0	1	1	1
Total	100.0	45.0	93.0	98.0
Average	2.78	1.25	2.58	2.72

分析

可以看到，整体的复杂度并不高。但可以发现其中Parser类的方法复杂度较高，这是因为parser类作为递归下降的分析器，大量调用了Expr，Term，Factor的方法(将某一项设置为负数)。这一点是当初写代码的时候考虑得不够周全的地方，应该把每一项设置为负数和parser类解耦。

类复杂度

同样先解释一下OCavg、OCmax、 WMC的含义

OCavg是类平均圈复杂度, 继承类不计入

OCmax应该是类最大圈复杂度

WMC是类总圈复杂度

Class	OCavg	OCmax	WMC
ConstantNum	1.5	3	6
Expr	3	7	27
Lexer	2.33	7	21
Main	3	3	3
Parser	4	6	16
PowFunc	1.75	3	7
Term	2.2	7	11
Total			91.0
Average	2.53	5.1	13.0

分析

同样可以看到，parser类的复杂度比较高，理由同上。

优化策略

第一次作业由于只包含多项式，因此优化较为简单，笔者采用HashMap<Integer,Biginteger>作为每个因子，项，表达式的基本项，保存指数和系数。

化简时根据HashMap的指数和系数来进行合并同类项，由于HashMap存的是基本类型，因此也就不存在深拷贝和浅拷贝的问题。

可以做的优化有x**2->x*x,把正项提到前面。

但由于笔者太懒了，没有把第一项前面的"+"去掉，导致答案为1的时候会输出+1，因此强测碰到这个点性能分一下子就全没了= =

第二次作业

目标

通过对表达式结构进行建模，完成多项式的括号展开与函数调用、化简，进一步体会层次化设计的思想

HW2基本思路

第二次作业在第一次作业的基础上增加了三角函数因子，自定义函数，求和函数等内容。

这样一来采用HashMap<Integer,Biginteger>作为每个因子，项，表达式的基本项的思路就完全行不通了,只能进行重构，笔者本来想用一个四元组作为基本项，每一个表达式，项，因子保存形如a*x**b*cos(x)**c*sin(x)**d的基本项，但这样一看就很不OO，并且在仔细阅读了指导书后，笔者发现还会有类似a*x**b*cos(x)**c*sin(x)**d*cos(x**e)**f*sin(x**g)**h这样的项，因此基本项的长度是不定的，所以这个方案也被否决了。为了更好地从第一次作业迭代到第二次作业，笔者最后决定新建一个类BasicTerm作为每个表达式，项，因子的基本项。

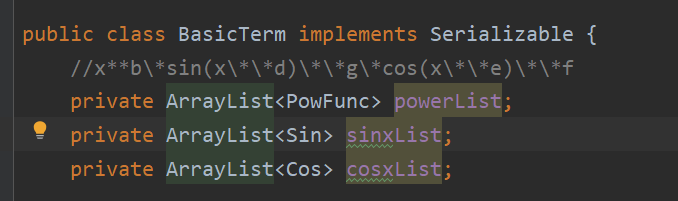
其中每个基本项有三个列表，保存幂函数，cos，sin因子，在BasicTerm中实现“BasicTerm相加运算”、“BasicTerm相乘运算”最后便可以类似作业一中使用HashMap<BasicTerm, BigInteger>化简(其中BigInter为每一个基本项的系数)。

对于文法解析器Parser和Lexer，由于第一次作业到第二次作业文法基本没有变化，所以不需要重构，只需要在Lexer增加对新增加的因子的解析，以及在Parser中实现对新增因子的递归下降即可。

对于新增的自定义函数，笔者的做法是字符串替换，即将对应的实参添加括号后替换到函数定义式中得到待解析的表达式，利用Parser和Lexer解析表达式，最后将解析完成的表达式返回。

对于新增的求和函数，笔者的做法也是字符串替换，先设置一个总表达式，然后将每个求和表达式中的i换成当前进行运算的数字，然后将"+替换后的表达式"加入到总表达式中，最后类似自定义函数对总表达式进行解析(现在看来似乎可以边代入边解析，而不必转化成一个总表达式再进行解析)，然后将解析完成的表达式返回。

可以看到，在笔者的实现中，自定义函数和求和函数这两个因子其实最后在输入表达式中的地位就是一个表达式因子，只不过解析的方法与表达式因子有所不同。同时，要实现笔者对自定义函数和求和函数的解析方法，要求程序能支持对嵌套括号的处理，而对于递归下降法，这一点也就是自然而然的了。

最后，关于结果的输出方法，笔者是在顶层Expr的toString递归调用每个Term的toString，每个Term递归调用因子的toString这样递归输出

UML类图

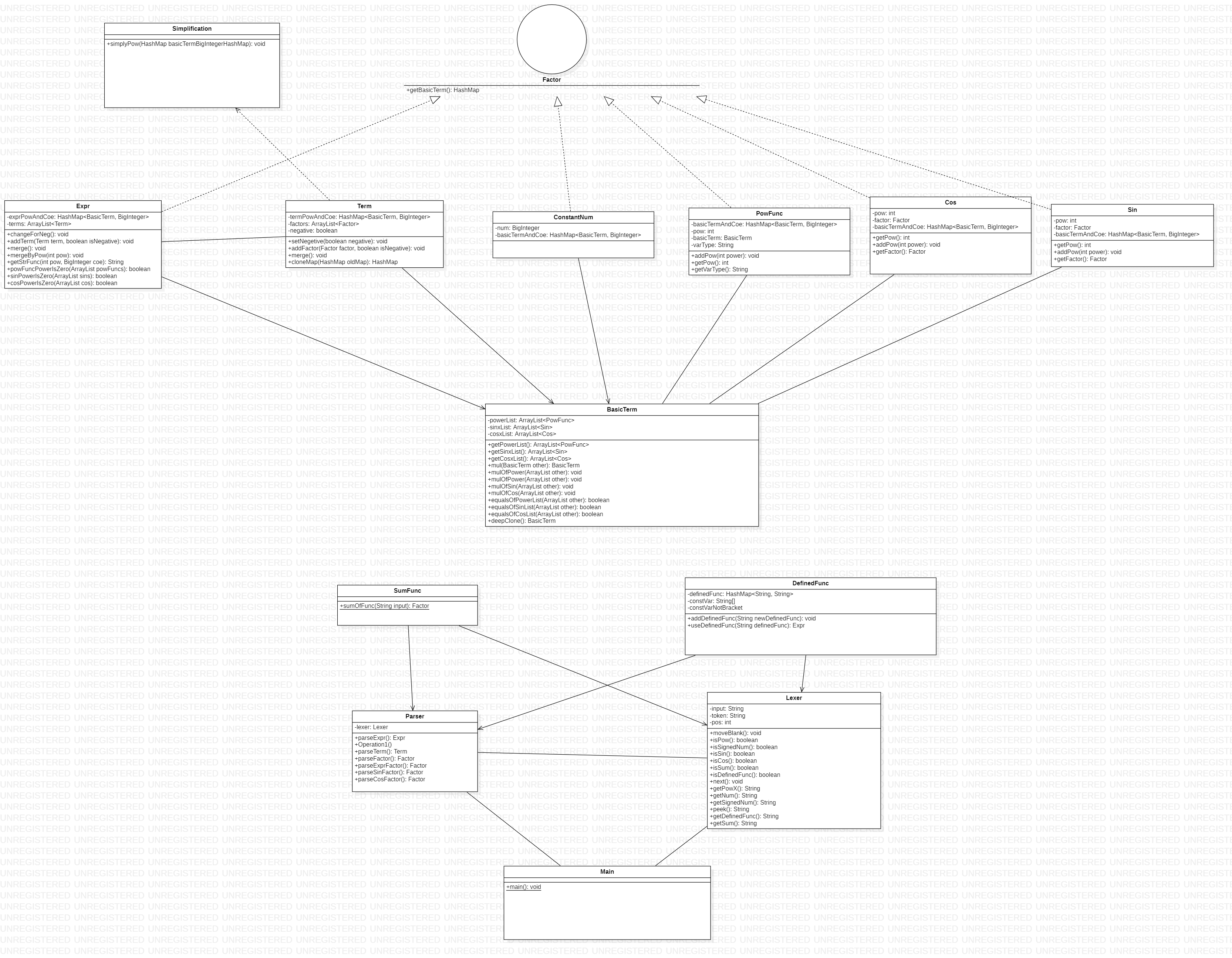
其中Expr， Term， ConstantNum， PowFunc， Cos， Sin实现了Factor接口，由于自定义函数和求和函数只是返回的是表达式因子，而本质上只是一种“解析方法”，故不作为Factor接口的实现。

同时Term依赖Simplification类的静态方法进行化简。

代码规模

对比于第一次作业的474行代码，第二次作业总共为1251行代码，几乎是第一次作业的三倍，可以看出HW1到HW2是一个巨大的飞跃。

如果说第一次作业是从0到1，那第二次作业就是从1到n

BasicTerm.java	215	199	0.9255813953488372	1	0.004651162790697674	15	0.06976744186046512

在所有类中BasicTerm类的行数最多，共有215行，原因是它作为基本项，需要实现乘、加、相等这些基本运算，因此代码行数较高

复杂度分析

方法复杂度

Method	CogC	ev(G)	iv(G)	v(G)
BasicTerm.BasicTerm(PowFunc, Cos, Sin)	3	1	4	4
BasicTerm.deepClone()	0	1	1	1
BasicTerm.equals(Object)	4	3	4	6
BasicTerm.equalsOfCosList(ArrayList)	10	6	4	7
BasicTerm.equalsOfPowerList(ArrayList)	10	6	4	7
BasicTerm.equalsOfSinList(ArrayList)	10	6	4	7
BasicTerm.getCosxList()	0	1	1	1
BasicTerm.getPowerList()	0	1	1	1
BasicTerm.getSinxList()	0	1	1	1
BasicTerm.hashCode()	0	1	1	1
BasicTerm.mul(BasicTerm)	0	1	1	1
BasicTerm.mulOfCos(ArrayList)	15	2	6	7
BasicTerm.mulOfPower(ArrayList)	15	2	6	7
BasicTerm.mulOfSin(ArrayList)	15	2	6	7
ConstantNum.ConstantNum(String)	0	1	1	1
ConstantNum.equals(Object)	3	3	2	4
ConstantNum.getBasicTerm()	0	1	1	1
ConstantNum.getNum()	0	1	1	1
ConstantNum.hashCode()	0	1	1	1
ConstantNum.mulOfNegOne()	0	1	1	1
ConstantNum.toString()	0	1	1	1
Cos.Cos(int, Factor)	4	1	4	4
Cos.addPow(int)	0	1	1	1
Cos.equals(Object)	4	3	3	5
Cos.getBasicTerm()	0	1	1	1
Cos.getFactor()	0	1	1	1
Cos.getPow()	0	1	1	1
Cos.hashCode()	0	1	1	1
Cos.toString()	3	3	2	3
DefinedFunc.DefinedFunc()	0	1	1	1
DefinedFunc.addDefinedFunc(String)	1	1	2	2
DefinedFunc.useDefinedFunc(String)	1	1	2	2
Expr.Expr()	0	1	1	1
Expr.addTerm(Term, boolean)	0	1	1	1
Expr.cosPowerIsZero(ArrayList)	3	3	2	3
Expr.equals(Object)	3	3	2	4
Expr.getBasicTerm()	0	1	1	1
Expr.getStrFunc(BasicTerm, BigInteger)	20	3	13	13
Expr.hashCode()	0	1	1	1
Expr.merge()	3	1	3	3
Expr.mergeByPow(int)	7	1	5	5
Expr.powFuncPowerIsZero(ArrayList)	3	3	2	3
Expr.sinPowerIsZero(ArrayList)	3	3	2	3
Expr.toString()	17	1	6	7
Lexer.Lexer(String)	0	1	1	1
Lexer.getDefinedFunc()	5	1	2	4
Lexer.getNum()	2	1	3	3
Lexer.getPowX()	5	1	4	4
Lexer.getSignedNum()	0	1	1	1
Lexer.getSum()	5	1	2	4
Lexer.isCos()	1	1	2	2
Lexer.isDefinedFunc()	1	1	2	2
Lexer.isPow()	1	1	2	2
Lexer.isSignedNum()	1	1	3	3
Lexer.isSin()	1	1	2	2
Lexer.isSum()	1	1	2	2
Lexer.moveBlank()	3	2	2	4
Lexer.next()	12	2	10	11
Lexer.peek()	0	1	1	1
Main.main(String[])	1	1	2	2
Parser.Parser(Lexer)	0	1	1	1
Parser.addDefinedFunc(DefinedFunc)	0	1	1	1
Parser.parseCosFactor()	3	1	3	3
Parser.parseExpr()	8	1	6	6
Parser.parseExprFactor()	3	1	3	3
Parser.parseFactor()	10	8	8	8
Parser.parseSinFactor()	3	1	3	3
Parser.parseTerm()	4	1	4	4
PowFunc.PowFunc(String)	2	1	2	2
PowFunc.addPow(int)	0	1	1	1
PowFunc.equals(Object)	4	3	3	5
PowFunc.getBasicTerm()	0	1	1	1
PowFunc.getPow()	0	1	1	1
PowFunc.getVarType()	0	1	1	1
PowFunc.hashCode()	0	1	1	1
PowFunc.toString()	3	3	2	3
Simplification.simplyPow(HashMap<BasicTerm, BigInteger>)	1	1	2	2
Sin.Sin(int, Factor)	7	1	5	5
Sin.addPow(int)	0	1	1	1
Sin.equals(Object)	4	3	3	5
Sin.getBasicTerm()	0	1	1	1
Sin.getFactor()	0	1	1	1
Sin.getPow()	0	1	1	1
Sin.hashCode()	0	1	1	1
Sin.toString()	3	3	2	3
SumFunc.SumFunc()	0	1	1	1
SumFunc.sumOfFunc(String)	2	2	2	3
Term.Term()	0	1	1	1
Term.addFactor(Factor)	0	1	1	1
Term.cloneMap(HashMap<BasicTerm, BigInteger>)	1	1	2	2
Term.equals(Object)	4	3	3	5
Term.getBasicTerm()	0	1	1	1
Term.hashCode()	0	1	1	1
Term.merge()	14	1	7	7
Term.setNegative(boolean)	0	1	1	1
Total	272.0	151.0	229.0	270.0
Average	2.863157894736842	1.5894736842105264	2.4105263157894736	2.8421052631578947

分析

对比第一次作业的

Total	100.0	45.0	93.0	98.0
Average	2.78	1.25	2.58	2.72

可以看到第二次作业的Iv(G)模块设计复杂度相对于第一次作业有所下降，但基本复杂度和圈复杂度都有所增加。

笔者认为原因在于第二次作业增加了新的因子，Parser和Lexer需要实现对新因子的解析，正是这两个类的对因子的解析造成了复杂度的提高。

类复杂度

Class	OCavg	OCmax	WMC
BasicTerm	3.71	7	52
ConstantNum	1.29	3	9
Cos	1.88	4	15
DefinedFunc	1.67	2	5
Expr	3.5	11	42
Lexer	2.47	11	37
Main	2	2	2
Parser	3.5	8	28
PowFunc	1.62	3	13
Simplification	2	2	2
Sin	2	5	16
SumFunc	2	3	4
Term	2.12	7	17
Total			242.0
Average	2.5473684210526315	5.230769230769231	18.615384615384617

分析

Expr、Lexer、Parser类的复杂度较高。其中Lexer、Parser类的复杂度原因上文已经分析，现在分析一下Expr的复杂度。

在重新看了看代码后，笔者发现笔者在Expr类里实现的toString方法需要判断基本项中的每个列表中的因子指数是否为0，因此与cos、sin、powFunc三个类的耦合较为紧密。

笔者感觉应该可以再新建一个类，专门实现这些基本方法的判断，与Expr类解耦，降低复杂度。

优化策略

由于第二次作业新增了三角因子，因此可以做的优化变得很多。

其中较难实现的是三角函数的平方和cos**2+sin**2=1优化。

笔者也尝试做过平方和的优化，可惜能力有限并未成功，每次在评测机上跑一两百组数据就会出错，于是只能把平方和优化注释掉了。。。但除了平方和以外，能做的小优化还是很多的，除了第一次作业的优化以外，笔者还实现了比如cos(0)=1,sin(0)=0,sin(-1)=sin(1),cos(-1)=cos(1)等优化。

第三次作业

目标

通过对表达式结构进行建模，完成多层嵌套表达式和函数调用的括号展开与化简，进一步体会层次化设计的思想

HW3基本思路

第三次作业可以称得上是OO第一单元最简单的一次作业了。

相比与第二次作业，第三次作业增加的内容有:

1.嵌套括号

2.三角函数因子嵌套

3.自定义函数嵌套调用自定义函数

4.求和函数的求和表达式因子种类增加

可以看出，第三次作业相比与第二次作业其实没有增加什么东西。与前两次作业最大的不同就是第三次作业增加了对嵌套因子，嵌套括号的处理，而这也是笔者觉得第三次作业主要想考察的地方。然鹅，对于递归下降的解析方法来说，处理嵌套因子，嵌套括号本来就是自然而然的事情，因此从第二次作业到第三次作业，笔者几乎不用改动，这也是笔者第一次体会到好的架构设计带来的好处。

当然，几乎不用改动并不是不需要改动。第三次作业由于需要实现自定义函数嵌套调用自定义函数，笔者在第二次作业简单的字符串替换变无法处理了。但解决的办法也很简单，对于自定义函数的调用复用递归下降的办法，对每一个调用因子进行解析，再把解析完成的表达式代入函数表达式中，最后替换完因子后得到一个新的表达式，再对这个表达式进行解析。除此之外，没有需要大改的地方了。

UML类图

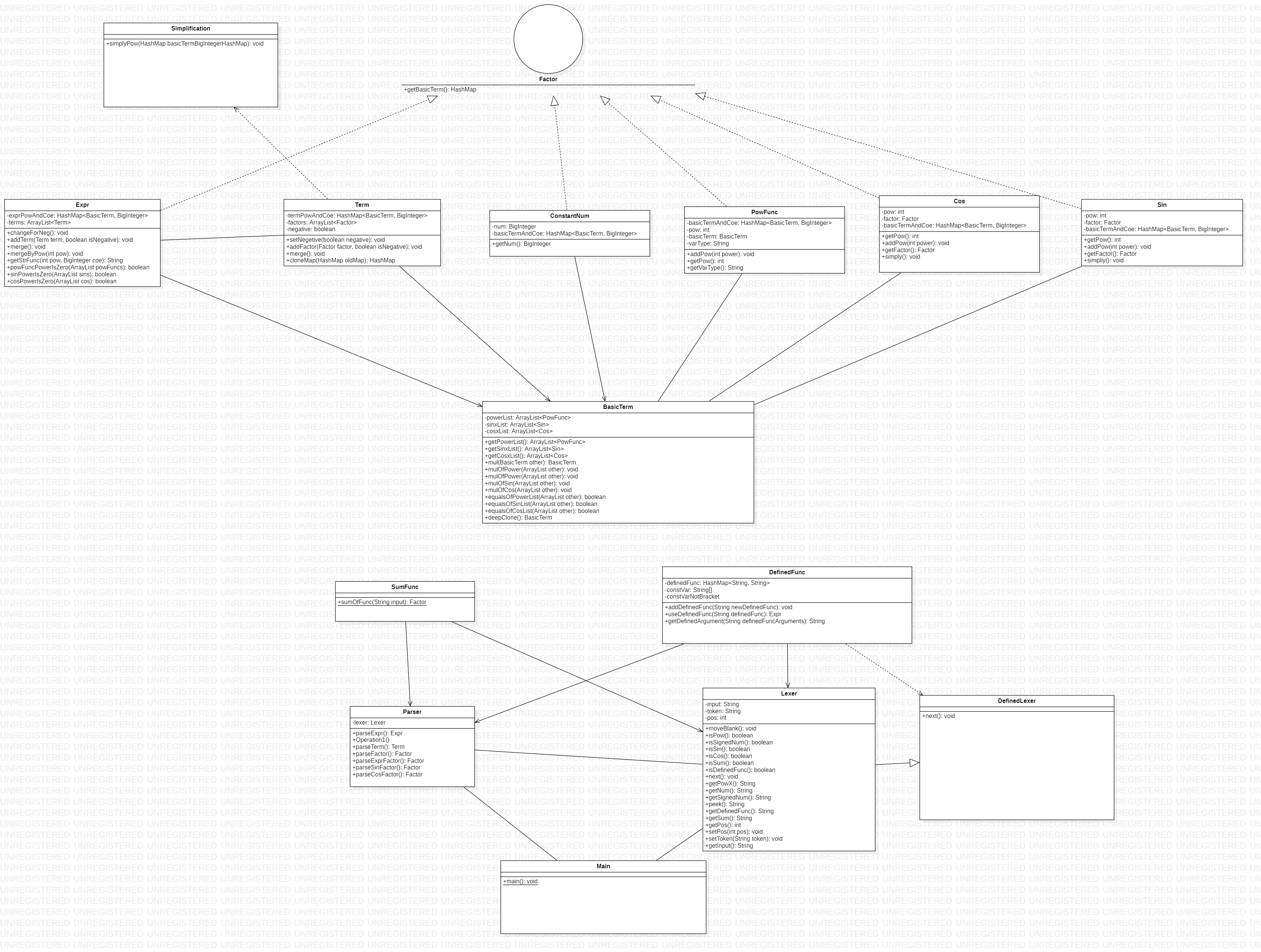
可以看到，第三次作业的UML图与第二次作业的UML图几乎没有变化，新增的DefinedLexer类继承了Lexer类，重写了next方法，实现对自定义函数的文法解析

代码规模

对比于第二次作业的1251行代码，第二次作业总共为1529行代码，主要是增加了DefinedLexer类。其实这次实际的代码只有1287行，为什么呢？因为一大堆失败的优化代码被笔者注释掉了(0.0)

复杂度分析

方法复杂度

Method	CogC	ev(G)	iv(G)	v(G)
BasicTerm.BasicTerm(PowFunc, Cos, Sin)	3	1	4	4
BasicTerm.deepClone()	0	1	1	1
BasicTerm.equals(Object)	4	3	4	6
BasicTerm.equalsOfCosList(ArrayList<Cos>)	10	6	4	7
BasicTerm.equalsOfPowerList(ArrayList<PowFunc>)	10	6	4	7
BasicTerm.equalsOfSinList(ArrayList<Sin>)	10	6	4	7
BasicTerm.getCosxList()	0	1	1	1
BasicTerm.getPowerList()	0	1	1	1
BasicTerm.getSinxList()	0	1	1	1
BasicTerm.hashCode()	0	1	1	1
BasicTerm.mul(BasicTerm)	0	1	1	1
BasicTerm.mulOfCos(ArrayList<Cos>)	15	2	6	7
BasicTerm.mulOfPower(ArrayList<PowFunc>)	15	2	6	7
BasicTerm.mulOfSin(ArrayList<Sin>)	15	2	6	7
ConstantNum.ConstantNum(String)	0	1	1	1
ConstantNum.equals(Object)	3	3	2	4
ConstantNum.getBasicTerm()	0	1	1	1
ConstantNum.getNum()	0	1	1	1
ConstantNum.hashCode()	0	1	1	1
ConstantNum.toString()	1	2	2	2
Cos.Cos(int, Factor)	0	1	1	1
Cos.addPow(int)	0	1	1	1
Cos.equals(Object)	5	3	4	6
Cos.getBasicTerm()	0	1	1	1
Cos.getFactor()	0	1	1	1
Cos.getPow()	0	1	1	1
Cos.hashCode()	0	1	1	1
Cos.simply()	6	2	5	5
Cos.toString()	21	8	13	14
DefinedFunc.DefinedFunc()	0	1	1	1
DefinedFunc.addDefinedFunc(String)	1	1	2	2
DefinedFunc.getBasicTerm()	0	1	1	1
DefinedFunc.getDefinedArgument(String)	1	1	2	2
DefinedFunc.useDefinedFunc(String)	1	1	2	2
DefinedLexer.DefinedLexer(String)	0	1	1	1
DefinedLexer.next()	13	2	11	12
Expr.Expr()	0	1	1	1
Expr.addTerm(Term, boolean)	0	1	1	1
Expr.cosPowerIsZero(ArrayList<Cos>)	3	3	2	3
Expr.equals(Object)	3	3	2	4
Expr.getBasicTerm()	0	1	1	1
Expr.getStrFunc(BasicTerm, BigInteger)	20	3	13	13
Expr.hashCode()	0	1	1	1
Expr.merge()	3	1	3	3
Expr.mergeByPow(int)	7	1	5	5
Expr.powFuncPowerIsZero(ArrayList<PowFunc>)	3	3	2	3
Expr.sinPowerIsZero(ArrayList<Sin>)	3	3	2	3
Expr.toString()	17	1	6	7
Lexer.Lexer(String)	0	1	1	1
Lexer.getDefinedFunc()	5	1	2	4
Lexer.getInput()	0	1	1	1
Lexer.getNum()	2	1	3	3
Lexer.getPos()	0	1	1	1
Lexer.getPowX()	5	1	4	4
Lexer.getSignedNum()	0	1	1	1
Lexer.getSum()	5	1	2	4
Lexer.isCos()	1	1	2	2
Lexer.isDefinedFunc()	1	1	2	2
Lexer.isPow()	1	1	2	2
Lexer.isSignedNum()	1	1	3	3
Lexer.isSin()	1	1	2	2
Lexer.isSum()	1	1	2	2
Lexer.moveBlank()	3	2	2	4
Lexer.next()	12	2	10	11
Lexer.peek()	0	1	1	1
Lexer.setPos(int)	0	1	1	1
Lexer.setToken(String)	0	1	1	1
Main.main(String[])	1	1	2	2
Parser.Parser(Lexer)	0	1	1	1
Parser.addDefinedFunc(DefinedFunc)	0	1	1	1
Parser.parseCosFactor()	3	1	3	3
Parser.parseExpr()	8	1	6	6
Parser.parseExprFactor()	3	1	3	3
Parser.parseFactor()	10	8	8	8
Parser.parseSinFactor()	3	1	3	3
Parser.parseTerm()	4	1	4	4
PowFunc.PowFunc(String)	2	1	2	2
PowFunc.addPow(int)	0	1	1	1
PowFunc.equals(Object)	4	3	3	5
PowFunc.getBasicTerm()	0	1	1	1
PowFunc.getPow()	0	1	1	1
PowFunc.getVarType()	0	1	1	1
PowFunc.hashCode()	0	1	1	1
PowFunc.toString()	6	3	3	4
Simplification.simplyPow(HashMap<BasicTerm, BigInteger>)	1	1	2	2
Sin.Sin(int, Factor)	0	1	1	1
Sin.addPow(int)	0	1	1	1
Sin.equals(Object)	5	3	4	6
Sin.getBasicTerm()	0	1	1	1
Sin.getFactor()	0	1	1	1
Sin.getPow()	0	1	1	1
Sin.hashCode()	0	1	1	1
Sin.simpliy()	14	2	7	7
Sin.toString()	18	6	10	11
SumFunc.SumFunc()	0	1	1	1
SumFunc.getBasicTerm()	0	1	1	1
SumFunc.sumOfFunc(String)	2	2	2	3
Term.Term()	0	1	1	1
Term.addFactor(Factor)	0	1	1	1
Term.cloneMap(HashMap<BasicTerm, BigInteger>)	1	1	2	2
Term.equals(Object)	4	3	3	5
Term.getBasicTerm()	0	1	1	1
Term.hashCode()	0	1	1	1
Term.merge()	14	1	7	7
Term.setNegative(boolean)	0	1	1	1
Total	334.0	173.0	276.0	318.0
Average	3.1809523809523808	1.6476190476190475	2.6285714285714286	3.0285714285714285

分析

这一次作业的复杂度相较于前两次均有所增加，从上表可以看到方法复杂度较高的有Sin.simpliy()，Sin.toString()，Cos.toString()，BasicTerm.equalsOfPowerList(ArrayList<PowFunc>)，Expr.getStrFunc(BasicTerm, BigInteger)，Expr.toString()等。

观察上述方法，可以发现这些方法大多与输出有关，其中cos和sin的toString方法更是iv(G)异常的大。

在重新阅读笔者的代码后，笔者发现这是因为笔者在sin和cos的toString方法中大量使用了if-else来进行输出的化简，比如利用正则表达式匹配x**2，替换成x*x。

现在看来，似乎可以这些化简处理抽象成一个类，专门交给这个类去处理，与cos和sin解耦。

类复杂度

Class	OCavg	OCmax	WMC
BasicTerm	3.71	7	52
ConstantNum	1.5	3	9
Cos	2.78	11	25
DefinedFunc	1.6	2	8
DefinedLexer	6.5	12	13
Expr	3.5	11	42
Lexer	2.16	11	41
Main	2	2	2
Parser	3.5	8	28
PowFunc	1.75	4	14
Simplification	2	2	2
Sin	2.78	9	25
SumFunc	1.67	3	5
Term	2.12	7	17
Total			283.0
Average	2.6952380952380954	6.571428571428571	20.214285714285715

分析

如果你仔细地看了上面的表格，相信聪明的你不难发现有一个类的复杂度特别的大，就是DefinedFunc

DefinedLexer	6.51.6	122	138

这是为什么呢？因为这个类是继承了Lexer类用于解析自定义函数因子，自然需要用到Lexter类中的pos，token等成员变量。

但课程组要求我们每一个类的成员变量应该是private的，连protected都不能用，于是我只能为Lexter类实现了getpos，setpos，gettoken等方法。这看起来似乎不是一个好办法，将Lexer的成员暴露了，Lexter本应该只对外部暴露他的状态。只可惜我没想到太好的办法，只能出此下策。

同时BasicTerm，Expr，Term等类的复杂度也较高，原因在HW2已经阐述，这里就不再赘述了。

优化策略

相比与第二次作业，这次作业支持了三角函数里面添加表达式因子嵌套，因此在此基础上可以做二倍角优化2*cos(x)*sin(x)=sin((2*x)),但经过上一次优化失败的教训后笔者也不敢再优化了，实在是太容易出bug了，于是也没做二倍角优化。这次作业的优化和HW2相同。

听说有人做了二倍角和平方和优化，并通过比较不同优化的长度，搜索到最长的输出，如果超时就及时熔断。但笔者觉得除非特别厉害，否则这样就是在刀尖上起舞(事实证明的确是这样，详见下文)。

整体架构分析

从第一次作业到第三次作业，我的程序紧紧围绕着一个基本项展开，在第一次作业中他是保存有指数和系数的HashMap<Integer, BigInteger>；第二、三次作业中，他是一个类BasicTerm。但这样的设计我觉得并不好，因为并不利于迭代开发。一个基本项显然只能涵盖较为简单的情况，比如三角函数、幂函数这样的，一旦表达式中的函数因子多了起来，这个基本项也会变得极为庞大和复杂，显然与OO的精神违背。

同时我的化简运算merge()也是各自在term类和Expr类中实现的，term中是乘，Expr中是加。这样我也感觉并不好，因为term现在只有乘的运算，但如果有取模和除法运算呢？想必我就要修改原来的term类了。而这种运算并不是term类应该具有的能力，这种运算应该交给“运算类”专门去做，而不是在term类中实现。

现在想来，一个好的设计应该是表达式中每一种因子，每一种运算，每一项，都应该成为一个类，即使需求变了，也只需要增添新的运算类和因子类即可，无需或者很少需要改动原来已经设计好的代码。

数据生成及自动化评测

在OO第一单元的每次作业中，笔者都使用Python及其xeger库写了数据生成器，并在第二次作业和第三次作业实现了自动化评测机

第一次作业

数据生成

根据指导书中的设定的形式化表述

• 表达式 → 空白项 [加减 空白项] 项 空白项 | 表达式 加减 空白项 项 空白项
• 项 → [加减 空白项] 因子 | 项 空白项 * 空白项 因子
• 因子 → 变量因子 | 常数因子 | 表达式因子
• 变量因子 → 幂函数
• 常数因子 → 带符号的整数

我们可以自底向上构造测试用例，首先构造因子中的变量因子和常数因子，通过这两个因子构造没有表达式因子的项，再通过没有表达式因子的项，构造没有括号的表达式，通过把没有括号的表达式加上括号，我们就得到了表达式因子，再用三种因子构造含有表达式因子的项，最后用含有表达式因子的项生成表达式

其中，变量因子和常数因子的构造可以使用Python的xeger库（根据正则表达式随机生成字符串）

再通过调节不同因子的生成概率和程度，可以得到不同强度的数据

缺点:对于边界数据难以生成，可以考虑添加边界数据常量池，在生成表达式时随机添加

代码示例

展开代码

from xeger import Xeger
import random

powFun = 'x( ){0}(\*\*( ){0}\+0{0}[0-4])?'
const = '(\+|-)0{0}[1-9]{1}'

x = Xeger(limit=100)
x._cases['any'] = lambda x: '.'
x._alphabets['whitespace'] = ' '

def generTermNotExp(x,notpre):



def generExpNotBrac(x,notpre):


def generTermWithBracket(x, notpre):


def generExpWithBracket(x):


for i in range(100):
    s = generExpWithBracket(x)
    print(s)

自动化评测

本次作业未实现自动化评测🤡

第二次作业

数据生成

本次数据生成器根据第一次作业的数据生成器迭代开发，大体上思路不变。根据第二次作业的指导书新增的三角因子，自定义函数，求和函数的因子生成，其中自定义函数参考了讨论区大佬的方法。

缺点:同作业一一样，对于边界数据难以生成，可以考虑添加边界数据常量池，在生成表达式时随机添加

代码示例

展开代码

from xeger import Xeger
import random

#powFun = 'x( ){0}(\*\*( ){0}\+0{0}[0-4])?'
powFun = 'x'
const = '(\+|-)0{0}[1-9]{1}'
power = '( ){0}(\*\*( ){0}\+0{0}[0-4])?'
# fun1,fun2,fun3分别是函数参数为1个，2个，3个的函数，而且函数名分别为f，g，h
list_fun1 = ["f(x)=x", "f(y)=sin(y)", "f(z)=z*z", "f(y)=y*y"]
list_fun2 = ["g(x,y)=x+y", "g(y,z)=sin(y)*cos(z)", "g(x,z)=x*z+x-z", "g(z,y)=y*y-z+2"]
list_fun3 = ["h(x,y,z)=x+y-z", "h(x,z,y)=sin(x)+y+cos(z)", "h(x,z,y)=x+y*(z-1)", "h(x,y,z)=y*y*x*(4-z)"]
list_fun = [list_fun1, list_fun2, list_fun3]

# 用于替换函数参数的变量，即若函数为f(y)=sin(y)，则从list_var中随机一个当作y填入函数
list_var = ["1", "2", "x", "x**2", "x**3", "x**0"]

fun_java = []  # 随机出了哪些函数，记录一下，java输入时要用到
fun_record = []  # 函数名不能重复，也记录一下
x = Xeger(limit=100)
x._cases['any'] = lambda x: '.'
x._alphabets['whitespace'] = ' '

def generate_function():


def generSin(x):



def generCos(x):


def generSum(x):


def generExpFactorNotDefinedFuncAndSum(x,notpre):


def generTermNotExpDefinedFuncAndSum(x, notpre):


def generTermNotExp(x, notpre):



def generExpNotBrac(x, notpre):


def generTermWithBracket(x, notpre):



def generExpWithBracket(x):

print(0)
s = generExpWithBracket(x)
print(s)

自动化评测

在看了cnx大佬的评测思路和讨论区的评测思路后，基于cnx大佬的代码实现了一个简易的评测机。

利用Python的subprocess库进行java程序的输入输出，利用eval函数对java程序的输出进行代值运算，如果有错误，就将输入数据和输出结果输入到文件中

评测机输入从数据生成器获得

代码示例

展开代码

import subprocess
from math import *
import os
import data


def getinput():
    s = data.generdata()
    while len(s) > 200:
        s = data.generdata()
    return s

# 其中cmd代表IDEA运行时的控制台最上面的那一串路径
cmd_my = r''

cmd2 = r''

cmd3 = r''

cmd4 = r''

cmd6 = r''

cmd7 = r''

cmd8 = r''

testcmd2 = cmd2
testcmd3 = cmd3
testcmd4 = cmd4
testcmd5 = cmd5
testcmd6 = cmd6
testcmd7 = cmd7
testcmd8 = cmd8
for i in range(60000):
    java_input = getinput()
    print("----input----")
    print(java_input)
    print("-----------")

    proc = subprocess.Popen(cmd_my, stdin=subprocess.PIPE, stdout=subprocess.PIPE, stderr=subprocess.STDOUT,
                            encoding='gb2312')
    stdout, stderr = proc.communicate(java_input)
    out1 = stdout.split("\n")[1]
    print(out1)
#省略一部分

第三次作业

数据生成

第三次作业数据生成思路与第二次作业大体上相同，但是第三次作业支持三角因子内嵌套任意因子，以及括号嵌套，同时sum表达式里不能有自定义函数和求和函数。

因此将三角函数因子分为有求和函数、自定义函数，和没有求和函数自定义函数、求和函数两种，sum因子生成时如果要用到三角函数则采用后者。

通过递归生成每一项时对项、因子、表达式添加括号生成嵌套括号。

自定义函数的递归调用通过常量池的方式手动添加。

代码示例

展开代码

from xeger import Xeger
import random

# powFun = 'x( ){0}(\*\*( ){0}\+0{0}[0-4])?'
powFun = 'x'
const = '(\+|-)0{0}[0-9]{1}'
power = '( ){0}(\*\*( ){0}\+0{0,1}[2-3])?'

# fun1,fun2,fun3分别是函数参数为1个，2个，3个的函数，而且函数名分别为f，g，h
list_fun1 = ["f(x)=x", "f(y)=sin(y)", "f(z)=z*z", "f(y)=y*y", "f(z)=sin(cos(z))"]
list_fun2 = ["g(x,y)=x+y", "g(y,z)=sin(y)*cos(z)", "g(x,z)=x*z+x-z", "g(z,y)=y*y-z+2", "g(z,x)=cos((z*x))"]
list_fun3 = ["h(x,y,z)=x+y-z", "h(x,z,y)=sin(x)+y+cos(z)", "h(x,z,y)=x+y*(z-1)", "h(x,y,z)=y*y*x*(4-z)",
             "h(z,x,y)=sin(x)*y+x"]
list_fun = [list_fun1, list_fun2, list_fun3]

# 用于替换函数参数的变量，即若函数为f(y)=sin(y)，则从list_var中随机一个当作y填入函数
list_var = ["1", "2", "x", "x**2", "x**0", "f(g(x**1,cos(x)))", "g(f(0),g(x,1))", "h(1,1,1)", "0", "cos(-0)", "sin(-0)",
            "sum(i, -2, 1, i*cos(x))","sin(sin(sin(0)))","cos(sin(0))","cos(cos(0))","sum(i, 0, 2, i)","g(h(sum(i,-2,-1, i), f(cos(sin(x**1))),sum(i,2,2,(i*cos(i))) ),sum(i,-2,2,sin(i)) )"]

fun_java = []  # 随机出了哪些函数，记录一下，java输入时要用到
fun_record = []  # 函数名不能重复，也记录一下

x = Xeger(limit=100)
x._cases['any'] = lambda x: '.'
x._alphabets['whitespace'] = ' '


def generate_function():


def generSin(x):


def generCos(x):


def generSinNotSumAndDefined(x):


def generCosNotSumAndDefined(x):


def generSum(x):

def generExpFactorNotDefinedFuncAndSum(x, notpre):


def generTermNotExpDefinedFuncAndSum(x, notpre):


def gengerFactor(x):


def generFactorNotSumAndDefined(x):


def generTermNotExp(x, notpre):


def generExpNotBrac(x, notpre):


def generTermWithBracket(x, notpre):


def generExpWithBracket(x):



def generdata():
    global x
    s = "0\n" + generExpWithBracket(x)
    return s

自动化评测

本次测评机与HW2相同，故不再赘述

自我程序bug分析及测试手段

自我程序bug分析

第一次作业

在写完代码进行自我测试时主要的bug是lexer解析的问题，忽略了一些符号的优先级

本次作业强测和互测都未被找出bug

第二次作业

这次作业的bug令我☹️

bug出在化简，将cos(0)化成了0，出现这个bug的原因是因为cos的化简代码是我从sin那复制过来的，而sin(0)=0，忘记改了🤒

导致强测WA3个点，互测被hack一次

痛，太痛了

这也再一次提醒了我，永远不要复制代码！！！！！！！！！！

第三次作业

本次作业强测和互测均未被找出bug

测试手段

第一次作业

由于未编写评测机，故只能手工进行对拍。

步骤:

1.将程序输入改为循环

2.从数据生成器复制输出的数据

3.将数据输入自己的程序

4.将数据输入到他人程序

5.将他人程序输出输入到自己程序

6.使用文本差异比较器对比第3步和第4步的输出

可以看出，没有评测机下想要对拍是极为困难且麻烦的，这也坚定了当时我要搭建评测机的决心

第二次作业

搭建了评测姬以后第二次作业测试较为顺利，只需要利用评测机和数据生成器自动化评测即可。笔者利用评测机帮助同学测出了几个bug，十分有成就感。

但是，由于一系列历史原因，笔者的数据生成器竟然忽略了0的生成，导致无法生成cos(0)这样的数据，也是笔者第二次作业翻车的根本原因。同时也说明了不能过度依赖评测机，还是有必要重复阅读自己的代码的。

第三次作业

和第二次作业测试过程基本相同，同样也帮助几位同学找出了程序的bug，成就感满满~

他人程序bug分析

第一次作业

本次作业找到同房间两个bug

1.第一个人的bug是-1会只输出个-号

2.第二个人的bug是5161*x会输出516*x,推测是正则表达式出的锅

第二次作业

本次作业找到同房间4个bug

1.第一个bug是-cos(2)*cos(x)-cos(x)会输出-2*cos(x)，推测是三角函数相乘没有处理好

2.第二个bug是sin(-1111111111111111111111)会爆int,看了代码以后发现这位同学hashcode使用了parseInt来解析BigInter

3.第三个bug是(cos(x)**2+sin(x)**2)**2会输出cos(x)**3+cos(x)**2*sin(x)+sin(x)**2*cos(x)+sin(x)**3，原因应该是平方和优化出了问题，这也说明一定要在保证正确性的基础上进行优化

4.第四个bug是x**11输出x，推测是这位同学没有仔细阅读指导书，x**10以上的指数没有处理

第三次作业

本次作业找到同房间7个bug

1.第一个bug是sin((-x))**2输出sin(-x)**2，推测是没有处理好三角函数内因子的输出，导致WF

2.第二个bug是+3+-cos(sum(i,2,1,0))**+2会输出4，推测是平方和和二倍角优化出现的问题，这再一次提醒我们，一定要在保证正确性的基础上进行优化。在这里，不得不提一下，这位同学的优化出现了相当多的问题，导致我hack了三次以后就不敢再hack了。测评机每跑十几条数据就会WA，但这样仍能进入A房，由此可见强测的数据不一定强。

3.第三个bug是cos(sin(cos(sin(cos(sin(cos(sin(cos(x)))))))))，有第二个bug的同学的程序在输入这条数据后会直接TLE，可能是优化做得太狠，并且没有及时熔断。

4.第四个bug是-sin(x)**+2+-sin(x)*cos(x)**+2++cos(x)*x会输出x*cos(x)-sin(x),推测也是三角函数乘三角函数合并时没有处理好

5.第五个bug是sum(i,0,0,(-i+cos(sin(sin(-9)))*cos(i)-cos(-5)))会输出cos((0))*cos(sin(sin((-9))))0-cos((-5)),可以发现中间输出多了个0，看了代码以后发现应该是sum处理时候出现的问题

6.第六个bug是sum(i,-1,1,i**2)会输出0，观察代码后发现是没有处理好i作为幂函数自变量的情况

7.第七个bug是sum(i,123456789123456780,123456789123456789,i)，观察代码后发现是sum的上下界使用了int存储，因此遇到大数据会爆int。同时发现有些人上下界是拿long存的，可惜课程组互测限制太死，无法构造出爆long的数据

hack别人程序bug策略

第一次作业

由于未编写评测机，故只能根据数据生成器采用测试手段中第一次作业的测试方法，手动构造了一些边界数据。成功hack到两个人。

第二次作业

由于搭建了评测机，我的策略是查看他人代码，看看有没有地方会爆int什么的，然后先手动输入一些可能有bug的边界数据，测试完边界数据以后交给评测机自动化评测(高工能留给OO的时间真的不多)，然后去干别的事情(实现并行)，隔一段时间看看文件是否有WA输出

第三次作业

hack方法同第二次作业

hack策略分析

虽然通过阅读他人代码+评测机随机轰炸能覆盖到绝大多数点，但仍有一些边界数据是难以被构造出来的，并且评测机生成的数据有时过于复杂，不利于hack输入的提交，简而言之，就是难以构造强而简单的数据。

这样会导致虽然跑了很多组数据，但是仍有bug的情况发生。可以说，评测机只是帮助测试的一种手段，并不能完全覆盖所有情况，不能严格证明代码的正确性。

心得体会

在OO第一单元的学习中，我有如下几个体会和收获

• 初步学习了递归下降算法并运用在表达式解析中，再一次领略到了递归的美妙
• 通过阅读字数颇多且没有废话的指导书，我提升了快速从一份篇幅较长的资料中获取有用信息及需求的能力
• 通过指导书，接触到了形式化语言
• 第一次利用python的xeger和subprocess模块写出了属于自己的数据生成器和评测姬，实现了上学期计组没有实现的梦想
• 学会了使用IDEA及其插件，并利用checkstyle使代码风格变得更好
• 了解到了黑盒测试、白盒测试、回归测试等测试方法
• 体会到了好的架构的重要性
• 理解到了重构的必要性和学会了应该如何进行重构
• 认识了许多6系的同学，收获了跨院系的友谊

从作业难度上来看，我认为第一次作业≈第二次作业>>第三次作业，因为第一次作业是从无到有的过程，需要学习递归下降算法且完整地把代码写出来。而第二次作业虽然有了第一次作业的架构，但因为第一次作业的架构有部分不适合第二次作业，因此需要进行重构，因此也有一定难度。而第三次作业就是福利大放送了。

从面向对象的思维来看，虽然在设计过程中我努力地让自己“面向对象”，可是写出来的代码还是处处“面向过程”。面向对象是一种思维，但有了这种思维将其实现还是有一定难度的，更不要说我还没有这种思维。

而且设计模式我也不了解多少，只知道装饰者模式、观察者模式、策略模式、工厂模式啥的，而且这些模式也是我开学以后抽空看的，想在作业中运用这些模式的时候架构已经成型，不敢随便乱改了，令人有点遗憾。因此我建议课程组可以在pre的时候提供给同学们一些资料或者书籍，帮助同学们了解一些设计模式，以便在第一单元更好地运用。虽然设计模式不是看了就会的，但我觉得看了心里有个谱，起码比啥都不了解就开始写面向对象的代码还是要强一点的。

鸣谢

感谢wzm同学和我讨论架构，以及分享测试数据

感谢cnx提供的评测机思路

感谢为我提供程序进行对拍的同学