CSP-S T3函数调用
函数是各种编程语言中一项重要的概念,借助函数,我们总可以将复杂的任务分解成一个个相对简单的子任务,直到细化为十分简单的基础操作,从而使代码的组织更加严密、更加有条理。然而,过多的函数调用也会导致额外的开销,影响程序的运行效率。
某数据库应用程序提供了若干函数用以维护数据。已知这些函数的功能可分为三类:
- 将数据中的指定元素加上一个值;
- 将数据中的每一个元素乘以一个相同值;
- 依次执行若干次函数调用,保证不会出现递归(即不会直接或间接地调用本身)。
在使用该数据库应用时,用户可一次性输入要调用的函数序列(一个函数可能被调用多次),在依次执行完序列中的函数后,系统中的数据被加以更新。某一天,小 A 在应用该数据库程序处理数据时遇到了困难:由于频繁而低效的函数调用,系统在执行操作时进入了无响应的状态,他只好强制结束了数据库程序。为了计算出正确数据,小 A 查阅了软件的文档,了解到每个函数的具体功能信息,现在他想请你根据这些信息帮他计算出更新后的数据应该是多少。
输入格式
第一行一个正整数 n,表示数据的个数。
第二行 n个整数,第 i个整数表示下标为 i的数据的初始值为 ai。
第三行一个正整数 m,表示数据库应用程序提供的函数个数。函数从 1∼m编号。
接下来 m行中,第 j(1≤j≤m)行的第一个整数为 Tj,表示 j号函数的类型:
- 若 Tj=1,接下来两个整数 Pj,Vj分别表示要执行加法的元素的下标及其增加的值;
- 若 Tj=2,接下来一个整数 Vj 表示所有元素所乘的值;
- 若 Tj=3,接下来一个正整数 Cj表示 j号函数要调用的函数个数,
随后 Cj个整数 g1(j),g2(j),…,gCj(j)依次表示其所调用的函数的编号。
第 m+4 行一个正整数 Q,表示输入的函数操作序列长度。
第 m+5行 QQ 个整数 fi,第 i个整数表示第 i个执行的函数的编号。
输出格式
一行 n个用空格隔开的整数,按照下标 1∼n的顺序,分别输出在执行完输入的函数序列后,数据库中每一个元素的值。答案对 998244353 取模。
题解:
这个题,研究之后发现真的是好题;
首先题目中的调用关系提示我们应该是个有向图,同时,函数不会直接或者间接的调用自己,所以不会出现环的情况
有向图上的算法有哪些呢?拓扑排序,最后的q次调用函数,也可以写成等同于m次操作,只是他为0号,会调用q次函数,所以以0号为超级原点,建立有向图即可
题目中提示了,如果只有操作1或者只有操作2怎么办?
如果只有乘法操作,哎呀,爽歪歪,直接拓扑排序,记录最终0号节点被乘了多少次x就行了,最终序列中所有的值直接乘以x即可
如果只有加法操作呢?暂时不会
加法操作和乘法操作混在一起的时候,就比较难计算,因为加法操作会被乘法操作影响,但是,我们考虑,加法操作会被哪些乘法影响呢?他只会被自己后面进行的乘法影响,所以对于每一个加,我们是否可以计算出这个加法操作被乘法执行了多少次,执行了多少次就是加法的倍数,最后我们用被加数*倍数就可以得到加的值是多少,以下图举例:
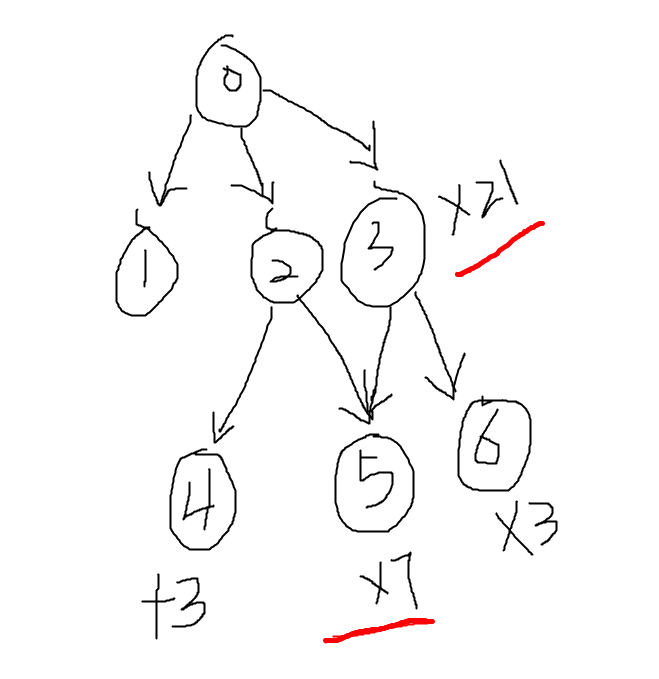
例如图中的+3操作,会被后面的*5影响,同时也会被3操作影响,当我们第一遍拓扑排序的时候,已经把每个节点的乘处理出来了,现在我们考虑怎么把+3被执行了多少次?
+3会被自己子树内的后面的乘法影响,同时还会被父亲节点后面的乘法节点影响,怎么计算呢?计cnt[v]表示v这个加法后面有多少乘法?如何递推呢?cnt[v]=cnt[v]+cnt[u]*cm,cm表示子树内目前被执行了多少次,cnt[u]表示父亲后面有多少乘法,cnt[u]*cm表示目前有多少乘法。当然,cnt[0]=1,这一点千万别忘了,如果这个值为0的话,只能计算子树内的贡献了
问题一:在做的过程中,有一个问题值得注意,既然0号节点连接其他节点,那么我们直接把0号节点放入队列中即可,为什么还需要枚举0-m呢?
因为在建图的过程中,有些节点虽然没有被0号节点调用,但是可能和最终节点连接,如果我们只把0号节点push进队列中,那么子节点有可能不能变成入度为0的点,就会有错误,换句话说,因为我们在建图的过程中,把所有点都放在图中了,但是在最终调用的时候却没有把某些点放在图中拓扑,所以会出现错误。
问题二;把没有被0号节点调用的点放入第二次拓扑中,会不会对答案产生影响呢?如下图
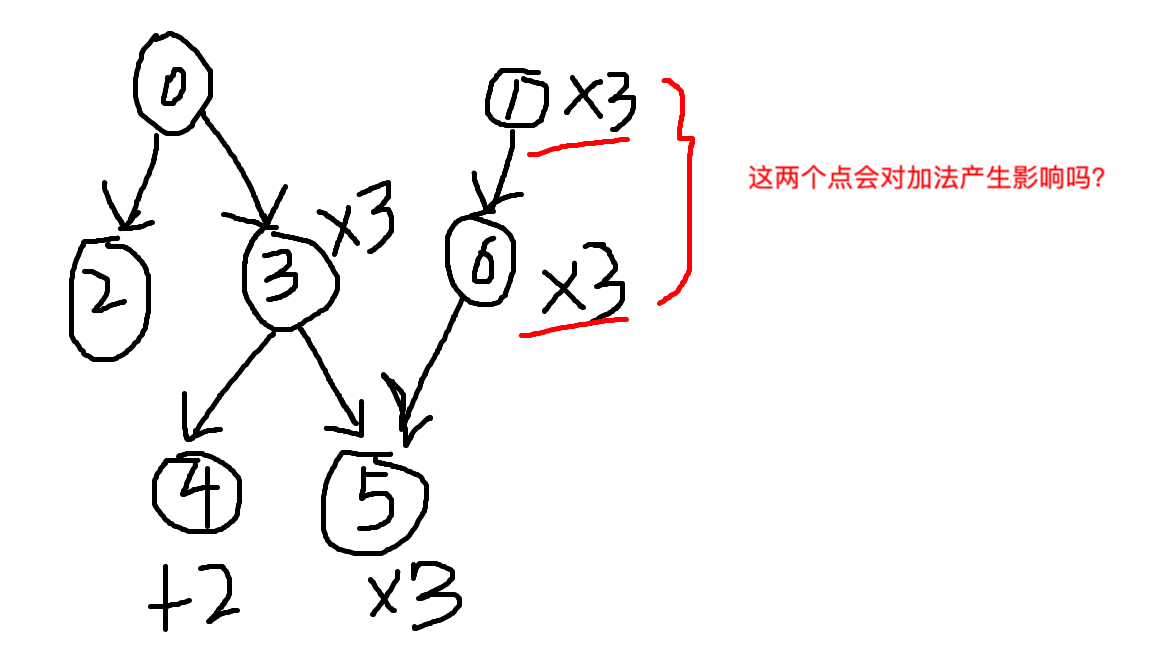
答案是不会,因为虽然乘法上会产生影响,但是我们只设定了cnt[0]=1,其他入度为0的点cnt[]的值均为0,所以根本更新不到子树



