[BZOJ4403]序列统计

有个套路：计算单调不降的，可以给第i项加一个i，转化成单调递增的，然后就变成了在值域[L+1,R+N]中取1~n个数。

复制一下popoqqq大佬的图片

M=R-L+1。

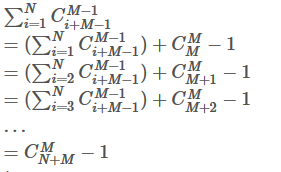
式子就变成了这个样子。

Lucas定理随便做了。

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int mod=1e6+3;
int n,l,r,T;long long fac[mod+5],inv[mod+5];
long long solve(long long x,long long y) {
    if(y<x) return 0;
    if(x<mod&&y<mod) {return (fac[y]*inv[x]%mod)*inv[y-x]%mod;}
    return solve(x%mod,y%mod)*solve(x/mod,y/mod)%mod;
}
long long ksm(long long d,int z) {
    long long res=1;
    while(z) {
        if(z&1) res=res*d%mod;
        d=d*d%mod;
        z>>=1;
    }
    return res;
}
int main() {
    scanf("%d",&T);
    fac[1]=fac[0]=1;
    for(long long i=2;i<=mod;i++) fac[i]=(fac[i-1]*i)%mod;
    inv[mod-1]=ksm(fac[mod-1],mod-2);
    for(long long i=mod-2;i;i--) inv[i]=(inv[i+1]*(i+1)%mod);
    inv[0]=1;
    while(T--) {
        scanf("%d%d%d",&n,&l,&r);
        printf("%d\n",(solve(r-l+1,r+n-l+1)-1+mod)%mod);
    }
}