贴现因子

 

贴现因子(discount factor)，也称折现系数、折现参数、折现因子

是贴现因子

　　所谓贴现因子，就是将来的现金流量折算成现值的介于0－1之间的一个数。

　　一般来说，当利率为r时，承诺T年之后支付R美元的现值是R美元／(1+r)T。因此，即使没有通货膨胀，将来1美元的价值也小于现在1美元的价值，必须按某一数额贴现，该数额取决于利率的高低和收到货币的时间长短。其中1/ (1+r) T被称为未来T时期的货币的贴现因子(discount factor)。

　　贴现因子δ=1/(1+r)，0<δ<1,r是贴现率。贴现值为1/(1-δ)

 

现值与贴现因子

　　在计算现值时，贴现因子起着很重要的作用:

 

单利贴现因子

　　

[编辑]

复利贴现因子

　　

[编辑]

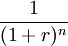
连续复利折现因子

　　

 

贴现因子的几种定义和理解

　　贴现因子在数值上可以理解为贴现率，就是1个份额经过一段时间后所等同的现在份额。这个贴现因子不同于金融学或者财务学的贴现率之处在于，它是由参与人的“耐心”程度所决定的。“耐心”实质上是讲参与人的心理和经济承受能力，不同的参与人在谈判中的心理承受能力可能各不相同，心理承受能力强的可能最终会获得更多的便宜；同样，如果有比其他参与人更强的经济承受能力，也会占得更多的便宜。

　　学者在博弈论对贴现因子的定义：

　　贴现因子是讨价还价博弈中的一个很重要的概念，Gibbons将贴现因子定义为“货币的时间价值”，实际上就是贴现率＝1/1＋r；

　　张维迎的博弈论中将贴现因子解释为参与人的耐心程度，贴现因子表示一个参与人的耐心程度，取值在『0，1』，越大说明参与人的耐心越好，若是等于0则说明参与人完全没有耐心。由于贴现因子是由公式 1/1＋r定义的，那么可以看到，收益率越大，则贴现因子越小，则参与人的耐心程度越小；反之，如果收益率越小，则贴现因子越大，参与人越有耐心。

 

关于贴现因子的讨论

　　行为经济学的研究目前越来越受到人们的重视，特别是今年诺贝尔经济学奖授予了研究实验经济学和行为经济学的经济学家以后。行为经济学的研究就是在考虑人们的决策过程中要注重人们的行为对决策的影响，如在分析资产定价理论时，Caplin 和Leahy(2001)考虑了人们对风险的紧张程度来考虑资产定价行为， Barberis, Huang和Santos(2001)考虑人们的预期行为对资产定价的影响，Abel (1990), Constantinides (1990), Sunderason (1989)和Campbell和Cochrane (1999)引入“习惯资本”形成对资产定价的影响；在考虑经济增长时，Kurz（1968），Zou（1994，1996）引入人们对社会地位的追求来讨论这种追求对经济增长的影响；Carroll 和Samwick(1997)和Carroll，Overland 和Weil (2000) 讨论“习惯资本”对经济增长的影响等等，诸如此类的模型都考虑了人们行为对经济决策的影响。实际上，在经济学中，人们已经早就注意到了个体行为对经济的影响，如我们通常所讲的效用函数就是基于人们对商品的偏好形成的，同时在研究人们的决策过程中，考虑人们的跨时决策行为时不可避免地要涉及到人们对将来的耐心程度，这就是经济学中经常提到的贴现因子。

　　关于贴现因子的讨论必须要追溯到人们对跨时选择问题的研究。关于人们对跨时选择的讨论可以追溯到Adam Smith的著作“《国富论》”，但是，是苏格兰经济学家John Rae 最早考虑了人们在跨时选择过程中的社会行为和心理行为，提出了跨时选择的必要条件，但是，所有的这些讨论，直到1937年Samuelson 给出了贴现效用模型才使得经济学家对跨时选择的研究有了理论基础，虽然Samuelson 给出的贴现效用模型很简单，也具有较大的局限性，但是这个模型一经给出就立即被人们接受，而且被广泛地引用，这主要是因为它不仅是公共跨时选择的理论基础，也是对人们实际行为的较好描述。贴现效用模型的重要假设就是人们在不同时间获得的效用可以用一个简单因子来区分，这个因子就是贴现因子，它表示了人们对将来的耐心程度。为简单起见，Samuelson把它看成是一个常数，也就是说人们在今天对明天，和人们处于明天对后天的耐心程度是一致的。这个假设当然具有很大的局限性，在Samuelson以后的经济学家对贴现因子作了很多重大的改进。主要有：Uzawa (1968) 给出的内生贴现因子模型，Becker和Mulligan(1997)提出贴现因子模型，Laibson(1997，2001)给出了双曲贴现因子模型，Marshall的贴现因子模型，Takashi Kamihigashi(2002)给出的非线性贴现因子模型和Gong和Zou的贴现因子模型(2002)。a