卷积码
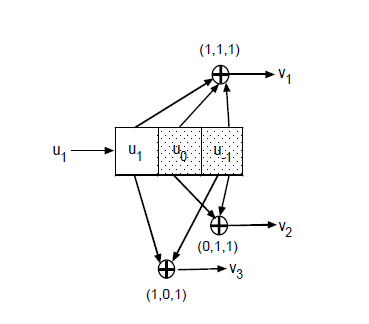
刚学习卷积码的时候,望文生义的理解方式:用卷积的方式实现信道编码。问题是如何实现?翻阅了很多papers之后,介绍卷积码的编码实现过程使用的是零散的模块(移位寄存器、mod2加法器、生成多项式)的功能和特点,通过mod2和实现编码的输出,这个过程类似卷积(生成多项式和输入比特的卷积)。但是,这种思考方式,仅仅将模块连接,并未深入研究,模块的本质内容是什么?在老师不断的“头脑风暴”下,慢慢发现,移位寄存器存储的是一个个状态组合,而这个状态组合的个数与约束度(constraint length)有关;mod2加法器使编码输出比特不仅仅与当前输入信息有关还有之前的若干blocks里的编码信息有关;而生成多项式决定的则是block的选择(选择不同,编码输出不同,编码效果体现在接收端误码率)。这样,输入编码是状态变化的原因,编码输出是状态变化的结果。整个系统就围绕着“状态”进行不断的编码,而“状态”不断变化、循环直到编码完成。
这样,编码过程就可以应用一个经典的“状态机模型”,而状态机模型的不同表达方式也使得整个编码过程在时间和空间两个维度展现出来。例如,状态图,即是一个很好的表示状态变化的图形。但是由于循环反复的利用状态信息,但在时间上,并未很好的体现卷积码的编码过程。相比,树形图,在时间上进行延展,很直观的表现出状态变化的过程,但是状态信息未重复利用,使得存储空间大小得到限制(指数增加)。最后,网格图很好的展现了时间和空间两个维度信息,很适合分析卷积码的编码过程。而用Matlab实现卷积码编码的时候,我按照传统卷积码编码方法(只考虑实现,未考虑算法的优化),中规中矩的编码思路,但在速度上,并未得到很好的保证。而老师给的编程思想则是:给出每个以为寄存器中随时间变化存储的二进制信息。例如,4个移位寄存器,则每个移位寄存器存储的信息分别为:[abcdefg000;0abcdefg00;00abcdefg0;000abcdefg],所以矩阵的纵列信息即为所有寄存器中瞬时状态信息,而生成多项式中数值为‘1’的移位寄存器存储比特信息将参与mod2运算。这样利用矩阵的乘法直接完成查找移位寄存器中对应生成多项式数值为‘1’位置的信息。相比我的编码思路(循环查找寄存器里对应生成多项式数值为‘1’的信息),运算速度大大提升。同时,在对状态机模型的认识也进一步深入,即,编码过程为移位寄存器中状态不断变化的过程。(编码用‘状态’描述,并且将‘状态’融入到算法实现中)
在完成解码的过程中,找了许多关于Viterbi算法的papers,但在编码过程对状态机模型的认识过程中,意识到,解码过程对状态机模型的依赖。实际上,Viterbi算法就是一个在状态机模型基础上不断减少可能路径的一个过程。因为解码是编码的一个逆序过程,接受比特和初始状态是我们已知的信息,我们无法找到一个逆序的算法来计算输入比特信息。所以Viterbi算法利用的就是‘重新编码’的思想,计算每条路径可能的概率值大小,用概率最大的路径来模拟编码过程。从而得到输入比特信息。而状态机模型的应用大大提升了解码过程寻找正确路径的速度。而在用matlab算法实现的过程中,老师用initial state和next state作为矩阵的行列号,查找输入比特的速度比我实现时不断循环查找状态表提升很多,也使最后所画的误码率对比图达到理想的接受比特个数(提高了系统的运算能力)。还记得答辩时候老师问我的那个问题:如果接受比特中错误比特的数量一定(假设都是10个),那么错误比特均匀分布和集中分布两种方式哪个误码率性能比较好?听到问题的时候,脑袋想过的编码过程,错误比特的分布情况,所以回答的一塌糊涂。后来才在老师的解释下,明白了题目的意思。老师想问的是,错误比特(信道噪声影响)的排列分布对解码时误码率性能的影响。卷积码编码的时候就假设,每个block是相对独立的,而瞬时编码的时候,输出比特不仅仅与当前的输入比特信息有关,还与之前的若干blocks里的信息有关(联合概率)。所以在解码的时候,每组接收比特的信息也与之前的若干比特信息是相关联的。所以,如果误码比较集中,在Viterbi时,权值的计算时就会相对增加权值的比重(大的越大,小的越小),容易将该条路径淘汰。而误码分散排列时,一些权值有可能比较接近,无法淘汰。因此误码集中分布的情况,系统的误码率性能较好。老师的问题,一定程度上又深化了我对整个系统认识的深度。不仅仅在编码上,而且在解码端理解卷积码的意义:用相邻信息编码、解码,使得信息能在信道中准确传输。
而抛开状态机模型的应用,Viterbi算法的关键在于路径选择的权值(metric)问题.权值的计算的优化能大大提升系统误码率的大小。这样,就到了最后一个问题,硬判决和软判决对系统误码率的提升能力分析。从星座图的角度看,误码率性能体现在是否能够找到正确的接收比特组合信息,即纠正错码的距离(纠正错码的能力)。硬判决在解调时直接将接受比特映射到‘0’,‘1’的星座图空间上,那么使用汉明距离(100%的概率决定接收比特信息)就可以将接收比特投射到相应的星座图位置,这样,如果产生错码,硬判决解码的纠正错码的距离将很大(正方形的边长或对角线)。而软判决解调时则在‘0’和‘1’直接设置多个门限,使得接收比特可以投射到范围内的某个区域里,而通过区域比特的组合信息,使用欧几何距离(用一定概率值分析接收比特信息)计算最准确的接收比特,这样,如果产生错码,软判决纠正错码的距离将变小(图b中实点位置,纠正错码距离提升),从而得到相对准确的接收比特。因此,软判决的解码过程误码率性能将优于硬判决。


如果这篇文章帮助到了你,你可以请作者喝一杯咖啡




