指数移动平均(EMA)的原理及PyTorch实现
【炼丹技巧】
在深度学习中,经常会使用EMA(指数移动平均)这个方法对模型的参数做平均,以求提高测试指标并增加模型鲁棒。
今天瓦砾准备介绍一下EMA以及它的Pytorch实现代码。
EMA的定义
指数移动平均(Exponential Moving Average)也叫权重移动平均(Weighted Moving Average),是一种给予近期数据更高权重的平均方法。
假设我们有n个数据:
- 普通的平均数:
- EMA:
,其中,
表示前
条的平均值 (
),
是加权权重值 (一般设为0.9-0.999)。
Andrew Ng在Course 2 Improving Deep Neural Networks中讲到,EMA可以近似看成过去 个时刻
值的平均。
普通的过去 时刻的平均是这样的:
类比EMA,可以发现当 时,两式形式上相等。需要注意的是,两个平均并不是严格相等的,这里只是为了帮助理解。
实际上,EMA计算时,过去 个时刻之前的数值平均会decay到
的加权比例,证明如下。
如果将这里的 展开,可以得到:
其中, ,代入可以得到
。
在深度学习的优化中的EMA
上面讲的是广义的ema定义和计算方法,特别的,在深度学习的优化过程中, 是t时刻的模型权重weights,
是t时刻的影子权重(shadow weights)。在梯度下降的过程中,会一直维护着这个影子权重,但是这个影子权重并不会参与训练。基本的假设是,模型权重在最后的n步内,会在实际的最优点处抖动,所以我们取最后n步的平均,能使得模型更加的鲁棒。
EMA的偏差修正
实际使用中,如果令 ,且步数较少,ema的计算结果会有一定偏差。
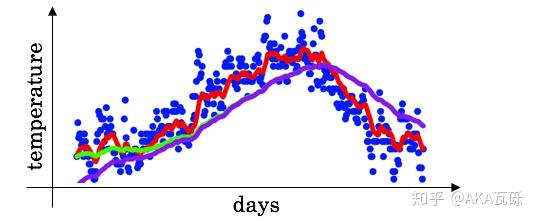
理想的平均是绿色的,因为初始值为0,所以得到的是紫色的。
因此可以加一个偏差修正(bias correction):
显然,当t很大时,修正近似于1。
EMA为什么有效
网上大多数介绍EMA的博客,在介绍其为何有效的时候,只做了一些直觉上的解释,缺少严谨的推理,瓦砾在这补充一下,不喜欢看公式的读者可以跳过。
令第n时刻的模型权重(weights)为 ,梯度为
,可得:
令第n时刻EMA的影子权重为 ,可得:
代入上面 的表达,令
展开上面的公式,可得:
对比两式:
EMA对第i步的梯度下降的步长增加了权重系数 ,相当于做了一个learning rate decay。
PyTorch实现
瓦砾看了网上的一些实现,使用起来都不是特别方便,所以自己写了一个。
class EMA():
def __init__(self, model, decay):
self.model = model
self.decay = decay
self.shadow = {}
self.backup = {}
def register(self):
for name, param in self.model.named_parameters():
if param.requires_grad:
self.shadow[name] = param.data.clone()
def update(self):
for name, param in self.model.named_parameters():
if param.requires_grad:
assert name in self.shadow
new_average = (1.0 - self.decay) * param.data + self.decay * self.shadow[name]
self.shadow[name] = new_average.clone()
def apply_shadow(self):
for name, param in self.model.named_parameters():
if param.requires_grad:
assert name in self.shadow
self.backup[name] = param.data
param.data = self.shadow[name]
def restore(self):
for name, param in self.model.named_parameters():
if param.requires_grad:
assert name in self.backup
param.data = self.backup[name]
self.backup = {}
# 初始化
ema = EMA(model, 0.999)
ema.register()
# 训练过程中,更新完参数后,同步update shadow weights
def train():
optimizer.step()
ema.
