浮点运算：双精度、单精度、半精度浮点数计算（FP16/FP32/FP64），浮点和定点

1.实数数的表示

参考深入理解C语言-03-有符号数，定点数，浮点数

1.1定点数

一般在没有FPU寄存器的嵌入式系统中使用比较多。比如常见的32位系统中，将高16位作为整数部分，低16位作为小数部分。
这样就可以用整数来模拟定点数的 +  - * / 运算。
关于定点数的数学分析，请参考以下文档：
http://www.digitalsignallabs.com/fp.pdf

代码实现可以参考以下文档：
http://www.eetimes.com/author.asp?section_id=36&doc_id=1287491

1.2浮点数

格式：

         s符号位  exp指数   frac尾数   精度说明

16位       1            5             11            半精度 FP16
32位       1            8             23            单精度 FP32
64位       1           11            52            双精度 FP64
11位       1            4             6              没找到应用 11bit存储起来也奇怪

表示的数为： (-1)的s次方 *  2的(exp -base)次方 * (1 + frac)
base = 2的(exp位数 -1) -1 对于32位，为127 = 2的7次方 -1

比如0.325 =1.3 / 4  （规范化，这种方式在信息处理中很常见）
则s为0， exp为 127 + (-2) = 125, frac为0.3
近一步把0.3表示为  1/4 + 1/20 = (1/4) * ( 1 + 1/5)
注意到1/5可以表示为 (3/16) / (1 - 1/16) = (3/16) ( 1 + 1/16 + (1/16)*(1/16) + ... (无穷级数展开)
对应的二进制表示为
0.  01  (0011) (0011) ...
取前23位，则为：
0100110 01100110 01100110

这样，0.325在内存中的2进制表示为：
0  01111101  0100110 01100110 01100110

对应16进制为：3E A6 66 66

2.精度说明

半精度 16bit，单精度32bit，双精度64，上文已经提出，需要注意的是FP16，FP32，FP64都有隐藏的起始位。

参考程序员必知之浮点数运算原理详解

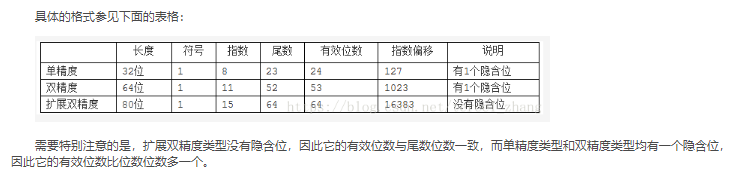
以半精度FP16为例说明

2.1半精度FP16

3.浮点运算加法和乘法

相比于整数加法和乘法多了比较，移位逻辑，比整数复杂很多

3.1加法

       浮点加法器首先对浮点数拆分，得到符号、阶码、尾数。对拆分结果进行绝对值比较，得到大的阶码、阶差和比较结果输出。然后进行对阶，通过移位小的尾数，得到相同大阶。对尾数进行尾数加减运算，得到的结果进行规格化，最后结合规格化结果运算结果符号输出，得到结果输出。

        一.需要注意一个是以绝对值大的对阶数(exponent), 二.对结果规格化规划到(1+Frac)的形式。

3.2乘法

       符号位只是两者的异或，指数位基本上是两指数的相加，而尾数位就需要在正常的乘法之余考虑到移位（和随之而来的指数为的溢出）和进位的情况。

原文链接：https://blog.csdn.net/cy413026/article/details/101457312

---

 

浮点数是计算机上最常用的数据类型之一，有些语言甚至数值只有浮点型（Perl，Lua同学别跑，说的就是你）。

常用的浮点数有双精度和单精度。除此之外，还有一种叫半精度的东东。

双精度64位，单精度32位，半精度自然是16位了。

半精度是英伟达在2002年搞出来的，双精度和单精度是为了计算，而半精度更多是为了降低数据传输和存储成本。

很多场景对于精度要求也没那么高，例如分布式深度学习里面，如果用半精度的话，比起单精度来可以节省一半传输成本。考虑到深度学习的模型可能会有几亿个参数，使用半精度传输还是非常有价值的。

Google的TensorFlow就是使用了16位的浮点数，不过他们用的不是英伟达提出的那个标准，而是直接把32位的浮点数小数部分截了。据说是为了less computation expensive。。。

比较下几种浮点数的layout:

双精度浮点数

 

 

单精度浮点数

 

 

半精度浮点数

 

 

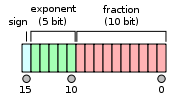
它们都分成3部分，符号位，指数和尾数。不同精度只不过是指数位和尾数位的长度不一样。

解析一个浮点数就5条规则

如果指数位全零，尾数位是全零，那就表示0
如果指数位全零，尾数位是非零，就表示一个很小的数（subnormal），计算方式 (−1)^signbit × 2^−126 × 0.fractionbits
如果指数位全是1，尾数位是全零，表示正负无穷
如果指数位全是1，尾数位是非零，表示不是一个数NAN
剩下的计算方式为 (−1)^signbit × 2^(exponentbits−127) × 1.fractionbits
常用的语言几乎都不提供半精度的浮点数，这时候需要我们自己转化。

具体可以参考Numpy里面的代码：

https://github.com/numpy/numpy/blob/master/numpy/core/src/npymath/halffloat.c#L466

当然按照TensorFlow那么玩的话就很简单了(~摊手~)。

参考资料：

https://en.wikipedia.org/wiki/Half-precision_floating-point_format

https://en.wikipedia.org/wiki/Double-precision_floating-point_format

https://en.wikipedia.org/wiki/Single-precision_floating-point_format

http://download.tensorflow.org/paper/whitepaper2015.pdf
————————————————
版权声明：本文为CSDN博主「AI图哥」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/sinat_24143931/article/details/78557852