赏月斋源码共享计划 第五期 最小覆盖子串

'''
给你一个字符串 S、一个字符串 T，请在字符串 S 里面找出：包含 T 所有字符的最小子串。

示例：

输入: S = "ADOBECODEBANC", T = "ABC"
输出: "BANC"
说明：

如果 S 中不存这样的子串，则返回空字符串 ""。
如果 S 中存在这样的子串，我们保证它是唯一的答案。
'''

# 思路：滑动窗口适合求'连续'问题
# left, right, 如果窗口里面不符合条件，right+1， 如果符合，收缩左边的窗口，left+1

class Solution:
    def minWindow(self, s: str, t: str) -> str:
        # requires: T 的字典
        # windows：窗口的字典
        def is_valid(requires, windows):
            for key, value in requires.items():
                if windows.get(key,0) < value:
                    return False
            return True

        if not s or not t: return ''
        N = len(s)
        requires = {}
        for item in t:
            requires[item] = requires.get(item, 0) + 1        

        # 滑动窗口
        windows = {s[0]:1}
        left, right = 0, 0
        ret_len, ret = N, ''
        while right < N:
            if is_valid(requires, windows):
                if right-left+1 <= ret_len:
                    ret_len = right-left+1
                    ret = s[left: right+1]
                windows[s[left]] -= 1
                left += 1
            else:
                right += 1
                if right < N: # !!!!
                    windows[s[right]] = windows.get(s[right], 0) + 1
        return ret

　　

 

方法一：滑动窗口
思路和算法

本问题要求我们返回字符串 ss 中包含字符串 tt 的全部字符的最小窗口。我们称包含 tt 的全部字母的窗口为「可行」窗口。

我们可以用滑动窗口的思想解决这个问题，在滑动窗口类型的问题中都会有两个指针。一个用于「延伸」现有窗口的 rr 指针，和一个用于「收缩」窗口的 ll 指针。在任意时刻，只有一个指针运动，而另一个保持静止。我们在 ss 上滑动窗口，通过移动 rr 指针不断扩张窗口。当窗口包含 tt 全部所需的字符后，如果能收缩，我们就收缩窗口直到得到最小窗口。

 

 

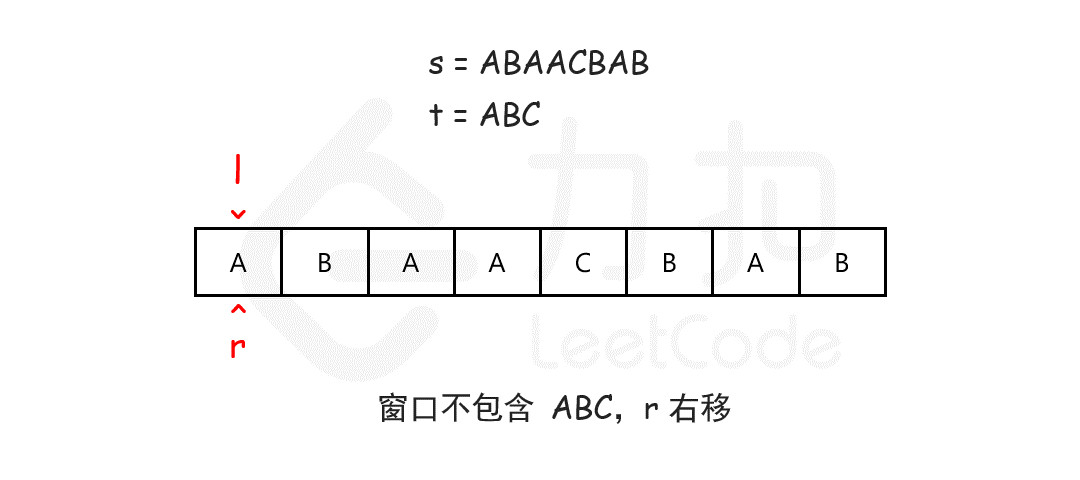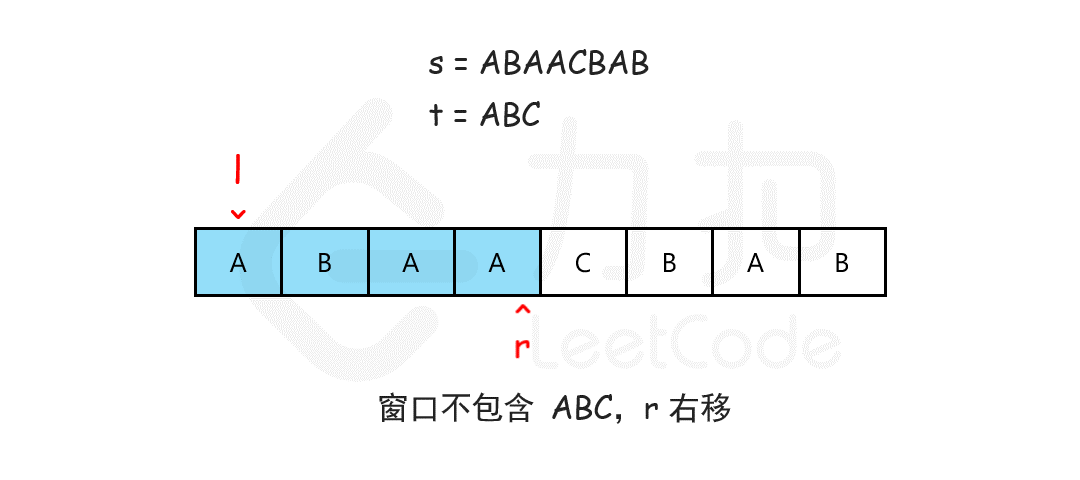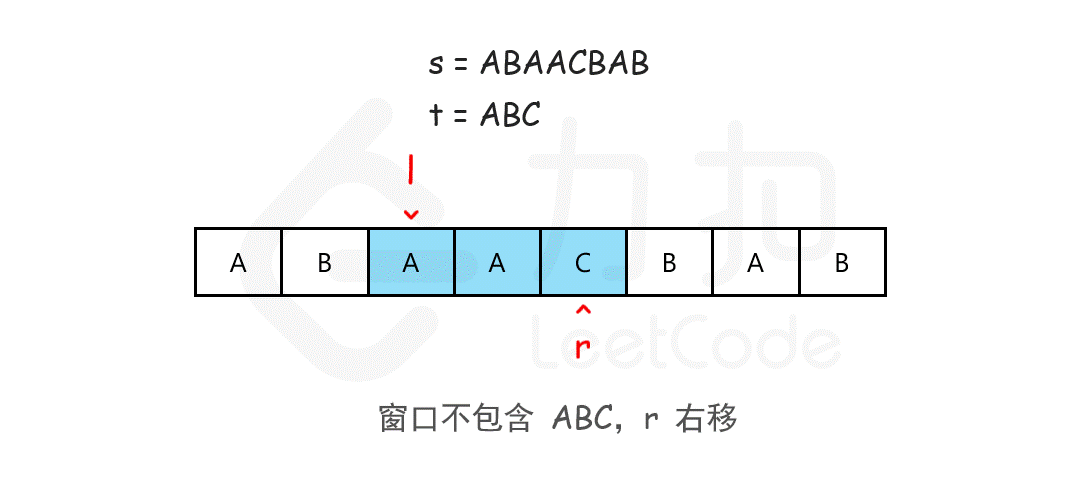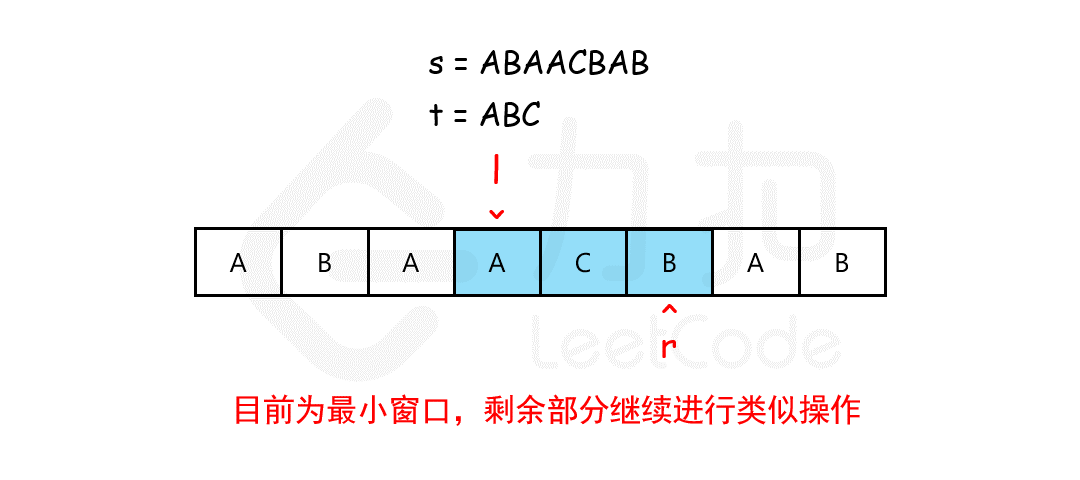
如何判断当前的窗口包含所有 tt 所需的字符呢？我们可以用一个哈希表表示 tt 中所有的字符以及它们的个数，用一个哈希表动态维护窗口中所有的字符以及它们的个数，如果这个动态表中包含 tt 的哈希表中的所有字符，并且对应的个数都不小于 tt 的哈希表中各个字符的个数，那么当前的窗口是「可行」的。

注意：这里 tt 中可能出现重复的字符，所以我们要记录字符的个数。

考虑如何优化？ 如果 s =  XX ... ... XABCXXXX = XX ⋯ XABCXXXX， t=ABC，那么显然 [XX⋯XABC] 是第一个得到的「可行」区间，得到这个可行区间后，我们按照「收缩」窗口的原则更新左边界，得到最小区间。我们其实做了一些无用的操作，就是更新右边界的时候「延伸」进了很多无用的 X，更新左边界的时候「收缩」扔掉了这些无用的 X，做了这么多无用的操作，只是为了得到短短的 ABC。没错，其实在 ss 中，有的字符我们是不关心的，我们只关心 tt 中出现的字符，我们可不可以先预处理 ss，扔掉那些 tt 中没有出现的字符，然后再做滑动窗口呢？也许你会说，这样可能出现 XXABXXC 的情况，在统计长度的时候可以扔掉前两个 X，但是不扔掉中间的 X，怎样解决这个问题呢？优化后的时空复杂度又是多少？

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/minimum-window-substring/solution/zui-xiao-fu-gai-zi-chuan-by-leetcode-solution/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。