小世界网络

在网络理论中，小世界网络是一类特殊的复杂网络结构，在这种网络中大部分的节点彼此并不相连，但绝大部分节点之间经过少数几步就可到达。

在日常生活中，有时你会发现，某些你觉得与你隔得很“遥远”的人，其实与你“很近”。小世界网络就是对这种现象（也称为小世界现象）的数学描述。用数学中图论的语言来说，小世界网络就是一个由大量顶点构成的图，其中任意两点之间的平均路径长度比顶点数量小得多。除了社会人际网络以外，小世界网络的例子在生物学、物理学、计算机科学等领域也有出现。许多经验中的图可以由小世界网络来作为模型。万维网、公路交通网、脑神经网络和基因网络都呈现小世界网络的特征。

小世界网络最早是由邓肯·瓦茨（Duncan Watts）和斯蒂文·斯特罗加茨（Steven Strogatz）在1998年引进的，将高集聚系数和低平均路径长度作为特征，提出了一种新的网络模型，一般就称作瓦茨-斯特罗加茨模型（WS模型），这也是最典型的小世界网络的模型。

源起

小世界网络的概念是随着对复杂网络的研究而出现的。“网络”其实就是数学中图论研究的图，由一群顶点以及它们之间所连的边构成。在网络理论中则换一套说法，用“节点”代替“顶点”，用“链接”代替“边”。复杂网络的概念，是用来描述由大量节点以及这些节点之间错综复杂的联系所构成的网络。这样的网络会出现在简单网络中没有的特殊拓扑特性。

自二十世纪60年代开始，对复杂网络的研究主要集中在随机网络上。随机网络，又称随机图，是指通过随机过程制造出的复杂网络。最典型的随机网络是保罗·埃尔德什和阿尔弗雷德·雷尼提出的ER模型。ER模型是基于一种“自然”的构造方法：假设有{\displaystyle n}个节点，并假设每对节点之间相连的可能性都是常数{\displaystyle 0<p<1}。这样构造出的网络就是ER模型网络。科学家们最初使用这种模型来解释现实生活中的网络。

六度分隔理论

主条目：六度分隔理论

最早观察到小世界现象的是社会人际网络。将每个人作为节点，将人与人之间的人际关系（朋友，合作，相识等）作为链接，就创建起一个社会人际网络。有时你会发现，在这样一个社会网络中，某些你觉得与你隔得很“遥远”的人，其实与你“很近”：你很喜欢的一位知名作家的弟弟，其实是你旧时同班同学的男友；你跳槽到的新企业的总裁的侄子，会定期找你一个医生朋友就医；甚至和一个偶遇的陌生人聊天时，你发现你们都参加过某教授的讲座，都认识某餐厅的老板娘等等。你会感叹：“这个世界真小。”对于世界上任意两个人，通过这样第三者、第四者的间接关系来创建联系的话，平均需要多少人呢？

二十世纪60年代，美国哈佛大学社会心理学家斯坦利·米尔格伦（Stanley Milgram）做了一个连锁信实验。他将一些信件交给自愿的参加者，要求他们通过自己的熟人将信传到信封上指明的收信人手里，他发现，296封信件中有64封最终送到了目标人物手中。而在成功传递的信件中，平均只需要5次转发，就能够到达目标。也就是说，在社会网络中，任意两个人之间的“距离”是6^[1]。这就是所谓的“六度分隔”理论。尽管他的实验有不少缺陷，但这个现象引起了学界的注意。

凯文贝肯游戏与埃尔德什数

主条目：埃尔德什数

继米尔格伦的实验后，为了检验六度分隔理论的真实性，人们又进行了一些其它实验。其中一个著名的例子是“凯文·贝肯游戏”（game of Kevin Bacon）。这个游戏的主角是美国电影演员凯文·贝肯，游戏的方法是通过不停地寻找共同出演同一电影的演员，最终“找到”另一个“目标”演员。游戏里每一个演员都有一个“贝肯数”：如果一个演员与贝肯合作过电影，那么他（她）的“贝肯数”就是1。如果一个演员没有与贝肯合作过，但与某个“贝肯数”为1的演员合作过，那么他（她）的贝肯数”就是2，以此类推。比如说，吴彦祖在《80天环游世界》中与卢克·威尔逊合作过，卢克·威尔逊在《家有跳狗》中与与贝肯合作过，所以吴彦祖的“贝肯数”是2^[2]。对超过133万名世界各地的演员的统计得出，他们平均的“贝肯数”是2.981^[3]，最大的也仅仅是8^[4]。

一个类似的结果是数学界中的“埃尔德什数”。保罗·埃尔德什就是随机图理论的开创者之一，他是著名的数学家。与他一起发表过论文的学者的“埃尔德什数”是1，与这些学者合作发表过论文的学者的“埃尔德什数”是2，以此类推。美国数学会的数据库中记录的超过40万名数学家们的“埃尔德什数”平均是4.65，最大的是13^[5]。

定义

米尔格伦实验、凯文贝肯游戏、埃尔德什数以及一些类似的实验证明了，在现实世界里的一些网络中，尽管节点数量庞大，但从一点出发，其实只需要经过仅仅几步转折，就能到达任一个节点。1998年，美国康奈尔大学的博士生邓肯·瓦茨（Duncan Watts）和他的导师斯蒂文·斯特罗加茨（Steven Strogatz）发表了一篇名为《小世界网络的集体动力学》（Collective dynamics of the 'Small World' networks）的论文^[6]。他们把这种现象归类为某一类复杂网络的特性。他们注意到复杂网络可以按两个独立的结构特性分类，就是集聚系数和节点间的平均路径长度。

平均路径长度

平均路径长度也称为特征路径长度或平均最短路径长度，指的是一个网络中两点之间最短路径长度（或称距离）的平均值。从一个节点{\displaystyle s_{i}}出发，经过与它相连的节点，逐步“走”到另一个节点{\displaystyle s_{j}}所经过的路途，称为两点间的路径。其中最短的路径也称为两点间的距离，记作{\displaystyle \operatorname {dist} (i,j)}。而平均路径长度定义为：

{\displaystyle \operatorname {dist} _{c}={\frac {2}{N(N+1)}}\sum _{i\leqslant N}\sum _{j\geqslant i}\operatorname {dist} (i,j)}

这其中{\displaystyle N}是节点数目，并定义节点到自身的最短路径长度为0。如果不计算到自身的距离，那么平均路径长度的定义就变成^[7]：

{\displaystyle \operatorname {dist} _{c}={\frac {2}{N(N-1)}}\sum _{i\leqslant N}\sum _{j>i}\operatorname {dist} (i,j)}

集聚系数

主条目：集聚系数

集聚系数（也称群聚系数、集群系数）是用来描述图或网络中的顶点（节点）之间结集成团的程度的系数。具体来说，是一个点的邻接点之间相互连接的程度。例如在社交网络中，你的朋友之间相互认识的程度^[8]。一个节点{\displaystyle s_{i}}的集聚系数 {\displaystyle C(i)} 等于所有与它相连的顶点相互之间所连的边的数量，除以这些顶点之间可以连出的最大边数^[9]。显然 {\displaystyle C(i)} 是一个介于0与1之间的数。{\displaystyle C(i)} 越接近1，表示这个节点附近的点越有“抱团”的趋势。

介于随机与规则之间

对于纯粹的规则网络，当其中连接数量接近饱和时，集聚系数很高，平均路径长度也十分短。例如完全耦合网络（即完全图），每两个节点之间都相连，所以集聚系数是1，平均路径长度是1。然而，现实中的复杂网络是稀疏的，连接的个数只是节点数的若干倍（{\displaystyle {\mathcal {O}}(N)}），远远不到饱和。如果考虑将节点排列成正多边形，每各节点都只与距离它最近的 {\displaystyle 2K} 个节点相连，那么在{\displaystyle K}比较大，但仍然保证{\displaystyle K<{\frac {2}{3}}N}时，其集聚系数为：

{\displaystyle C(i)={\frac {3(K-2)}{4(K-1)}}\approx {\frac {3}{4}}}

虽然能保持高集聚系数，但平均路径长度为：

{\displaystyle \operatorname {l} _{avg}\approx {\frac {N}{4K}}={\mathcal {O}}(N)}

平均路径长度与节点数成正比。

纯粹的随机网络（如ER随机网络模型）有着很小的平均路径长度，但同时集聚系数也很小。可是现实中的不少网络虽然有很小的平均路径长度，但却也有着比随机网络高出相当多的集聚系数。因此瓦茨和斯特罗加茨认为，现实中的复杂网络是一种介于规则网络和随机网络之间的网络。他们把这种特性称为现实网络的小世界特性，就是：

1. 有很小的平均路径长度：在节点数{\displaystyle N}很大时，平均路径长度近似于

   {\displaystyle \operatorname {dist} _{c}\propto \log(N)}^[10]

2. 有很高的集聚系数：集聚系数大约和规则网络在同一数量级，远大于随机网络的集聚系数^[11]。

瓦茨-斯特罗加茨模型

在1998年的同一篇论文中，瓦茨和斯特罗加茨提出了一个模型来解释小世界网络，后来被称为瓦茨-斯特罗加茨模型（简称WS模型）。WS模型是基于两人的一个假设：小世界模型是介于规则网络和随机网络之间的网络。因此模型从一个完全的规则网络出发，以一定的概率将网络中的连接打乱重连。具体的构造如下：

1. 首先从一个规则的网络开始。这个网络中的{\displaystyle N}个节点排成正多边形，每个节点都与离它最近的{\displaystyle 2K}个节点相连。其中{\displaystyle K}是一个远小于{\displaystyle N}的正整数。
2. 选择网络中的一个节点，从它开始（它自己是1号节点）将所有节点顺时针编号，再将每个节点连出的连接也按顺时针排序。然后，1号节点的第1条连接会有{\displaystyle 0<p<1}的概率被重连。重连方式如下：保持1号节点这一端不变，将连接的另一端随机换成网络里的另一个节点，但不能使得两个节点之间有多于1个连接。
3. 重连之后，对2号、3号节点也做同样的事（如果这其中有连接已经有过重连的机会，就不再重复），直到绕完一圈为止。
4. 再次从1号节点的第2条连接开始，重复第2个步骤和第3个步骤，直到绕完一圈为止。
5. 再次从1号节点开始，重复第4个步骤，直到所有的连接都被执行过第2个步骤（重连的步骤）。

由于{\displaystyle NK}个连接里每个连接都恰好有一次重连的机会，所以这个过程最后总会结束。最后得到的网络称为WS模型网络^[6][12]。

 

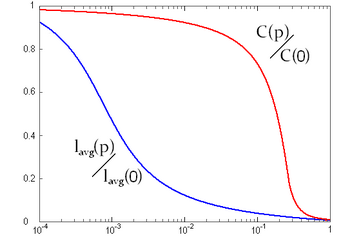
WS模型的集聚系数C（红色）与平均路径长度L(蓝色)随{\displaystyle p}变化的图像

如果概率{\displaystyle p=0}，那么重连永远不会发生，最后得到的是原来的规则网络。如果概率{\displaystyle p=1}，那么所有的连接都被重连了一次，最后得到的是一个完全的随机网络。而对于概率{\displaystyle 0<p<1}的时候，瓦茨和斯特罗加茨考察了集聚系数和平均路径长度与{\displaystyle p}的关系，将这两者看作是关于{\displaystyle p}的函数：集聚系数{\displaystyle C=C(p)}，平均路径长度{\displaystyle \operatorname {l} _{avg}=\operatorname {l} _{avg}(p)}^[6]。他们发现，在{\displaystyle p}从0变到1的过程中，{\displaystyle \operatorname {l} _{avg}(p)}下降得很快，而{\displaystyle C(p)}下降的比较慢。右侧是演示这个关系的一个示意图。图中的横轴是{\displaystyle p}（使用对数坐标轴表示），纵轴是比值（介乎0与1之间）。蓝色曲线表示{\displaystyle \operatorname {l} _{avg}(p)}与{\displaystyle \operatorname {l} _{avg}(0)}之比，红色曲线表示{\displaystyle C(p)}与{\displaystyle C(0)}之比。从右图可以看到，蓝色曲线很快就逐渐下降到0.2以下，而红色曲线则直到超过{\displaystyle p=10^{-1}}后才开始有显著下降。当{\displaystyle p=10^{-1}}的时候，{\displaystyle C(p)}大概还有{\displaystyle C(0)}八成左右，但{\displaystyle \operatorname {l} _{avg}(p)}只占{\displaystyle \operatorname {l} _{avg}(0)}的不到百分之5了。所以对于很小的{\displaystyle p}，{\displaystyle \operatorname {l} _{avg}(p)}可以很小，但{\displaystyle C(p)}可以很大。这正是小世界网络的特征^[6][13]。

更精确的计算^[14]指出WS模型的集聚系数是：

{\displaystyle C(p)={\frac {3(K-1)}{2(2K-1)}}(1-p)^{3}}

而平均路径长度则尚未有精确表达式^[15]。

纽曼-瓦茨模型

不久之后，瓦茨又与英国物理学家提出了另一个稍有不同的模型，称为纽曼-瓦茨模型（NW模型）。其中将重连变成添加链接^[16]。具体的构造方法是：第一步与WS模型相同，都是先创建一个规则网络；然后随机选择一对尚未连接的节点，设定有{\displaystyle 0<p<1}的概率产生连接。这样重复一定次数，但不允许两节点之间有多于一条连接，也不允许节点与自身相连。

纽曼-瓦茨模型在理论分析上比瓦茨-斯特罗加茨模型要简单一点。当 {\displaystyle p} 很小而 {\displaystyle N} 很大的时候，这两个模型本质上是一样的^[17]。

小世界网络的性质

由于小世界网络具有高集聚系数，它的结构中不可避免地会有许多团（彼此之间两两相连的一小群节点）以及只比团差几个连接的节点群。另一方面，任两个结点大多会以至少一条短路径连接着。这是要求有小的最短路径长度平均值的结果。此外，小世界网络常连带地具有一些性质，不过这些性质并不是作为这类网络非有不可的。很典型的是这类网络常常会出现“枢纽”（与很多节点都相连的节点）。

相关条目

• 无尺度网络
• 可导航网络

参考来源

1. ^ 《复杂网络理论及其应用》，第5页
2. ^ The Oracle of Bacon. Patrick Reynolds. [2011-07-12].
3. ^ The Oracle of Bacon. Patrick Reynolds. [2011-07-12].
4. ^ 《复杂网络理论及其应用》，第6页
5. ^ 《复杂网络理论及其应用》，第6-7页
6. ^ 跳转至：^{6.0 6.1 6.2 6.3} Watts DJ, Strogatz SH. Collective dynamics of 'small-world' networks (PDF). Nature. June 1998, 393 (6684): 440–442. Bibcode:1998Natur.393..440W. PMID 9623998. doi:10.1038/30918. （原始内容 (PDF)存档于2007-04-18）.
7. ^ S.Boccaletti, 第182页
8. ^ 王冰、修志龙、唐焕文. 基于复杂网络理论的代谢网络结构研究进展 (PDF). 《中国生物工程杂志》. 2005 No.6, 25–3: 10–14.
9. ^ 章忠志、荣莉莉、周涛. 一类无标度合作网络的演化模型 (PDF). 《系统工程理论与实践》. 2005年11月, 11: 55–60.
10. ^ S.Boccaletti，第193页
11. ^ The structure and dynamics of networks, 第286页
12. ^ 《复杂网络与应用》第21页
13. ^ 《复杂网络与应用》第22页
14. ^ A. Barrat, M. Weigt. On the properties of small-world network models. The European Physical Journal B: 547–560. doi:10.1007/s100510050067.
15. ^ 《复杂网络与应用》第23页
16. ^ M. E. J. Newman, D. J. Watts. Renormalization group analysis of the small-world network model. Phys. Lett. A: 341–346. doi:10.1016/S0375-9601(99)00757-4.
17. ^ 《复杂网络理论及其应用》，第22页

• 汪小帆,李翔,陈关荣. 《复杂网络理论及其应用》. 清华大学出版社. 2006. ISBN 9787302125051 （中文）.
• 黄萍,张许杰,刘刚. 《小世界网络的研究现状与展望》. 情报杂志 （中文）.
• Mark E. J. Newman,Duncan J. Watts. The structure and dynamics of networks. Princeton University Press. 2006. ISBN 978-0691113579 （英语）.
• Stefano Boccaletti, V. Latora, Y. Moreno, M. Chavez, D. Hwang. Complex networks: structure and dynamics. Volume 424, No 4-5 (2006.02). Elsevier Physics Report. doi:10.1016/j.physrep.2005.10.009 （英语）.
• Richard Durrett. Random graph dynamics. Cambridge University Press. 2007. ISBN 978-0-521-86656-9 （英语）.