1651. Shortest Subchain

1651. Shortest Subchain

Time limit: 1.0 second Memory limit: 64 MB

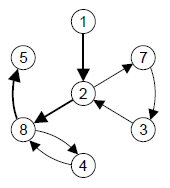
A chain p is given in a directed graph without loops or multiple edges. It is required to specify its subchain q such that

• the initial and final vertices of the chains p and q coincide;
• the edges in the chain q are in the same order as in the chain p;
• the chain q has the minimal possible number of edges under the given conditions.

Input

The chain p is given by the list of its vertices. The first line contains the number n of vertices in the list, 2 ≤ n ≤ 100000 (thus, the length of the chain is n−1). The following lines contain n numbers of vertices (they are integers in the range from 1 to 10000). The numbers are separated by spaces or linebreaks. No two successive vertices in the list coincide.

Output

Output the vertices of the chain q by giving their numbers separated by a space. Chain q may consist of single a vertex.

Sample

input	output
9 1 2 7 3 2 8 4 8 5	1 2 8 5

Problem Author: Vladimir Yakovlev (idea by Magaz Asanov) Problem Source: NEERC 2008, Eastern subregion quarterfinals

***************************************************************************************

图论中的dp，路径更新

***************************************************************************************

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<vector>
#include<algorithm>
#include<stack>
using namespace std;
int used[100001];//表示点被用时所在的位置
int dp[100001];//求最短路径数组
int base[100001];//输入原始数据
int path[100001];//记录选择的点所在的位置
int n,i,j,k;
void  findpath(int x)//输出路径
  {
      if(x==-1)
      return;
      cout<<base[x]<<' ';
      findpath(path[x]);
  }
int main()
{
    cin>>n;
    for(i=1;i<=n;i++)
     cin>>base[i];
    memset(used,-1,sizeof(used));
    memset(path,-1,sizeof(path));
    used[base[n]]=n;
    dp[n]=0;
    for(i=n-1;i>=1;i--)
     {
         if(used[base[i]]==-1)//没有用时就选择
          {
              dp[i]=dp[i+1]+1;
              used[base[i]]=i;
              path[i]=i+1;
          }
          else
            {
                if(dp[used[base[i]]]>=dp[i+1]+1)//用过以后比较、更新
               {
                 dp[i]=dp[i+1]+1;
                 path[i]=i+1;
                 used[base[i]]=i;//点更新到最优位置
               }
             else
              {
                  dp[i]=dp[used[base[i]]];
                  path[i]=path[used[base[i]]];//路径更新到最优位置
              }
            }
     }
     //cout<<dp[1]<<endl;
     findpath(1);
     cout<<endl;
     return 0;
}