微分方程的隐式方法

微分方程的隐式方法 Implicit Methods for Differential Equations

1. 隐式方法

• 我们在这些笔记的第一部分中看到的求解微分方程的方法（例如欧拉法，中点法）都被称为求解ODE的“显式”方法。
  但是，有时 ODE 可能会变得“僵硬”，在这种情况下，显式方法在解决它们方面做得并不好。只要有可能，最好改变你的问题公式，以便你不必解决僵硬的ODE。然而，有时这是不可能的，你只需要能够解决僵硬的ODE。如果是这种情况，您通常必须使用“隐式”的 ODE 解决方案方法。

1.1 僵硬ODE的示例 Example Stiff ODE

• 首先，刚性方程的含义和原因是什么？让我们考虑一个在动力学中经常出现的例子。假设我们有一个粒子，位置为（x（t），y（t）），并假设我们希望y坐标始终为零。一种方法是将分量 −ky（t） 添加到 y ̇（t） 中，其中 k 是一个大的正常数。如果 k 足够大，则粒子永远不会偏离 y（t） = 0 太远，因为 −ky（t） 项总是使 y（t） 回到零。但是，让我们假设对x坐标没有限制，并且我们希望用户能够沿着x轴任意拉动粒子。因此，让我们假设在一段时间内，我们的微分方程只是

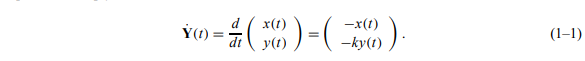
（我们还假设粒子不完全以 y0 = 0 开头。这里发生的事情是，粒子被 y = 0 线强烈吸引，而对 x = 0 的吸引力则不那么强烈。如果我们在时间上足够远地求解 ODE，我们预计粒子的位置将收敛到 （0， 0） 和
然后一旦到达就呆在那里。
现在假设我们使用欧拉的方法来求解方程。如果我们采取大小为h的一步，我们得到

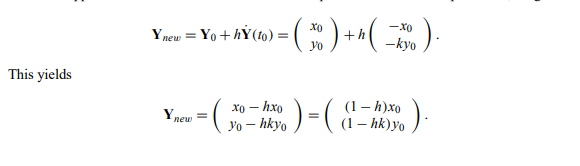
如果我们看一下这个等式的y分量，我们会看到如果|1 − hk|> 1，则我们计算的 ynew 将具有大于 |y0| 的绝对值。换句话说，如果|1 − hk|>1，欧拉的方法不会收敛到一个答案：每一步都会得到一个大于上一个的ynew值。从技术上讲，欧拉的方法对于|1−hk是不稳定的|> 1.因此，如果我们希望收敛，我们最好有 1−hk > −1 或 hk < 2。我们希望采取的最大步长小于2/ k。

• 现在，如果k是一个大数，我们将不得不采取非常小的步骤。这意味着粒子非常缓慢地滑向（0，0）。即使粒子可能几乎满足y0 = 0，我们也必须采取如此小的步骤，以至于粒子沿着x轴的行进几乎不存在。这就是僵硬的ODE的体现。在这种情况下，刚度产生于使k非常大，以保持粒子接近线y = 0。稍后，当我们将具有二阶动力学的粒子与弹簧连接在一起时，我们将体验到完全相同的效果：僵硬的ODE。即使我们使用更复杂的显式方法，例如四阶Runge-Kutta，我们可能会在步骤的大小上做得更好一些，但我们仍然会遇到重大问题。

• 现在，正如我们上面所说，游戏的名称是提出您的动态问题，以便您不会遇到僵硬的ODE。但是，当您无法做到时，您将不得不转向隐式解决方案方法。我们将在下面展示的方法是最简单的隐式方法，它基于“向后”迈出欧拉一步。

1.2 解决僵硬的ODE

• 不使用Ynew = Y0 + h f（Y（t0）），而是使用公式

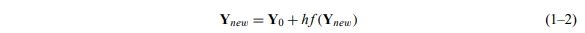
• 也就是说，我们将在目标点评估f，而不是我们来自哪里。（如果你考虑逆转世界，把一切都倒过来，上面的等式是完全有道理的。然后等式说：“如果你在Ynew，并且迈出了一步-hf（Ynew），你最终会到达Y0。因此，如果你的微分方程代表了一个在时间上可逆的系统，那么这一步是有道理的。它只是找到一个点Ynew，这样如果你倒流时间，你最终会到达Y0。所以，我们正在寻找一个Ynew，这样f，在那里评估，乘以h，直接指向我们来自哪里。不幸的是，我们通常不能求解Ynew，除非f碰巧是线性函数。
• 为了解决这个问题，我们将用线性近似替换f（Ynew），同样基于f的泰勒级数。让我们定义 ΔY, ΔY = Ynew − Y0。使用这个，我们将等式（1-2）重写为

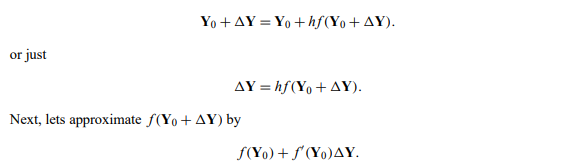
（请注意，由于 f（Y0） 是一个向量，因此导数 f'（Y0） 是一个矩阵。使用这个近似值，我们可以近似ΔY

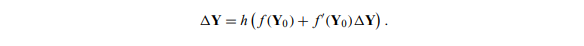
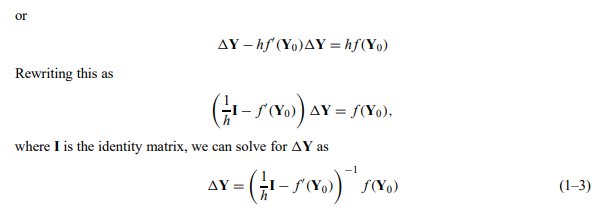
• 计算Ynew = Y0 + 1Y显然比使用显式方法更费力，因为我们必须在每一步求解线性系统。虽然这似乎是一个严重的弱点，但从计算上讲，不要绝望（还）。对于许多类型的问题，矩阵 f' 将是稀疏的——例如，如果我们模拟一个弹簧晶格，f' 将具有与粒子连通性相匹配的结构。因此，通常可以在线性时间（即与Y的维度成比例的时间）中求解方程（1-3）。在这种情况下，回报是戏剧性的：我们通常可以采取相当大的时间步长而不会失去稳定性（即没有发散，就像如果步长太大，则在显性情况下发生的那样）。因此，求解每个线性系统所花费的时间被一个事实所抵消，即我们的时间步长通常比我们使用显式方法管理的时间大几个数量级。（当然，完成所有这些操作所需的代码比显式情况要复杂得多，就像我们说的，如果可以的话，让你的问题变得不僵硬，如果没有，就付出代价。让我们将隐式方法应用于等式 （1–1）。我们有 f（Y（t）） 是

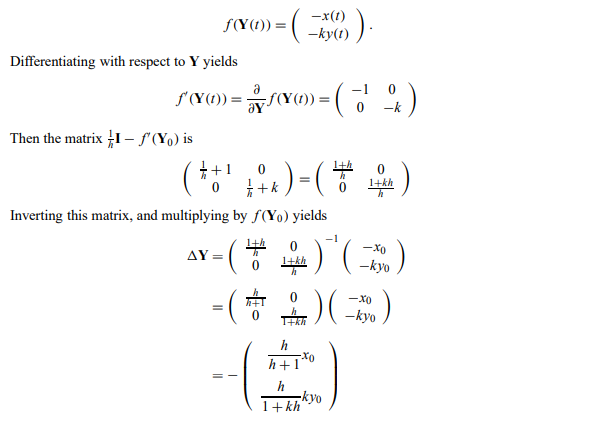
• 在这种情况下，步长的限制是多少？答案是：没有限制！在这种情况下，如果我们让h增长到无穷大，我们得到

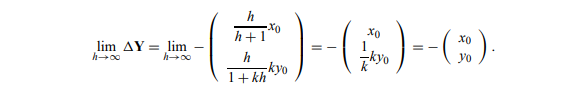
这意味着我们在一个步骤中实现了 Ynew = Y0 + （−Y0） = 0！对于一般的刚性 ODE，我们将无法采取任意大小的步骤，但是我们将能够使用隐式方法比使用显式方法采取更大的步骤。求解线性方程的额外成本通过采用大时间步长所节省的时间来弥补。