【ZJOI 2016】旅行者
题意
题解
大概是神题。
网格图上跑最短路有一个经典的优化方式:分治分组跑最短路。
对于这道题,设矩形长为 \(n\),宽为 \(m\),则对 \(n,m\) 中更大的一个二分。
这里只考虑按 \(n\) 分治的情况。
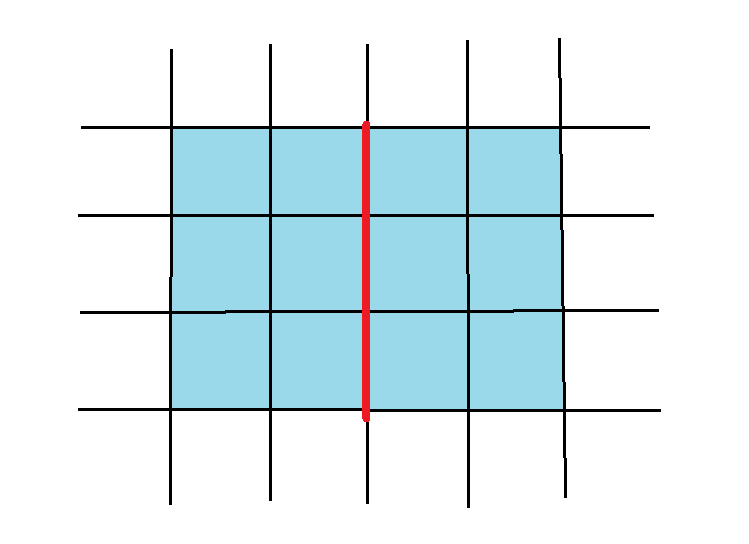
如上图,设 \(S=nm\),因为此时一列的点数是小等于 \(\sqrt{S}\) 的,所以我们可以枚举红色分割线上的点,以每个点为原点,跑到矩形中所有点的最短路。
然后考虑询问:
如果询问的两点在分割线的不同侧(或者至少有一端在分割线上),则最短路一定经过分割线,用分割线上的每个点到这两个点的最短距离之和更新答案,然后这个询问就不用管了。
如果询问的两点在分割线的同一侧,则最短路可能经过分割线,依然用分割线上的每个点到这两个点的最短距离之和更新答案,然后把这个询问扔到左/右递归区间,去寻找不经过分割线的最短路。
当然,有可能存在分割线上一点 到询问两端的最短路存在部分重合的情况。对于不同侧的情况,画图可知这种情况会被分割线上其它点 用更短路径覆盖掉;对于同一侧的情况,这种情况会被不经过分割线的更短路径覆盖掉。
时间复杂度 \(O(S\sqrt{S}\log^2{S})\)。嗯,码吧……
……
等等,你他吗说什么?这复杂度什么破玩意??跟 \(O(S^2)\) 有啥区别??你让我 \(2s\) 跑带大常数的 \(4e8\)???如果 cpu 是 I9 的说不定真能跑过
其实刚才这个复杂度是凭感觉意淫的,下面就是丧心病狂的算时间复杂度环节了
首先有 $$\begin{align} T(S)&=2T(\frac{S}{2})+O(S\sqrt{S}\log S) \nonumber \ &= T(S)=2T(\frac{S}{2})+O(S^{1.5}\log S) \nonumber \end{align}$$
然后参考这篇博客的主定理(这里有简单版)
假设我们有递归式 \(T(n)=aT(\frac{n}{b})+f(n)\),我们可以用主定理解这个递归式。
其中 \(n\) 为问题的规模,\(a\) 为递归到下一层的子问题数量,\(\frac{n}{b}\) 为每个子问题的规模,\(f(n)\) 为递推后做的额外计算。
本题中,\(a=b=2\),\(f(S)=O(S^{1.5}\log S)\)。
-
1. 假设存在常数 \(\epsilon>0\),使得 \(f(n)=O(n^{\log_b(a)-\epsilon})\),则 \(T(n)=\Theta(n^{log_ba})\)
\(\log_b a = \log_2 2 = 1\),则 \(S^{1-\epsilon}=S^{1.5}\log S\),显然 \(\epsilon<0\),故不符合主定理 1。 -
2. 假设存在常数 \(k\ge 0\),使得 \(f(n)=\Theta (n^{\log _{b}a}\log ^{k}n)\),则 \(T(n)=\Theta(n^{log_ba}\log^{k+1}n)\)。
\(S^{\log_b a}\log^k S = S\log^k S = S^{1.5}\log S\)
即要求 \(log^{k-1} S = S^{0.5}\)
参考具体数学第2版 p368 的渐进等级次序,可知 \(\log_x n\lt n^c\),其中 \(x\) 是任意 \(\gt 1\) 的底数,\(c\) 是任意 \(\gt 1\) 的指数,\(<\) 号重定义为函数的渐进增长率关系,即右边的函数更快到达无穷大。
比如有 \(\log n\lt n^{0.0001}\),这可能是很多人都不敢相信的,因为我们通常将视野局限于 \(n\) 不够大的情况,这种情况下 \(\log n\) 的值当然远大于 \(n^{0.0001}\)。比如 \(n=10^{100}\),\(\log n=100\),\(n^{0.0001}≈1.0233\)。但如果我们把 \(n\) 取到 \(10^{10^{100}}\),\(\log n\) 就小于 \(n^{0.0001}\) 了。
那把 \(\log_x n\) 取任意实数次幂,其增长速度是否还小于 \(n^c\) 呢?
确实是的。我们观察渐进增长率关系的定义:$$ f(n)<g(n) \rightleftharpoons \lim_{n \to \infty} \frac{f(n)}{g(n)}=0$$
显然对于任意实数 \(y\),都有 \(\frac{f(n)^y}{g(n)}=0\)。故二者的渐进增长率关系不变。
(这其实算是高数内容了,有点超纲,了解一下就好)
综上,\(log^{k-1} S = S^{0.5}\) 是不可能满足的,随着 \(S\) 的增长,二者的趋向无穷大的速度一定不同,只要 \(S\) 取得足够大,二者的取值就会不同。
故不符合主定理 2。 -
3. 假设存在常数 \(\epsilon >0\),有 \(f(n)=\Omega (n^{\log _{b}(a)+\epsilon })\),同时存在常数 \(c<1\) 以及充分大的 \(n\) 满足 \(af(\frac{n}{b})\le cf(n)\),那么 \(T\left(n\right)=\Theta \left(f\left(n\right)\right)\)。
其实前两个主定理都不符合了,那肯定是用主定理 3 算复杂度了……
本来想验证一下是否满足主定理 3 的,结果主定理 3 的那个 \(\Omega\) 我不会解啊 QvQ,哪位哥哥教教我
于是套用主定理 3,算得 \(T\left(n\right) = \Theta \left(f\left(n\right)\right) = \Theta (S\sqrt{S}\log S)\)。
所以时间复杂度是 \(\Theta (S\sqrt{S}\log S)\)(带不及 \(\log S\) 的小常数)……
这题有一个弱化版,就是强制 \(n\le 10^5\),\(m\le 10\),这时由于递归式里不带 \(\sqrt{S}\),要套主定理 2 而不是主定理 3,所以解出来的时间复杂度是 \(\Theta (mS\log m\log {S})\)。这就是双 \(\log\) 复杂度说法的来源……





