【BJOI2014/bzoj4530】大融合
题意
有 $n$ 个点,初始没有连边,要求支持两个动态操作:
1. 加一条边(保证之前两点不连通)
2. 查询过一条边的简单路径数量(就是两边连通块的大小的乘积)
$n,Q\le 100000$
题解
由第一个操作保证之前两点不连通的性质可知,$n$ 个点最多被连成一棵 $n-1$ 条边的生成树。
离线做法:树剖+树状数组/线段树
我们可以离线确定出最终森林的形态(我们给森林中的每棵树随便定义个根)。
然后重新模拟操作时,只需要在最终的森林上做一些链操作(统计答案用)。
由于只有加边操作,所以模拟加边时,用并查集维护连通树及当前连通树的根。
当前连通树的根就是在加一些边后,一个点所在连通树的深度最小的点,这个深度根据最终这棵树的形态而定,越靠近根深度越小。
同时我们还要维护当前以每个点为根的子树的大小。
这样,插入一条边时,假设在最终的树形态中 $u$ 是 $v$ 的父亲(这个是已知的,因为我们随便定了一个根),那我们在合并两个连通树时,把 $v$ 所在并查集连向 $u$ 所在并查集。
由于并查集只维护连通树的根,我们要把从 $u$ 到其所在连通树的当前根的所有点都更新子树大小。
画个图
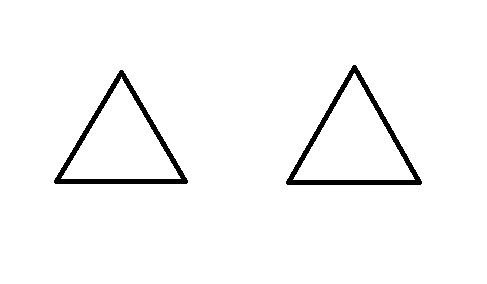
现在有一条边要连通如图两棵子树
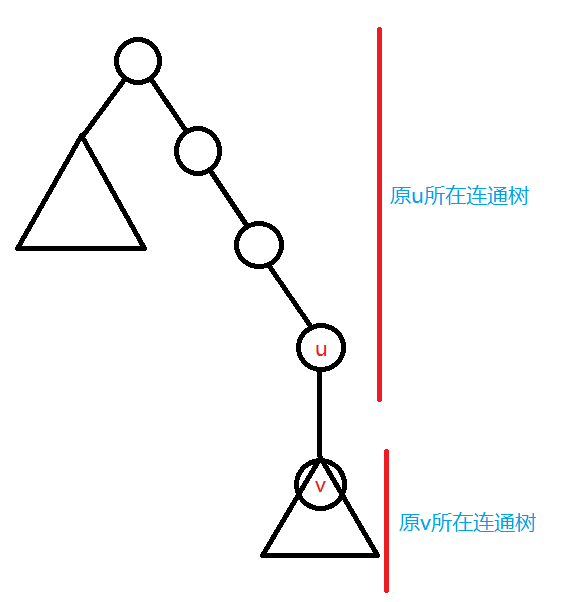
那么所有橙色点(即u到根的路径)都要更新子树大小
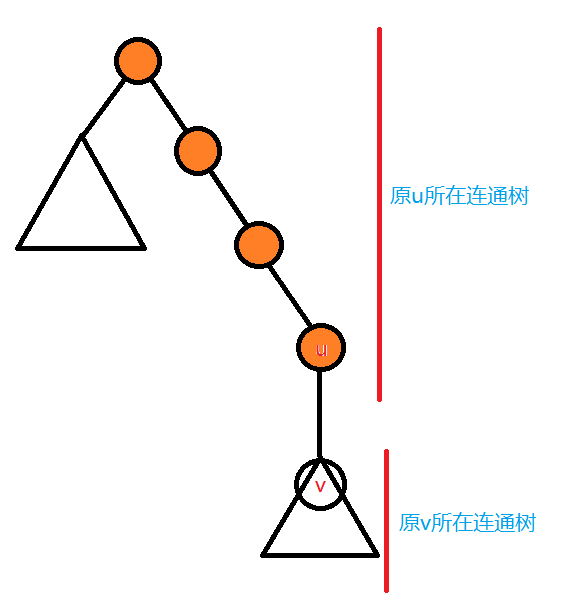
根据最终树的形态来确定 $u$、$v$ 的合并方向,就是为了在维护连通性的同时维护连通树的根。之前说过,连通树的根是 在树的最终形态中深度最小的点,如果 $u$ 是 $v$ 的父亲,那 $u$ 的深度当然比 $v$ 小,应该让 $v$ 的并查集连向 $u$ 的。
这样,我们实际上就是一边加边、一边维护每个点的子树大小。
加边不用实际加,只要连并查集就行了,因为在加边时,只有从其一端点 到它所在连通树的根 上的所有点要修改,路径的两端点都已知,直接树链剖分就行了。
查询……那两个点的子树 $size$ 都已知了,而且一个点还是另一个点的父亲,(设 $x$ 是 $y$ 的父亲,$rt$ 是 $x,y$ 两点所在连通树的根)答案就是 $size_y\times (size_{rt}-size_y)$。
$size_y$ 就是 $y$ 这边的点数,$size_{rt}-size_y$ 就是 $x$ 这边的点数。
画个图就是
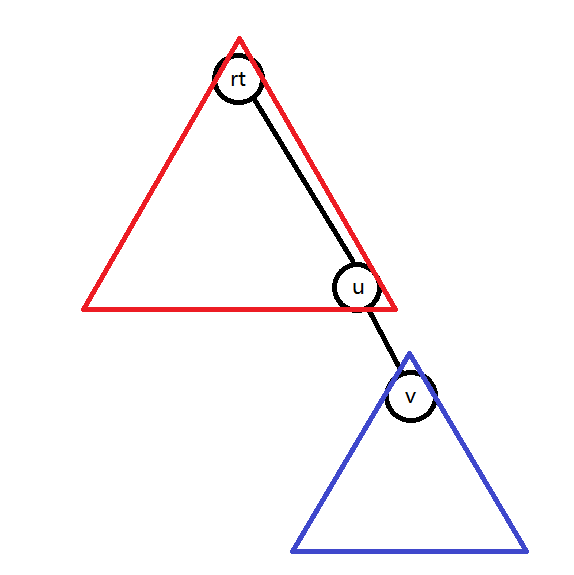
时间复杂度 $O(n + q\times log^2(n))$。
注:我没写这种方法,这是 $luogu$ 大佬的代码,其中的 $iota(f + 1, f + n + 1, 1);$ 就是 $for(int\space i=1;i<=n;++i)\space f[i]=i;$,即从 $1$ 开始以 $1$ 的斜率递增并依次赋值。

1 #include <cstdio> 2 3 #include <algorithm> 4 #include <numeric> 5 6 using namespace std; 7 8 struct edge { 9 int v; 10 edge* next; 11 }; 12 13 const int N = 100010; 14 15 int n; 16 char opt[N]; 17 int eu[N], ev[N], p[N], f[N], son[N], sum[N], fw[N], ord[N]; 18 int top[N]; 19 edge* g[N]; 20 21 int find(int x); 22 void add_edge(int u, int v); 23 void dfs1(int u); 24 void dfs2(int u); 25 void change(int k, int x); 26 void tchange(int u, int x); 27 int query(int k); 28 int low_bit(int k); 29 30 int main() { 31 int q; 32 scanf("%d%d", &n, &q); 33 for (int i = 1; i <= q; ++i) { 34 scanf(" %c%d%d", &opt[i], &eu[i], &ev[i]); 35 if (opt[i] == 'A') { 36 add_edge(eu[i], ev[i]); 37 add_edge(ev[i], eu[i]); 38 } 39 } 40 for (int u = 1; u <= n; ++u) 41 if (!p[u]) { 42 p[u] = -1; 43 dfs1(u); 44 } 45 for (int u = 1; u <= n; ++u) 46 if (p[u] == -1) { 47 top[u] = u; 48 dfs2(u); 49 } 50 iota(f + 1, f + n + 1, 1); 51 for (int i = 1; i <= n; ++i) { 52 tchange(i, 1); 53 tchange(p[i], -1); 54 } 55 for (int i = 1; i <= q; ++i) { 56 int u = eu[i], v = ev[i]; 57 if (p[u] == v) 58 swap(u, v); 59 int sv = query(ord[v]); 60 if (opt[i] == 'A') { 61 f[v] = find(u); 62 tchange(u, sv); 63 tchange(p[f[u]], -sv); 64 } else { 65 int s = query(ord[find(u)]); 66 printf("%d\n", (s - sv) * sv); 67 } 68 } 69 return 0; 70 } 71 72 void tchange(int u, int x) { 73 while (u != -1) { 74 change(ord[top[u]], x); 75 change(ord[u] + 1, -x); 76 u = p[top[u]]; 77 } 78 } 79 80 void dfs2(int u) { 81 static int t; 82 ord[u] = ++t; 83 if (!son[u]) 84 return; 85 top[son[u]] = top[u]; 86 dfs2(son[u]); 87 for (edge* q = g[u]; q; q = q->next) 88 if (p[q->v] == u && q->v != son[u]) { 89 top[q->v] = q->v; 90 dfs2(q->v); 91 } 92 } 93 94 int low_bit(int k) { 95 return k & -k; 96 } 97 98 void change(int k, int x) { 99 for (; k <= n; k += low_bit(k)) 100 fw[k] += x; 101 } 102 103 int query(int k) { 104 int ret = 0; 105 for (; k; k -= low_bit(k)) 106 ret += fw[k]; 107 return ret; 108 } 109 110 void dfs1(int u) { 111 sum[u] = 1; 112 for (edge* q = g[u]; q; q = q->next) 113 if (!p[q->v]) { 114 p[q->v] = u; 115 dfs1(q->v); 116 sum[u] += sum[q->v]; 117 if (sum[son[u]] < sum[q->v]) 118 son[u] = q->v; 119 } 120 } 121 122 int find(int x) { 123 return f[x] == x ? x : (f[x] = find(f[x])); 124 } 125 126 void add_edge(int u, int v) { 127 static edge pool[N * 2]; 128 static edge* p = pool; 129 p->v = v; 130 p->next = g[u]; 131 g[u] = p; 132 ++p; 133 }
在线做法:LCT
$LCT$ 由于使用 $splay$ 维护一条链,但 $splay$ 的中序遍历才是链从上往下的顺序,形态不一样(同一点在 $splay$ 的子树和在原树中的子树也不一样),所以 $splay$ 没法直接维护原树的子树信息。
但对于某些题来说,可以做一些“假的”维护子树信息。
对于这题,即使询问边的两端点 $x,y$ 是相邻的,我们也可以 $split$ 出 $x$ 到 $y$ 的只有一条边的路径。
这里复习一下 $split(x,y)$ 是干嘛来着。
首先 $makeroot(x)$,即 $x$ 成了其所在 $splay$ 的根,且它没有左子树。
然后 $access(y)$,由于 $x$ 和 $y$ 本来就相邻,那么两点间就连了条重边,两点连出的其余所有边都变成轻边。
最后 $splay(y)$,$y$ 成了这个 $splay$ 的根,$x$ 成了 $y$ 的左儿子 且 $x$ 没有儿子。
也就是说,$split(x,y)$ 后,就成了这样子
那这俩点所在的 $splay$ 就只剩这 $2$ 个点了!(详见 $access$)
而且两点连出去的其它边都是轻边!
我们知道,轻边不是用 $splay$ 维护的,所以我们可以 $fake$ 一下,装作维护子树信息,其实是维护每个点的所有轻儿子的子树信息。
轻儿子的信息分这么几个部分维护:
1. 做某些操作时,对于一个点的所有儿子,一条边变重后,原来的重边变成轻边,所以这个点的轻子树大小总和 $lit$ 减去变重的儿子的 $size$,加上变轻的儿子的 $size$。
2. 加边时($link(x,y)$),由于 $split(x,y)$,$y$ 会变成 $x$ 的父亲,且两点间连上重边,所以 $y$ 的 $lit$ 加上 以 $x$ 为根的子树的 $size$。
3. $splay$ 做 $pushup$ 时别忘了把 $size$ 值加上其 $lit$。本来 $LCT$ 的 $splay$ 是不维护轻子树信息的,这里为了最后的查询,可以直接加上它们(比较方便)。
查询时,实际上就是查询 $x$ 的所有轻儿子的子树大小总和。由于 $x$ 没有重儿子,它的 $size$ 值实际上就是它本身和所有轻子树大小的总和,也就是 $x$ 这边的答案。
$y$ 那边的答案就是 $size_y-size_x$。
原来这类题还可以直接把 $size$ 加上轻儿子的信息……
最后说一个我做题时混淆了的概念:
如果连一条边会影响一端点及其所有祖先的信息(比如子树 $size$ 值,连边时就会影响点 $y$ 及其所有祖先),那 $link(x,y)$ 时不能只 $makeroot(x)$(把 $x$ 设成其所在的树的根,然后修改其父亲为 $y$,$y$ 的位置其实无所谓),而要 $split$ 出这两点的路径(也就是说要把 $y$ 转到整棵树根)。
因为 $LCT$ 只保证了每棵 $splay$ 的深度是 $log$ 级别的,没有保证整棵树的深度,也就是说如果不把 $y$ 设成根,把 $y$ 一直 $pushup$ 到整棵树的根等于做暴力,复杂度不对。
时间复杂度 $O(n+q\times log(n))$。

1 #include<bits/stdc++.h> 2 #define rep(i,x,y) for(int i=x;i<=y;++i) 3 #define dwn(i,x,y) for(int i=x;i>=y;--i) 4 #define ll long long 5 #define N 100002 6 using namespace std; 7 inline int read(){ 8 int x=0; bool f=1; char c=getchar(); 9 for(;!isdigit(c);c=getchar()) if(c=='-') f=0; 10 for(; isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+(c^'0'); 11 if(f) return x; 12 return 0-x; 13 } 14 int n,m,siz[N],son[N][2],fa[N],lit[N]; //lit维护一个点的所有轻边连向的子树 15 bool rev[N]; 16 namespace LCT{ 17 inline bool dir(int x){return son[fa[x]][1]==x;} 18 inline bool isroot(int x){return son[fa[x]][0]!=x && son[fa[x]][1]!=x;} 19 inline void pushup(int x){siz[x]=siz[son[x][0]]+siz[son[x][1]]+lit[x]+1;} 20 inline void pushdown(int x){ 21 if(rev[x]) 22 swap(son[x][0],son[x][1]), rev[son[x][0]]^=1, rev[son[x][1]]^=1, rev[x]=0; 23 } 24 inline void rotate(int x){ 25 int f,ff,k; f=fa[x],ff=fa[f],k=dir(x); 26 fa[x]=ff; if(!isroot(f)) son[ff][dir(f)]=x; 27 son[fa[son[x][k^1]]=f][k] = son[x][k^1]; 28 son[fa[f]=x][k^1]=f; 29 pushup(f), pushup(x); 30 } 31 inline void splay(int x){ 32 int sta[N],top,f; 33 for(int i=x,top=0;!isroot(i);i=fa[i]) sta[top--]=i; 34 for(;top;pushdown(sta[--top])); 35 for(f=fa[x];!isroot(x);rotate(x),f=fa[x]) 36 if(!isroot(f)) rotate(dir(f)==dir(x)?f:x); 37 } 38 inline void access(int x){ 39 for(int s=0,f=x; f; s=f,f=fa[f]){ 40 splay(f); 41 lit[f]+=siz[son[f][1]]-siz[s]; //f与s间连上了重边,与原来f的重儿子(即splay中f的右儿子)连上了轻边,由于是维护轻子树信息,所以要加一个、减一个。 42 //printf("%d %d %d\n",s,f,lit[f]); 43 if(lit[f]<0) printf("err\n"); 44 son[f][1]=s, pushup(f); 45 } 46 } 47 inline void makeroot(int x){access(x),splay(x),rev[x]^=1;} 48 inline void split(int x,int y){makeroot(x),access(y),splay(y);} 49 inline void link(int x,int y){split(x,y),fa[x]=y; lit[y]+=siz[x],pushup(y);} 50 inline ll query(int x,int y){split(x,y); return 1ll*siz[x]*(siz[y]-siz[x]);} 51 } 52 using namespace LCT; 53 int main(){ 54 n=read(),m=read(); 55 rep(i,1,n) siz[i]=1; 56 char opt[2]; int x,y; 57 rep(i,1,m){ 58 scanf("%s",opt); x=read(),y=read(); 59 if(opt[0]=='A') link(x,y); 60 else printf("%lld\n",query(x,y)); 61 } 62 return 0; 63 }




